关于OpenCV的那些事——相机标定

这一节我们首先介绍下计算机视觉领域中常见的三个坐标系：图像坐标系，相机坐标系，世界坐标系。以及他们之间的关系。然后介绍如何使用张正友相机标定法标定相机。

图像坐标系：

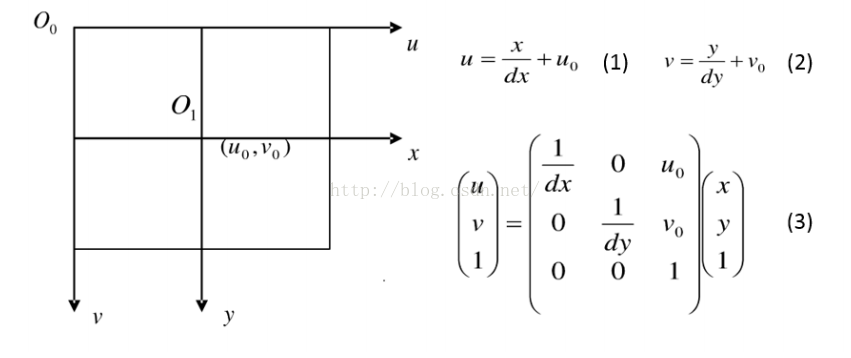
理想的图像坐标系原点O1和真实的O0有一定的偏差，由此我们建立了等式（1）和（2），可以用矩阵形式（3）表示。

相机坐标系（C）和世界坐标系（W）：

通过相机与图像的投影关系，我们得到了等式（4）和等式（5），可以用矩阵形式（6）表示。我们又知道相机坐标系和世界坐标的关系可以用等式（7）表示：

由等式（3），等式（6）和等式（7）我们可以推导出图像坐标系和世界坐标系的关系：

其中M1称为相机的内参矩阵，包含内参（fx，fy，u0，v0）。M2称为相机的外参矩阵，包含外参（R:旋转矩阵，T:平移矩阵）。

众所周知，相机镜头存在一些畸变，主要是径向畸变（下图dr），也包括切向畸变（下图dt）等。

上图右侧等式中，k1,k2,k3,k4,k5,k6为径向畸变，p1,p2为切向畸变。在OpenCV中我们使用张正友相机标定法通过10幅不同角度的棋盘图像来标定相机获得相机内参和畸变系数。函数为calibrateCamera(objectPoints, imagePoints, imageSize, cameraMatrix, distCoeffs, rvecs, tvecs，flag)

objectPoints: 一组世界坐标系中的3D

imag