支持向量机SVM的训练过程中需要求解带约束的最优化问题。
带约束的最优化问题通常表述如下:
objective:minw f(w)s.t. {gi(w)≤0,hj(w)=0,i=1,2,3...n;j=1,2,3...m;不等式约束等式约束 o b j e c t i v e : min w f ( w ) s . t . { g i ( w ) ≤ 0 , i = 1 , 2 , 3... n ; 不等式约束 h j ( w ) = 0 , j = 1 , 2 , 3... m ; 等式约束
gi(w) g i ( w ) , hj(w) h j ( w ) 和 f(w) f ( w ) 一般都是连续可导的。要求在满足 gi(w)≤0,hj(w)=0 g i ( w ) ≤ 0 , h j ( w ) = 0 的前提下求能使得目标函数 f(w) f ( w ) 最小化的 w w 。
学习支持向量机SVM时,拉格朗日对偶、Slater条件、KKT条件等一大堆概念席卷而来,让没系统学习过凸优化的笔者一头雾水,估计不少人都是这样吧。
不幸的是笔者在数学相关问题上经常一不小心就陷入死磕,遇到没想明白的问题就总惦记着。另外笔者还是个懒于动手的人,但好在数学是一门完全不需要动手的学科,你只要靠想就可以,最多需要在纸上画画,完全不用做什么实验或者手工体力活儿,嗯,很适合笔者这种懒人,这也是笔者为什么从一个电气工程学生慢慢偏离航向发展成一个程序猿的原因。
回到我们要说的SVM中的优化问题。为什么要引入一堆系数把约束条件与目标函数组合到一起?为什么满足了KKT条件就是符合条件的解? 为什么可以转化为对偶问题?什么是Slater条件?在讲SVM的资料中通常不会详细展开这些问题,只是告知读者有这么回事。带着一排排问号,翻阅文献、Wiki、博客,加上自己的一些思考,算是把不少问题整理清楚了。笔者希望能把这些问题用容易理解的方式讲述明白,通过这一系列博文,将相关问题由易到难一一做出解释,希望这个系列的文章能帮更多人解惑。
本系列文章包括:
1. 纯等式约束时的optimalize问题
2. 纯不等式约束时的optimalize问题
3.混合约束时的optimalize问题——KKT条件与拉格朗日对偶问题
4.强对偶性的证明与Slater条件
1. 纯等式约束时的optimalize问题
这一类问题的范式如下:
在满足 hj(w)=0 h j ( w ) = 0 的条件下使 f(w) f ( w ) 最小化。 hj(w) h j ( w ) 和 f(w) f ( w ) 都应是连续可导的。上面纯代数的形式会让人不容易看到此类问题的本质,我们希望对这类问题有一个直观的几何理解。首先我们来看一下每个等式约束的含义。
等式约束的几何意义
对于
hj(w)=0
h
j
(
w
)
=
0
,如果
w
w
是一个3维变量,那所有满足的
w
w
点集通常会组成一个 2 维的曲面。特别当是
w
w
的线性函数时,比如 :
其中 wx、wy、wz w x 、 w y 、 w z 分别是w w 在三个维度上的分量,a1、a2、a3、b是某些常数。这时 hj(w)=0 h j ( w ) = 0 就是三维空间中的一个平面。对于通常的非线性函数而言, hj(w)=0 h j ( w ) = 0 一般对应一个曲面。
如果w w 是更高维的变量,维数设为dw,那hj(w)=0 h j ( w ) = 0 一般对应一个(dw−1) ( d w − 1 ) 维的子空间,或者说(dw−1) ( d w − 1 ) 维的曲面。注意,当我们下面再提到”面”这个概念时,它不一定代表狭义的二维面,而可以是对任意维度的一个子空间的称谓。
借用下物理中的概念:如果将hj(w) h j ( w ) 看做空间中某个向量场的势函数,这个向量场就是hj(w) h j ( w ) 的梯度场∇hj(w) ∇ h j ( w ) ,而hj(w)=0 h j ( w ) = 0 所对应的子空间就是该梯度场的0等势面。在等势面上任一点的梯度都与该点邻域内的等势面垂直,即若w∗ w ∗ 是等势面上一点,则∇hj(w∗) ∇ h j ( w ∗ ) 垂直于该等势面。(通常等势面是个曲面,当我们说垂直的时候,只是针对该面上某个点的切面)
进一步的,c∇hj(w∗) c ∇ h j ( w ∗ ) 构成了一个1维的子空间Gj G j ,这个子空间与(dw−1) ( d w − 1 ) 维的0等势面(在w∗ w ∗ 处的切面)垂直,因此它们互为补空间(相互垂直且维度之和是dw d w )。这意味着,在w∗ w ∗ 处所有与0等势面垂直的向量都在Gj G j 子空间中,即都可表示成一个常数与∇hj(w∗) ∇ h j ( w ∗ ) 相乘。
继续往下读之前先确保理解了上面几段的内容。提示:在本文中遇到高维相关结论,可以先在大脑里以我们熟悉的三维空间举例理解。
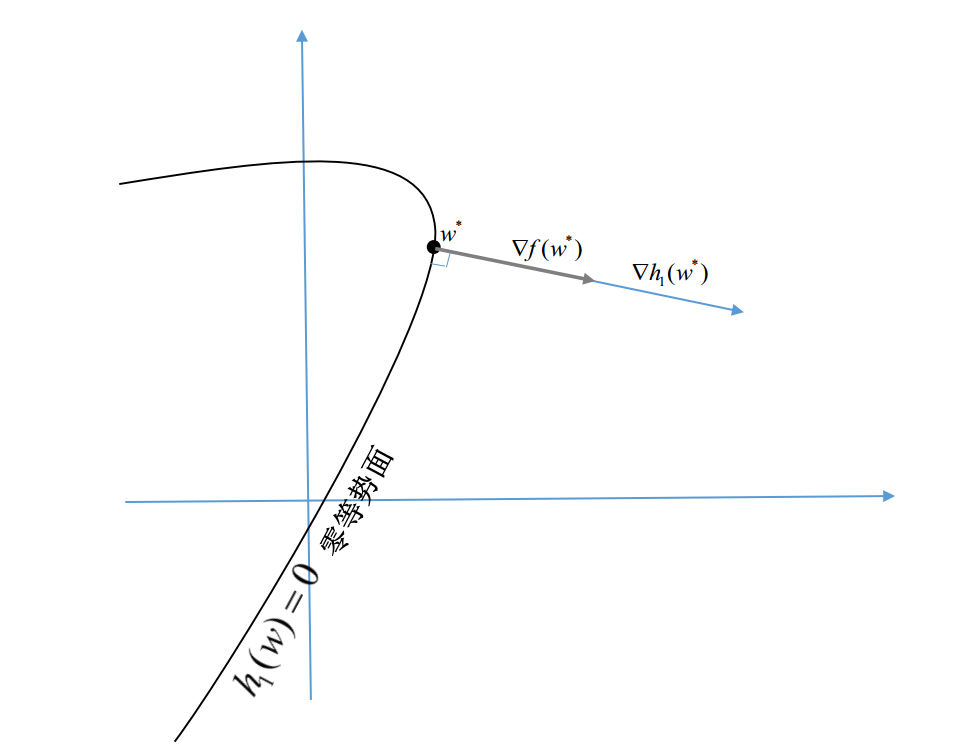
再回到我们的问题,这里我们有m个等式约束,每个约束都对应一个0等势面,m个约束同时作用,相当于把可行域限制在了这m个0等势面的交集上。这个交集是什么样子?它也是一个子空间,只不过维数可能更低。比如三维空间中两个不平行的面(2维)的交集,是一条1维的线。我们先称呼前面提到的这个交集为”公共0势面”。
假设公共0势面的维度是d0 d 0 ,通常d0=dw−m d 0 = d w − m 。而各hj(w) h j ( w ) 在公共0势面上某点w∗ w ∗ 处的梯度向量∇hj(w∗) ∇ h j ( w ∗ ) 都与公共0势面垂直,且共有m个这样的向量,因此这些梯度向量组合成的m维子空间G G 与公共0势面互补。意味着:w∗处所有与公共0势面垂直的向量都在G G 子空间中,即都可表示成:
V=m∑j=1cj∇hj(w∗)
当然,d0 d 0 也有大于dw−m d w − m 的时候,但这并不影响上面的结论。假如m个等势面中有某(t+1) ( t + 1 ) 个等势面是相切的,这时公共等势面变成了dw−(m−t) d w − ( m − t ) 维,比正常时候多了t个维度;但另一方面,梯度空间G也会因此而减少t个维度,因为有(t+1) ( t + 1 ) 个梯度是平行的,它们只能提供1个维度。此时,上面的结论保持不变
公共0势面上的极值条件
我们已经知道,满足所有等式约束的点,都在前面提到的公共0势面上。那我们的目标函数f(w)
f
(
w
)
的极值点怎么找呢?
通常,在没有约束的时候,我们要找f(w)
f
(
w
)
的极值点,只要找f(w)
f
(
w
)
梯度为0的点,即∇f(w)
∇
f
(
w
)
是0。而我们把可行域限制在公共0势面上之后呢?对,我们只要要求梯度向量∇f(w)
∇
f
(
w
)
在公共0势面上的分量为0即可,换句话说,梯度向量与公共0势面垂直。
为了表达具体一点我们不得不把倒霉的w∗
w
∗
再抓回来当我们的小白鼠。我们继续把它在公共0势面上,看一下它怎样才能变成极值点。
我们要求f(w)
f
(
w
)
在w∗
w
∗
处的梯度向量∇f(w∗)
∇
f
(
w
∗
)
与该处的公共0势面垂直,意味着∇f(w∗)
∇
f
(
w
∗
)
必然在前面提到的梯度子空间G上,即它可以由各个等式约束函数在w∗
w
∗
处的梯度线性组合而成,即存在一系列系数βj
β
j
,满足下式:
∇f(w∗)+m∑j=1βj∇hj(w∗)=0
这就是判定 w∗ w ∗ 是否是可行域内极值点的方法。
结论
当我们求解纯等式约束下的最优化问题时,我们只需求解如下方程组即可求得候选解,然后从中挑选最优解:
求解w和β{∇f(w)+∑mj=1βj∇hj(w)=0hj(w)=0for j=1,2...m
或者我们可以构造一个能把约束条件与目标函数融合到一起的新函数:
L(w,β)=f(w)+m∑j=1βjhj(w)
不错,狡猾的笔者偷偷把 拉格朗日乘子式的雏形列了出来,就在读者察觉到怎么读了这么久还没看到拉格朗日大人的踪影是不是走错片场了的时候。
这时,上面的方程组其实就是
求解w和β{∂L∂wk=0for k=1,2,3...dw(w的维数)∂L∂βj=0for j=1,2...m
多说两句,这个方程组中共有 (dw+m) ( d w + m ) 个未知量和方程。
其中 ∂L∂wk=0 ∂ L ∂ w k = 0 是同时包含 w,β w , β 的方程,这样的方程共有 dw d w 个;
而 ∂L∂βj=hj(w)=0 ∂ L ∂ β j = h j ( w ) = 0 是只包含 w w 的方程,这样的方程共有m个。为使w有解,m应小于 w w 的维数dw,否则对 w w 的约束方程数将大于w的变量个数导致约束太强、各约束方程无法同时被满足而无解;
因此当d>m d > m 时,上面的方程组通常是有解的。特别是当目标函数f(w) f ( w ) 是w w 的二次函数、hj(w)都是w的一次函数即仿射函数时,上面的方程组就变了一个线性方程组,可以用线性代数方法直接求解
简单解释一下:
当f(w) f ( w ) 是w w 的二次函数、hj(w)是w w 的一次函数时,他们对wk的偏导分别是w w 的一次和零次(常数)函数,所以他们的组合函数 L(w,β)对wk w k 的偏导∂L∂wk ∂ L ∂ w k 就是w,β w , β 的一次函数,∂L∂wk=0 ∂ L ∂ w k = 0 就是一个线性方程;
而∂L∂βj=0 ∂ L ∂ β j = 0 等价于hj(w)=0 h j ( w ) = 0 ,hi(w) h i ( w ) 是w w 的一次函数,因此所有的hj(w)=0也都是线性方程;
于是整个方程组就变成了线性方程组
一句话概括
求解等式约束下的最优化问题,只需要解个方程组就可以找到候选极值点,然后在方程组的各个解中筛选出满足条件的最小值点即可(该方程组有可能是多解的)。
如果目标函数是二次函数,且约束都是线性的,那我们只需要求解一个线性方程组。
2. 纯不等式约束时的optimalize问题
这一类问题的范式如下:
objective:minw f(w)s.t:gi(w)≤0,i=1,2,3...n;
gi(w) g i ( w ) 和f(w) f ( w ) 都应是连续可导的。为了方便理解,我们先看只有一个不等式约束时的情形
只有一个不等式约束的情况
objective:minw f(w)s.t:g1(w)≤0
对于某个给定的 w∗ w ∗ ,如果它在可行域的内部,即 g1(w∗)<0 g 1 ( w ∗ ) < 0 时,只需判断 f(w) f ( w ) 在 w∗ w ∗ 处的梯度 ∇f(w∗) ∇ f ( w ∗ ) 是否为0即可判断其是否是可行域上的候选极值点。
而如果 w∗ w ∗ 在可行域的边界,即 g1(w)=0 g 1 ( w ) = 0 时,情况就稍微复杂。首先,我们要保证至少在边界面上, w∗ w ∗ 是一个极值点(条件一);其次,还要保证在可行域内部, w∗ w ∗ 的邻域内的其他点的函数值都比 f(w∗) f ( w ∗ ) 大(条件二)。
为满足条件一, ∇f(w∗) ∇ f ( w ∗ ) 在边界面上的梯度分量应为0,即 ∇f(w∗) ∇ f ( w ∗ ) 与边界面垂直。而边界面其实是 g1(w) g 1 ( w ) 的零等势面,因此 ∇g1(w∗) ∇ g 1 ( w ∗ ) 也垂直于边界面。这样 ∇f(w∗) ∇ f ( w ∗ ) 就应与 ∇g1(w∗) ∇ g 1 ( w ∗ ) 平行,即 ∇f(w∗)+α1∇g1(w∗)=0
但这还不够,我们还要考虑不在边界上的内点。设 (w∗+Δw) ( w ∗ + Δ w ) 是邻域内任一点,则当 Δw Δ w 满足如下条件时:(注意 Δw Δ w 与梯度一样都是向量,而非标量) ∇g1(w∗)⋅Δw≤0
(w∗+Δw) ( w ∗ + Δ w ) 就是可行域上的点,因为这时满足 g1(w∗+Δw)=g1(w∗)+∇g1(w∗)⋅Δw≤0 g 1 ( w ∗ + Δ w ) = g 1 ( w ∗ ) + ∇ g 1 ( w ∗ ) ⋅ Δ w ≤ 0 。
为使 f(w) f ( w ) 能在 w∗ w ∗ 处取可行域上的极小值,对于可行域内的所有 Δw Δ w 须满足 ∇f(w∗)⋅Δw≥0 ∇ f ( w ∗ ) ⋅ Δ w ≥ 0 ,即
−α1∇g1(w∗)⋅Δw≥0
而 ∇g1(w∗)⋅Δw≤0 ∇ g 1 ( w ∗ ) ⋅ Δ w ≤ 0 ,因此此时 α1≥0 α 1 ≥ 0 。
从几何角度来说,上面的两个条件对应的意义是:∇f(w∗) ∇ f ( w ∗ ) 应与边界面垂直并指向包含可行域的一侧(边界面的一侧包含可行域,另一侧不包含可行域)。函数值沿着梯度方向是增长的,当f(w) f ( w ) 在w∗ w ∗ 处的梯度指向可行域一侧时,可行域内部的函数值都比w∗ w ∗ 处大,w∗ w ∗ 才能是极小点
现在可以做个小结了:若w∗
w
∗
是可行域上的极值点,则应满足:
{∇f(w∗)+α1∇g1(w∗)=0且α1≥0w∗是边界点,即g1(w∗)=0时∇f(w∗)=0w∗是内点,即g1(w∗)<0时
或者换一种更统一的形式
∇f(w∗)+α1∇g1(w∗)=0其中α1≥0,且当g1(w∗)<0时只能取等号
我们甚至可以把原问题中的约束条件也包进来,构造一个完整的方程组:
求解w和α1{∇f(w)+α1∇g1(w)=0α1g1(w)=0α1≥0, g1(w)≤0
巧妙的是,第二行的(α1g1(w)=0) ( α 1 g 1 ( w ) = 0 ) 和第三行的(α1≥0, g1(w)≤0) ( α 1 ≥ 0 , g 1 ( w ) ≤ 0 ) 联合起来,正好暗示了一个规则:当g1(w)<0 g 1 ( w ) < 0 时,α1=0 α 1 = 0 ;只有当g1(w)=0 g 1 ( w ) = 0 时,α1 α 1 才可能大于0
同时存在多个不等式约束的情况
objective:minw f(w)s.t:gi(w)≤0,i=1,2,3...n;
多个不等式约束同时存在时,思路与前面大致相同。
如果 w∗ w ∗ 不在边界上,只需判断 ∇f(w∗) ∇ f ( w ∗ ) 是否为0;
如果 w∗ w ∗ 只在其中某一个约束比如 gi(w)≤0 g i ( w ) ≤ 0 的边界上,处理方法与前面一样;
唯一需要多加考虑的,是当 w∗ w ∗ 同时在多个约束的公共边界上的情况,即 w∗ w ∗ 在多个不同约束的边界面的交集上,比如, g1(w∗)=g2(w∗)=g3(w∗)=g4(w∗)=0 g 1 ( w ∗ ) = g 2 ( w ∗ ) = g 3 ( w ∗ ) = g 4 ( w ∗ ) = 0 。下面以此为例来说明。
首先,为使 w∗ w ∗ 在公共边界上满足极值条件, ∇f(w∗) ∇ f ( w ∗ ) 应与公共边界垂直。
而公共边界同时属于 g1(w∗)、g2(w∗)、g3(w∗)、g4(w∗) g 1 ( w ∗ ) 、 g 2 ( w ∗ ) 、 g 3 ( w ∗ ) 、 g 4 ( w ∗ ) 的0等势面,因此 ∇g1(w∗)、∇g2(w∗)、∇g3(w∗)、∇g3(w∗) ∇ g 1 ( w ∗ ) 、 ∇ g 2 ( w ∗ ) 、 ∇ g 3 ( w ∗ ) 、 ∇ g 3 ( w ∗ ) 分别都与公共边界垂直,且这四个向量张成的四维空间正好构成公共边界的补空间,所有与公共边界垂直的向量,都在这个补空间中,可以被这四个向量的线性组合表示。
因此 ∇f(w∗)+4∑i=1αi∇gi(w∗)=0
同样,我们还要关心可行域上、公共边界以外的其他点。
设 (w∗+Δw) ( w ∗ + Δ w ) 是邻域内任一点,当 Δw Δ w 同时满足如下条件时:
∇gi(w∗)⋅Δw≤0,其中i=1,2,3,4
(w∗+Δw) ( w ∗ + Δ w ) 就是可行域上的点。
为使 f(w) f ( w ) 能在 w∗ w ∗ 处取可行域上的极小值,对于可行域内的所有 Δw Δ w 须满足 ∇f(w∗)⋅Δw≥0 ∇ f ( w ∗ ) ⋅ Δ w ≥ 0 ,即
−4∑i=1αi∇gi(w∗)⋅Δw≥0
同样的几何意义:∇f(w∗) ∇ f ( w ∗ ) 应与公共边界面垂直并指向靠近可行域的方向。
这里说的“靠近可行域的方向”,是指与可行域夹角小于等于90°的方向。准确的说,对于所有能使(w∗+Δw) ( w ∗ + Δ w ) 位于可行域上的微小位移向量 Δw Δ w ,与∇f(w∗) ∇ f ( w ∗ ) 夹角都应小于等于90°,用内积表示就是∇f(w∗)⋅Δw≥0 ∇ f ( w ∗ ) ⋅ Δ w ≥ 0
结合∇gi(w∗)⋅Δw≤0 ∇ g i ( w ∗ ) ⋅ Δ w ≤ 0 ,为保证对所有满足的条件的Δw Δ w 上式都能成立,必须要求每个αi α i 都大于等于0。
否则,假如α1 α 1 小于0,对于满足以下条件Δw Δ w ,∇g1(w∗)⋅Δw<0, ∇g2(w∗)⋅Δw=0,∇g3(w∗)⋅Δw=0, ∇g4(w∗)⋅Δw=0
∇ g 1 ( w ∗ ) ⋅ Δ w < 0 , ∇ g 2 ( w ∗ ) ⋅ Δ w = 0 , ∇ g 3 ( w ∗ ) ⋅ Δ w = 0 , ∇ g 4 ( w ∗ ) ⋅ Δ w = 0上面的式子就不成立了
总结起来就是,当w∗
w
∗
在上述公共边界并是可行极值点时,应满足:
∇f(w∗)+n∑i=1α1∇g1(w∗)=0仅当i=1,2,3,4时,αi≥0,其他αi=0
OK,有了这个特例的辅助,我们很容易将结论一般化如下:
∇f(w∗)+n∑i=1α1∇g1(w∗)=0其中αi≥0,且当gi(w∗)<0,即w∗不在第i个约束边界时必须取等号
我们继续运用前面说到的巧妙办法,把原问题中的约束条件也包进来,构造一个完整的方程组:
求解w和α{∇f(w)+∑ni=1αi∇gi(w)=0αigi(w)=0for i=1,2...nαi≥0, gi(w)≤0for i=1,2...n
现在到再请出拉格朗日大人的时候了。我们构造一个能把约束和目标函数融合在一起的新函数,如下(拉格朗日乘子式):
L(w,α)=f(w)+n∑i=1αigi(w)
这时上面的方程组变成了
求解w和α{∂L∂wk=0for k=1,2,3...dw(w的维数)αi⋅∂L∂αi=0for i=1,2...nαi≥0,∂L∂αi≤0for i=1,2...n
这里共有 dw+n d w + n 个等式方程和 dw+n d w + n 个变量,可以先求解前两行构成的等式方程组,再排除掉其中不符合第三行条件的解,剩下的即是符合条件候选极值点。
然而,第二行的方程与纯等式约束时的情况不太一样,纯等式约束下只要求约束式的偏导为0,而这里是要求偏导与系数(也是待求的未知数)乘积为0,这增加了解方程的难度。即便当目标函数是二次的、不等式约束都是线性的时候,方程组整体也变成了二次方程组,很难直接求解。不过,这时不等式约束的数量n是可以大于d_w的,因为第二行的方程不在只包含 w w ,同时也包含了α,不会出现 w w 的约束太强而无解。
3. 混合约束时的optimalize问题——KKT条件与拉格朗日对偶问题
这一类问题的范式如下:
objective:minw f(w)s.t. {gi(w)≤0,i=1,2,3...n;不等式约束hj(w)=0,j=1,2,3...m;等式约束
gi(w) g i ( w ) , hj(w) h j ( w ) 和 f(w) f ( w ) 都应是连续可导的。
拉格朗日乘子式与KKT条件
有了前面纯等式和纯不等式约束问题的铺垫,我们可以轻松得出混合约束时的结论。
首先,还是先考虑最简单的情况,假如w∗
w
∗
不在任何不等式的边界,即gi(w∗)<0
g
i
(
w
∗
)
<
0
对所有 i=1,2...n
i
=
1
,
2...
n
成立。——被玩坏的w∗
w
∗
肯定在抱怨:为什么又是我躺枪,隔壁w′
w
′
闲了两天了!但显然无情的笔者才不打算关心这个声音。
但w∗
w
∗
须仍在所有等式约束hj(w)
h
j
(
w
)
的公共0势面上。这时相当于只有等式约束,w∗
w
∗
是极值的条件是:
∇f(w∗)+m∑j=1βj∇hj(w∗)=0
我们再把w∗
w
∗
扔到不等式的边界上看看会发生什么。有了之前纯不等式约束的基础,我们直接考虑w∗
w
∗
同时在多个不等式约束边界时的情况,假如w∗
w
∗
在第1、2、3、4个不等式约束的公共边界面上,即:
{gi(w∗)=0for i=1,2,3,4gi(w∗)<0for i=otherhj(w∗)=0for j=1,2...m
可见,这个公共边界面,属于 g1(w)、g2(w)、g3(w)、g4(w) g 1 ( w ) 、 g 2 ( w ) 、 g 3 ( w ) 、 g 4 ( w ) 和 h1(w)、h2(w)...hm(w) h 1 ( w ) 、 h 2 ( w ) . . . h m ( w ) 的公共混合0势面的一部分。如果想让 f(w) f ( w ) 在 w∗ w ∗ 处是可行域上的一个极值,首先要保证 w∗ w ∗ 在这个公共混合0势面上是极值,即 f(w) f ( w ) 在 w∗ w ∗ 处的梯度应垂直于该混合0势面,可以表示成:
∇f(w∗)+m∑j=1βj∇hj(w∗)+4∑i=1αi∇gi(w∗)=0
但这还不够,为了保证可行域上w∗ w ∗ 所有邻域点(w∗+Δw) ( w ∗ + Δ w ) 的目标函数值都比w∗ w ∗ 处大,α1...α4 α 1 . . . α 4 还应都是大于等于0的,具体分析过程与讲解纯不等式约束问题时类似,不再重复。
再强调下几何意义:∇f(w∗) ∇ f ( w ∗ ) 应与公共混合0势面垂直并指向靠近可行域的方向。
将上面两种情况用统一的形式重写如下,w∗
w
∗
是可行域上极值点的条件是:
∇f(w∗)+m∑j=1βj∇hj(w∗)+n∑i=1α1∇g1(w∗)=0其中αi≥0,且当gi(w∗)<0,即w∗不在第i个不等式约束边界时只能取等号
因此,我们可以通过解以下方程组(前3行等式构成方程组)
求解w、α和β{∇f(w)+∑mj=1βj∇hj(w)+∑ni=1αi∇gi(w)=0hj(w)=0for j=1,2...mαigi(w)=0for i=1,2...nαi≥0,gi(w)≤0for i=1,2...n
然后排除掉不满足第4行的解,就可以得到可行域上的候选极值点。
然后,拉格朗日时间到。是时候引出完整版的拉格朗日乘子式了,我们构造一个融合目标函数和所有约束的新函数:
L(w,α,β)=f(w)+n∑i=1αigi(w)+m∑j=1βjhj(w)
然后前面的方程组就变成了
求解w、α和β{∂L∂wk=0for k=1,2,3...dw(w的维数)∂L∂βj=0for j=1,2...mαi⋅∂L∂αi=0for i=1,2...nαi≥0,∂L∂αi≤0for i=1,2...n
是的,我们就这样得到了广为流传的KKT条件。对于某组给定的(w∗,α∗,β∗) ( w ∗ , α ∗ , β ∗ ) ,如果能同时满足上面的条件,w∗ w ∗ 就是原问题的候选解,但候选解不一定是最优解。KKT条件只是最优解的必要条件。
拉格朗日对偶问题
前面KKT条件中的方程组通常是很难直接求解的。而有些时候,将原问题转换成另一种形式,可能更会容易求解。下面就介绍一种常见的转换形式,对偶问题。
我们先来看一个与原问题等价的问题。设
θ(w)=maxα≥0,βL(w,α,β)注意条件,所有的αi≥0
注意所有的 αi
α
i
都是大于等于0的。
容易得出
θ(w)={f(w)所有等式和不等式约束均被满足+∞,有任意一个约束未被满足
如果不等式约束中有任意一个约束未被满足,比如若某个 w∗ w ∗ 使得 gi(w∗)>0 g i ( w ∗ ) > 0 时, 那我们将对应的 αi α i 取 +∞ + ∞ ,则 αigi(w∗) α i g i ( w ∗ ) 必然也是 +∞ + ∞ ,导致 θ(w∗) θ ( w ∗ ) 变为 +∞ + ∞ 。
同理如果原问题的等式约束中有任意一个约束未被满足,比如若某个w∗ w ∗ 使得 hj(w∗)≠0 h j ( w ∗ ) ≠ 0 时, 那我们将对应的βj β j 取βj={−∞hj(w∗)<0+∞,hj(w∗)>0β j = { − ∞ h j ( w ∗ ) < 0 + ∞ , h j ( w ∗ ) > 0
则 βjhj(w∗) β j h j ( w ∗ ) 必然是 +∞ + ∞ ,,导致 θ(w∗) θ ( w ∗ ) 变为 +∞ + ∞ 。
只有当 w∗ w ∗ 满足所有的等式约束和不等式约束时, θ(w∗) θ ( w ∗ ) 才不会变为无穷大。而且由于此时等式约束被满足,导致所有的 βjhj(w∗) β j h j ( w ∗ ) 项被直接消去,因为他们都等于0;另一方面由于所有的 αi≥0,gi(w∗)≤0 α i ≥ 0 , g i ( w ∗ ) ≤ 0 ,因此 αigi(w∗) α i g i ( w ∗ ) 取最大时必然也是0,即所有的 αigi(w∗) α i g i ( w ∗ ) 项也被消去,只剩下了 f(w) f ( w ) 。于是就有上面的结果
θ(w)={f(w)constraint satisfied+∞,constraint not satisfiedθ ( w ) = { f ( w ) constraint satisfied + ∞ , constraint not satisfied
这样一来,求原问题中的 minwf(w)
min
w
f
(
w
)
就等价于求 minwθ(w)
min
w
θ
(
w
)
。
原问题等价于:
objective:minwmaxα,βL(w,α,β)s.t.αi≥0,for i=1,2,3...n
如果调换上面 min 和 max 的顺序,就得到该问题的对偶问题。
对偶问题 :
objective:maxα,βminwL(w,α,β)s.t.αi≥0,for i=1,2,3...n
引入一个新函数: θD(α,β)=minwL(w,α,β) θ D ( α , β ) = min w L ( w , α , β ) ,这时对偶问题变成:
objective:maxα,βθD(α,β)s.t.αi≥0,for i=1,2,3...n
根据θD
θ
D
的定义可知,对于任意的(w,β,α≥0)
(
w
,
β
,
α
≥
0
)
,有θD(α,β)≤L(w,α,β)
θ
D
(
α
,
β
)
≤
L
(
w
,
α
,
β
)
;
根据θ
θ
的定义可知,对于任意的(w,β,α≥0)
(
w
,
β
,
α
≥
0
)
,有θ(w)≥L(w,α,β)
θ
(
w
)
≥
L
(
w
,
α
,
β
)
;
如果设p∗=θ(w∗)=minwθ(w),d∗=θD(α∗,β∗)=maxα≥0,βθD(α,β)
则 d∗=θD(α∗,β∗)≤L(w∗,α∗,β∗)≤θ(w∗)=p∗
即 d∗≤p∗ d ∗ ≤ p ∗ ,这个特性被称为”弱对偶性”, (p∗−d∗) ( p ∗ − d ∗ ) 被称为”对偶间隙”,对偶间隙是大于等于0的。通过求解对偶问题,可以求出原问题的一个下限,在实际中这对寻求原问题最优解有一定的帮助。
如果对偶间隙为0即 d∗=p∗ d ∗ = p ∗ ,则称之为”强对偶性”,此时对偶问题于原问题等价,只需求解对偶问题即可, (w∗,α∗,β∗) ( w ∗ , α ∗ , β ∗ ) 同时是原问题和对偶问题的解。
那什么情况下强对偶性才能被满足呢?我们介绍一个能在 凸优化问题中保证强对偶性的充分条件,下一节再证明这个结论。
定义: 凸优化问题
当且仅当目标函数f(w) f ( w ) 和所有的不等式约束函数gi(w) g i ( w ) 都是凸函数,所有的等式约束hj(w) h j ( w ) 都是线性(仿射)函数时,相应的最优化问题属于凸优化问题。
Slater条件
对于凸优化问题,如果可行域满足Slater条件,强对偶性保证成立。
Slater条件是指,可行域存在一点 w′ w ′ 同时满足:{gi(w′)<0for i=1,2...n (注意是<不再是≤)hj(w′)=0for j=1,2...m{ g i ( w ′ ) < 0 f o r i = 1 , 2... n ( 注 意 是 < 不 再 是 ≤ ) h j ( w ′ ) = 0 f o r j = 1 , 2... m
如果不等式约束中存在线性约束,比如前 t t 个不等式约束都是线性约束时,Slater条件可以弱化为:{gi(w′)≤0for i=1,2...tgi(w′)<0for i=t+1,t+2...nhj(w′)=0for j=1,2...m
KKT条件的充分性
之前的分析中,KKT条件只能作为最优解的必要条件,但满足KKT条件的解不一定是最优解。而对于凸优化问题,KKT条件同时也是最优解的充分条件。
如果(w∗,α∗,β∗) ( w ∗ , α ∗ , β ∗ ) 是满足KKT条件的一组解,即
{∂L∂w∗k=0for k=1,2,3...dw(w的维数)∂L∂β∗j=0for j=1,2...mα∗i⋅∂L∂α∗i=0for i=1,2...nα∗i≥0,∂L∂α∗i≤0for i=1,2...n{ ∂ L ∂ w k ∗ = 0 f o r k = 1 , 2 , 3... d w ( w 的 维 数 ) ∂ L ∂ β j ∗ = 0 f o r j = 1 , 2... m α i ∗ ⋅ ∂ L ∂ α i ∗ = 0 f o r i = 1 , 2... n α i ∗ ≥ 0 , ∂ L ∂ α i ∗ ≤ 0 f o r i = 1 , 2... n
由于 α∗≥0 α ∗ ≥ 0 ,以及凸优化问题中各不等式约束函数和目标函数都是凸函数的特点,易知 L(w,α∗,β∗) L ( w , α ∗ , β ∗ ) 是 w w 的凸函数,而KKT条件的第一行说明w∗是使得 L(w,α∗,β∗) L ( w , α ∗ , β ∗ ) 对 w w 导数为0的点,因此
L(w∗,α∗,β∗)=minwL(w,α∗,β∗)=θD(α∗,β∗)
同时,KKT条件的第二行 h(w∗)=0 h ( w ∗ ) = 0 和第三行 α∗g(w∗)=0 α ∗ g ( w ∗ ) = 0 使得
L(w∗,α∗,β∗)=f(w∗)=θ(w∗)L ( w ∗ , α ∗ , β ∗ ) = f ( w ∗ ) = θ ( w ∗ )
因此有 θD(α∗,β∗)=θ(w∗) θ D ( α ∗ , β ∗ ) = θ ( w ∗ ) 。
而同时 θD(α∗,β∗)≤d∗≤p∗≤θ(w∗) θ D ( α ∗ , β ∗ ) ≤ d ∗ ≤ p ∗ ≤ θ ( w ∗ ) ,这其实暗示了 d∗=p∗ d ∗ = p ∗ ,即强对偶性成立,且 (w∗,α∗,β∗) ( w ∗ , α ∗ , β ∗ ) 正好是原问题和对偶问题的最优解。
因此,对于凸优化问题,满足KKT条件的解一定是最优解,且满足KKT条件暗示了强对偶性成立。
4. 强对偶性的证明与Slater条件
强对偶性的一种比较直观的证明是用几何方法。
先介绍一条关于凸集的定理。这个定理表达的意思很直观。比如在二维空间中,二维平面上的任意一个凸图形(比如一个圆),在其边缘上任一点处做切线,该图形必在切线的同一侧,而不会被切割成多个部分并分居两侧。该定理的完整表述如下:
引理: 支撑超平面定理
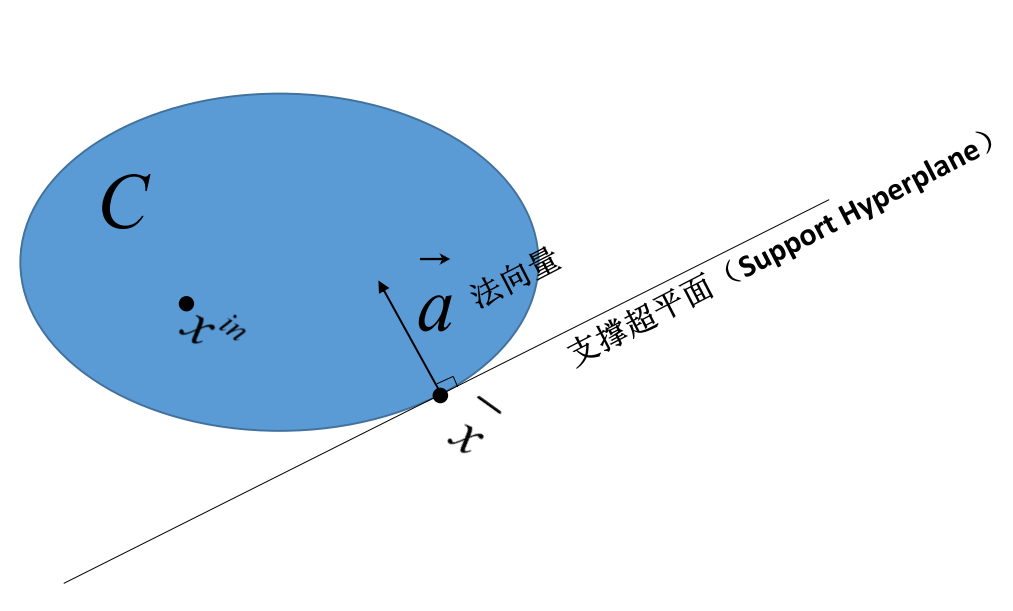
设集合 C C 是 Rn 空间中的闭凸集, ˉx x ¯ 是 C C 边界上一点,则必存在一个过点 ˉx 的超平面,使得 C C 位于它的一个闭半空间。即存在法向量 a ,使得对于 C C 中任意点 x ,有:
a⋅x−a⋅ˉx≥0a ⋅ x − a ⋅ x ¯ ≥ 0
进一步地,如果已知 xin x i n 是 C C 的一个内点,则:
a⋅xin−a⋅ˉx>0
如果想了解该定理的证明看这里:
http://www.cnblogs.com/murongxixi/p/3615034.html
这是在网上找到的一篇博文,里面步骤比较详尽。为防止原链接失效,相关的重要证明步骤会以图片形式插入到本文末尾的附录中。
回到我们的问题。我们要研究的是凸优化问题中强对偶性成立的条件,首先做一个基本假设:
基本假设:假设原问题是凸优化问题,即f(w),gi(w) f ( w ) , g i ( w ) 都是凸函数,hj(w) h j ( w ) 都是线性函数,且所有的hj(w) h j ( w ) 相互之间都是线性独立的。
w∈Rdw
w
∈
R
d
w
,我们按如下方式将Rdw
R
d
w
空间中一点w
w
映射为R(n+m+1)空间中的点E
E
:
E(w)=(u1,u2,...un,v1,v2,...vm,t)其中{ui=gi(w)i=1,2,3...nvj=hj(w)j=1,2,3...mt=f(w)
简化表示为E=(u,v,t) E = ( u , v , t ) 。
设所有点E
E
组成的集合为Go,
Go={(u,v,t):u=g(w),v=h(w),t=f(w),w∈Rdw}
G
o
=
{
(
u
,
v
,
t
)
:
u
=
g
(
w
)
,
v
=
h
(
w
)
,
t
=
f
(
w
)
,
w
∈
R
d
w
}
然而,即便有了前面的基本假设,我们也不能保证Go
G
o
是凸集。但是如果把它简单扩展一下,设:
Ge={(u,v,t):u≥g(w),v=h(w),t≥f(w),w∈Rdw}
容易证明Ge G e 是一个凸集,且Go⊆Ge G o ⊆ G e 。
若A(ua,va,ta) A ( u a , v a , t a ) 和B(ub,vb,tb) B ( u b , v b , t b ) 是Ge G e 内的两个点,按照Ge G e 的定义可知必然存在wa w a 和wb w b ,使得
va=h(wa),ua≥g(wa),ta≥f(wa)vb=h(wb),ub≥g(wb),tb≥f(wb)v a = h ( w a ) , u a ≥ g ( w a ) , t a ≥ f ( w a ) v b = h ( w b ) , u b ≥ g ( w b ) , t b ≥ f ( w b )
设 0≤c≤1,wc=cwa+(1−c)wb,C=cA+(1−c)B=(uc,vc,tc) 0 ≤ c ≤ 1 , w c = c w a + ( 1 − c ) w b , C = c A + ( 1 − c ) B = ( u c , v c , t c ) ,则
uc=cua+(1−c)ubvc=cva+(1−c)vbtc=cta+(1−c)tbu c = c u a + ( 1 − c ) u b v c = c v a + ( 1 − c ) v b t c = c t a + ( 1 − c ) t b
由于 h(w) h ( w ) 是 w w 的线性函数,因此
c⋅h(wa)+(1−c)h(wb)=h[cwa+(1−c)wb]=h(wc)
即 vc=h(wc) v c = h ( w c ) ;
由于 g(w),f(w) g ( w ) , f ( w ) 都是 w w 的凸函数,因此
c⋅g(wa)+(1−c)g(wb)≥g[cwa+(1−c)wb]=g(wc)c⋅f(wa)+(1−c)f(wb)≥f[cwa+(1−c)wb]=f(wc)
而同时 ua≥g(wa),ta≥f(wa),ub≥g(wb),tb≥f(wb) u a ≥ g ( w a ) , t a ≥ f ( w a ) , u b ≥ g ( w b ) , t b ≥ f ( w b ) ,于是
cua+(1−c)ub≥c⋅g(wa)+(1−c)g(wb)cta+(1−c)tb≥c⋅f(wa)+(1−c)f(wb)c u a + ( 1 − c ) u b ≥ c ⋅ g ( w a ) + ( 1 − c ) g ( w b ) c t a + ( 1 − c ) t b ≥ c ⋅ f ( w a ) + ( 1 − c ) f ( w b )
即 uc≥g(wc),tc≥f(wc) u c ≥ g ( w c ) , t c ≥ f ( w c ) 。再结合 vc=h(wc) v c = h ( w c ) ,可知 (uc,vc,tc)∈Ge ( u c , v c , t c ) ∈ G e ,即 C=cA+(1−c)B∈Ge C = c A + ( 1 − c ) B ∈ G e 。由于前述 A,B,c A , B , c 的选取具有任意性,因此对于任意两点 A,B∈Ge A , B ∈ G e ,连线 ¯AB A B ¯ 上的所有点都属于 Ge G e , Ge G e 是凸集。
除此之外,我们还知道E∗=(0,0,p∗) E ∗ = ( 0 , 0 , p ∗ ) 必是Ge G e 的一个边界点,其中p∗=minwθ(w) p ∗ = min w θ ( w ) ,θ(w) θ ( w ) 的定义同上一节。
若w∗ w ∗ 是目标函数f(w) f ( w ) 在可行域内的极小点,则p∗=f(w∗) p ∗ = f ( w ∗ ) ,且由于在可行域内,必然满足g(w∗)≤0 g ( w ∗ ) ≤ 0 、h(w∗)=0 h ( w ∗ ) = 0 ,因此(0,0,p∗)∈Ge ( 0 , 0 , p ∗ ) ∈ G e ;
又由于p∗ p ∗ 是可行域上即区间 {g(w∗)≤0,h(w∗)=0} { g ( w ∗ ) ≤ 0 , h ( w ∗ ) = 0 } 上的最小值(边界值),对于任意小的正数δ δ ,(0,0,p∗−δ)∉Ge ( 0 , 0 , p ∗ − δ ) ∉ G e ,因此(0,0,p∗) ( 0 , 0 , p ∗ ) 在边界上。
即E∗=(0,0,p∗) E ∗ = ( 0 , 0 , p ∗ ) 是Ge G e 的一个边界点。
利用上面关于边界点的支撑超平面定理,我们知道必存在一个法向量a=(αa,βa,γa)
a
=
(
α
a
,
β
a
,
γ
a
)
,使得对于Ge
G
e
内任一点Ee=(ue,ve,te)
E
e
=
(
u
e
,
v
e
,
t
e
)
,满足:
a⋅Ee−a⋅E∗≥0即αaue+βave+γate≥γap∗
由于 ue,te u e , t e 可以随意取正无穷大, p∗ p ∗ 是个定值,为使上面的大于等于恒成立, αa α a 和 γa γ a 必须大于等于0。否则,如果他们任意一个取负,当 ue,te u e , t e 取正无穷大时,左边会变成负无穷而导致上式无法被满足。
h(w) h ( w ) 是w w 的线性函数,因此ve=h(w)也可以取到正无穷,甚至负无穷也可以。但ve v e 不能单独、随意 地增大,因为ve v e 完全由w w 确定,而ue和te只是被w w 确定了下限,它们可以单独增大,且仍保证在集合Ge内。
γa>0 γ a > 0 的情况
假如γa≠0
γ
a
≠
0
,此时令α∗=αa/γa,β∗=βa/γa
α
∗
=
α
a
/
γ
a
,
β
∗
=
β
a
/
γ
a
,则式(1-a)可重写如下:
α∗ue+β∗ve+te≥p∗
由于 αa≥0 α a ≥ 0 , α∗≥0 α ∗ ≥ 0 。
由于 Go⊆Ge G o ⊆ G e ,因此 Go G o 中任意一点 E(u,v,t)=(g(w),h(w),f(w)) E ( u , v , t ) = ( g ( w ) , h ( w ) , f ( w ) ) 也都满足上式。
即必然存在一组 α∗,β∗ α ∗ , β ∗ ,对任意的 w∈Rdw w ∈ R d w ,始终满足:
α∗g(w)+β∗h(w)+f(w)≥p∗α≥0
我们上面都使用了简化后的表示方式,如果将上式完整展开,就是:存在一组 α∗,β∗ α ∗ , β ∗ 使得下式对所有的 w∈Rdw w ∈ R d w 成立。
n∑i=1α∗igi(w)+m∑j=1β∗jhj(w)+f(w)=L(w,α∗,β∗)≥p∗α∗i≥0,for i=1,2,3...n
由于上式对任意的w
w
都成立,因此
θD(α∗,β∗)=minwL(w,α∗,β∗)≥p∗
进一步由于d∗=maxα≥0,βθD(α,β)≥θD(α∗,β∗)
于是得到 d∗≥p∗ d ∗ ≥ p ∗ 。而由弱对偶性, d∗≤p∗ d ∗ ≤ p ∗ 。因此 d∗=p∗ d ∗ = p ∗ ,强对偶性成立。
γa=0 γ a = 0 的情况,Slater条件的作用
这不是我们期望出现的情况,因为一旦γa=0 γ a = 0 ,我们就无法将式(1-a)的左边转换成跟L(w,α,β) L ( w , α , β ) 相同的形式了。实际上,只要上节中提到的Slater条件被满足(通常这个条件都是满足的),就不会出现γa=0 γ a = 0 的情况。下面我们分析为什么不会出现。
假如γa=0
γ
a
=
0
,此时式(1-a)变成
αaue+βave+γate≥0
Slater条件保证了在可行域内,存在 w′
w
′
使得g(w′)<0,h(w′)=0
g
(
w
′
)
<
0
,
h
(
w
′
)
=
0
,设
E1=(g(w′),h(w′),f(w′))∈GeE2=(g(w′)+Δg,h(w′),f(w′)+Δf)∈int Ge其中Δg和Δf是任意大于0的值,这两个正增量保证了E2是Ge的内点
则有
αag(w′)+βah(w′)+γaf(w′)≥0
αa[g(w′)+Δg]+βah(w′)+γa[f(w′)+Δf]>0
式(4-c)中可以用大于号是因为 E2是Ge的内点 E 2 是 G e 的 内 点 ,上面介绍引理时专门提到对于内点可以用大于号。
考虑到 h(w′)=0,γa=0 h ( w ′ ) = 0 , γ a = 0 ,由式(4-b)可得 αag(w′)≥0 α a g ( w ′ ) ≥ 0 ;
再由 g(w′)<0,α≥0 g ( w ′ ) < 0 , α ≥ 0 ,可得 αa=0 α a = 0 ;
而将 αa=0 α a = 0 和 h(w′)=0,γa=0 h ( w ′ ) = 0 , γ a = 0 代入式(4-c),会得到式(4-c)左边等于0的结论,这与式(4-c)中的大于号矛盾。
因此, 当Slater条件被满足时,不会出现γa=0 γ a = 0 的情况。
Slater条件的表述似乎加强了对可行域的要求。实际上,只要要求对于每一个不等式约束 gi(w) g i ( w ) ,在可行域内分别存在一个 wi w i 能使得gi(wi)<0 g i ( w i ) < 0 即可,这就足以支持我们推出上面的矛盾(将上面的简化表达式完整展开并推导出每个αi=0 α i = 0 即可推出矛盾)。而不须要求存在某个 w′ w ′ 使其同时满足所有的不等式约束。然而如果所有的gi(w) g i ( w ) 都是连续可导的话,这两种表述似乎也是等价的,不过这个结论的推理过程可能有些繁杂。
之前还提到了弱化的Slater条件(Weak Slater Condition),弱化的Slater条件放宽了对线性不等式约束的要求。
实际上,当原Slater条件未被满足,但弱化的Slater条件能被满足时,说明存在某个线性不等式约束 gi(w) g i ( w ) ,在可行域内找不到任何点能使得gi(w)<0 g i ( w ) < 0 成立,即在整个可行域内gi(w)=0 g i ( w ) = 0 。这意味着所有等式约束hj(w)=0 h j ( w ) = 0 ,它们与gi(w)≤0 g i ( w ) ≤ 0 的交集和与gi(w)=0 g i ( w ) = 0 的交集一样。考虑到hj(w) h j ( w ) 和gi(w) g i ( w ) 都是w w 的线性函数,这只会发生在gi(w)正好是所有所有等式约束hj(w) h j ( w ) 的线性组合时,即
gi(w)=m∑j=1cjhj(w)g i ( w ) = ∑ j = 1 m c j h j ( w )
而这时,可以认为g_i(w)完全不起约束作用,直接为其分配系数 αi=0 α i = 0 ,然后按正常方式为其他不等式约束分配系数即可。因此只要满足弱化的Slater条件,就可以保证强对偶性。
结论
综上,只要f(w),gi(w)都是凸函数,hj(w)都是线性函数,且可行域满足弱化的Slater条件时,强对偶性可以被保证。
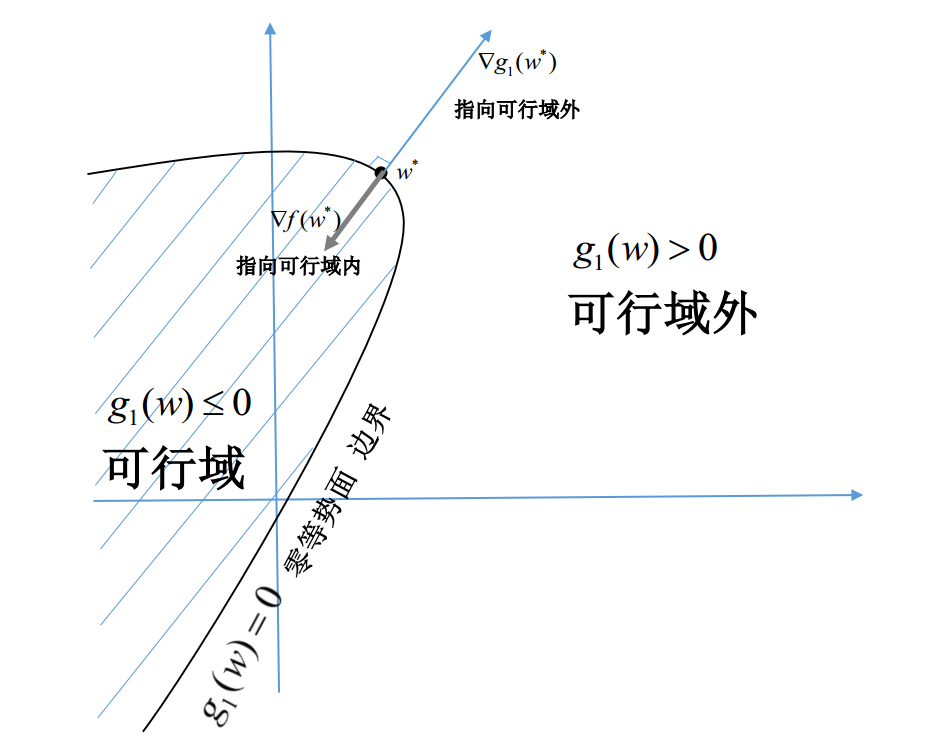
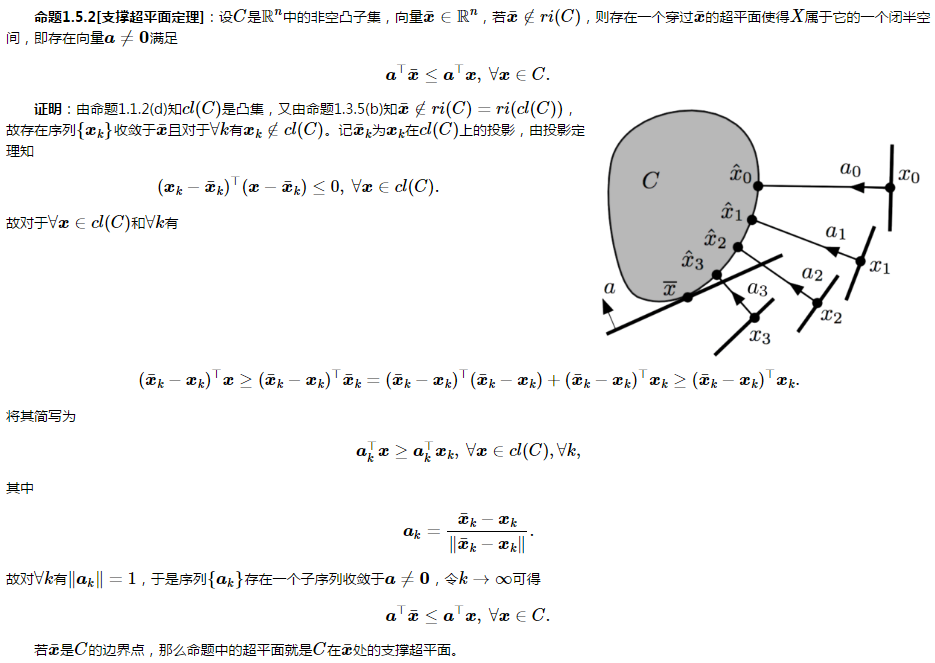
附录:支撑超平面定理的证明(截图)
以下截图来自博文:
http://www.cnblogs.com/murongxixi/p/3615034.html


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








