3D数学 学习笔记（3） 欧拉角与四元数

3D数学 学习笔记（3） 欧拉角与四元数

参考书籍：
《3D数学基础：图形与游戏开发》
【Numberphile数字狂】神奇四元数

---

常用矩阵和四元数表示“角位移”，用欧拉角表示“方位”。

欧拉角

常用约定“heading-pitch-bank”

围绕轴分别代表：y、x、z，使用的是左手坐标系，从惯性坐标系到物体坐标系。要注意的是**heading使用的是惯性坐标，pitch和bank使用的是物体坐标系。这也是形成万向锁的原因（heading为惯性坐标）。**在Unity中，面板中Transform的Rotation就是使用这个约定。通常规定heading和bank范围在[-180°,180°]，pitch范围在[-90°,90°]。

“roll-pitch-yaw”

围绕轴分别代表：z、x、y，从物体坐标系到惯性坐标系。不同于上面那个y，这个yaw代表的是物体坐标系。

heading 和 yaw的区别：

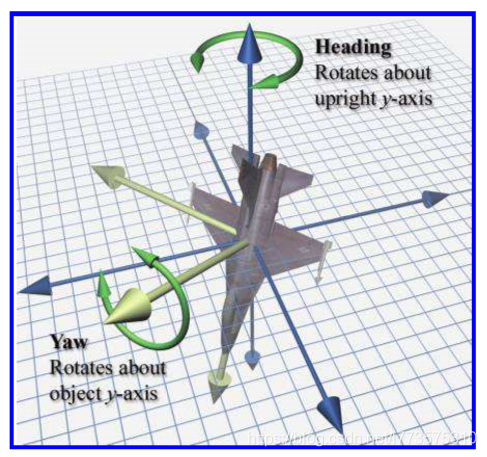
万向锁

如果pitch角为±90°，则第一次（y轴）和第三次（z轴）旋转轴相同。y是惯性坐标，一直向上，pitch转到±90°，bank轴就会和竖直轴平行。为了消除这种两个轴同时控制同一个方向的现象，规定在万向锁情况下，只使用heading来控制竖直轴，及pitch为±90°时，bank为0。

插值计算

wrap(x)：将x限制在(-180°,180°]，下面公式中’⌊⌋'符号表示：符号内的值向下取整。

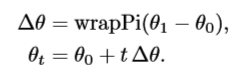
在Unity中，实现wrapPi(x)也可以直接调用Mathf.Repeat()实现。伪代码如下：
wrapPi(x) = Mathf.Repeat(x,360°) - 180°

---

四元数

绕n轴旋转θ角。

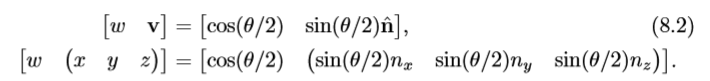
负四元数

q和-q代表的实际角位移是相同的。因为-q旋转轴倒置，同时转相反方向，就像正面的顺时针和反面的逆时针其实是一个结果。

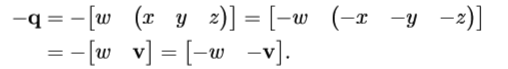
单位四元数（Identity）

• [1, 0]
  [-1, 0]虽然代表相同角位移，但是在数学上是不相同。

四元数的模

如果为了用四元数表示方位，就要符合这个规则的单位四元数。

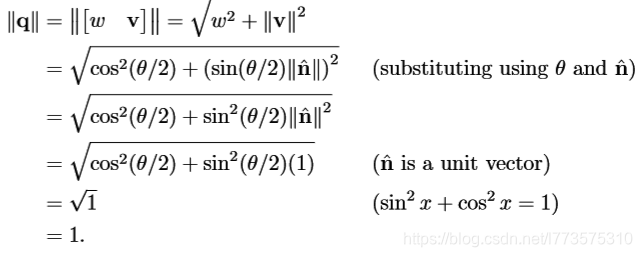
四元数共轭

即轴反向。

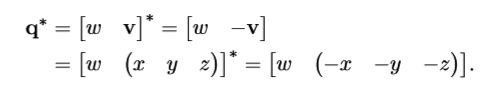
四元数的逆

q乘以q^-1可以得到单位四元数[1, 0]。

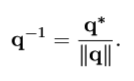
四元数乘法（叉乘）

四元数乘法实际就是旋转。

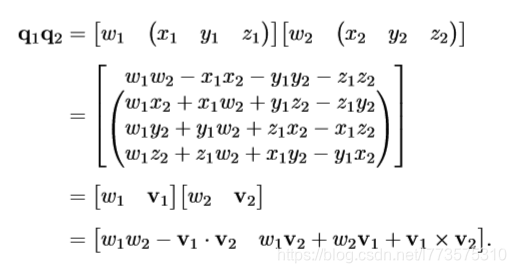
• (ab)c = a(bc)
• ab ≠ ba
• ‖q₁q₂‖ = ‖q₁‖‖q₂‖
• (ab)^-1 = b^-1a^-1 （可扩展到多个四元数）

实现点p绕n旋转，q为[cos(θ/2), sin(θ/2)]：
p’ = qpq^-1

先绕a旋转，后绕b旋转。要注意的是执行计算顺序是倒过来的：

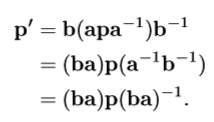
四元数的“差”（角位移）

一个方位（a）到另一个方位（b）的角位移（d），即da = b。执行顺序从右往左。

推导过程，两边同时右乘a^-1：

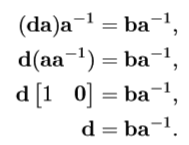
四元数的点乘

类似与向量点乘，a·b越大，a和b代表的角位移就越相似。对于单位四元数a和b，有 -1 ≤ a·b ≤ 1。

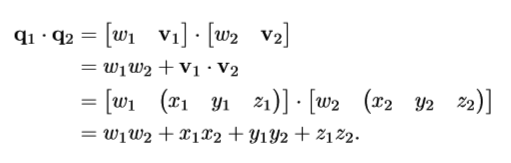
四元数的对数

结果一般不是单位四元数。

四元数的指数

结果总是单位四元数。

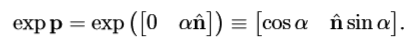
四元数求幂

可以理解为角度缩放。当t从0到1时，四元数q从[1, 0]变到q。q^1/3表示q的三分之一个角位移，即如果q表示绕x轴绕90度，q^1/3就表示绕x轴绕30度。不过一般的指数运算对四元数都不适用，如(q⁴)^1/2 ≠ q²，(q^s)^t ≠ q^st。

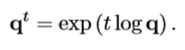
四元数插值slerp（Spherical Linear Interpolation）

理论上计算过程：

1. 计算四元数的差：∆q = q₁q₀^-1
2. 计算差的一部分（求幂）：(∆q)^t
3. 最后从开始值加上这个部分（叉乘）：(∆q)^tq₀

实际用更有效的方法：
即理解为两个向量之间求弧插值。投影到一个2D平面，即可方便推导出结果。角度w可以用点乘来算。

需要注意的是：

• 因为q和-q虽然代表相同方位，但是计算的时候结果会不一样。解决方案是点乘结果如果为负就反转。
• 如果q₀和q₁非常接近（点乘接近1，sinθ非常小），除法可能会有问题。解决方案是直接用线性插值计算。

---

矩阵、欧拉角和四元数比较

• 坐标间转换向量，选择矩阵形式。
• 需要大量保存方位数据（如动画）时，使用欧拉角或四元数。嵌套坐标系之间的连接，用四元数。
• 平滑插值只能用四元数。

---

表达形式之间的转换

欧拉角转换到矩阵

HPB（heading pitch bank），可参考最上面欧拉角。
物体坐标到惯性坐标

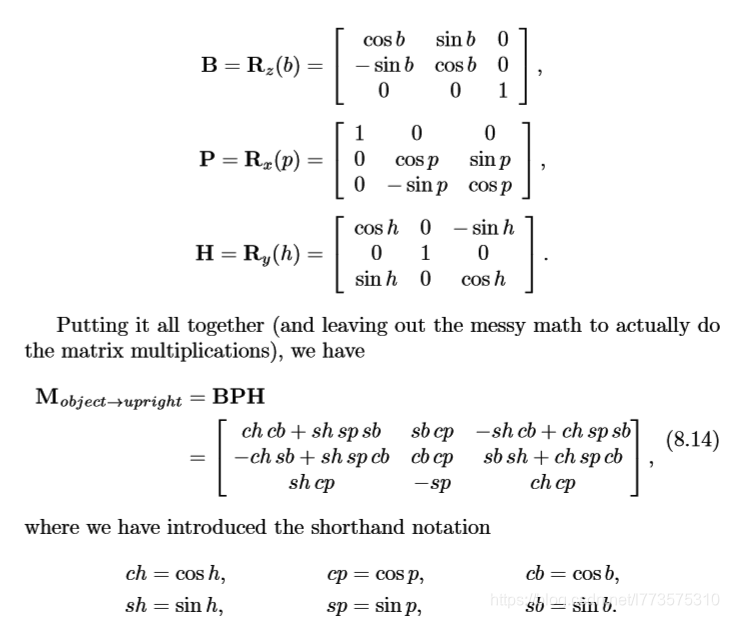
惯性坐标到物体坐标

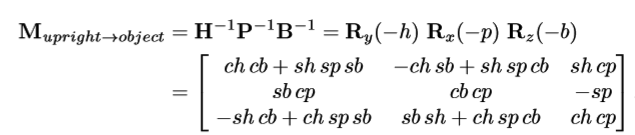
矩阵转换到欧拉角

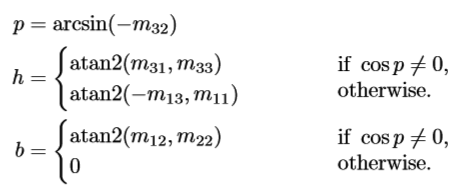
直接通过三角函数计算即可，不过注意一些特殊角度如90°等，需要判断和赋特殊值。
下面是物体到惯性坐标下hpb的计算（部分过程省略）：

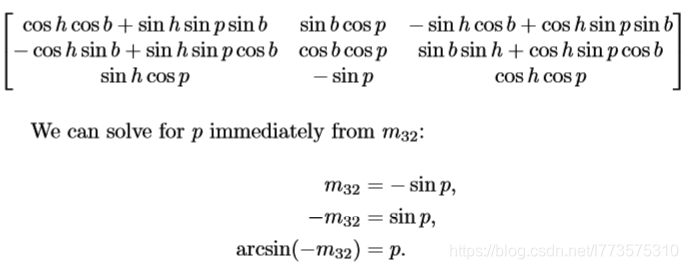
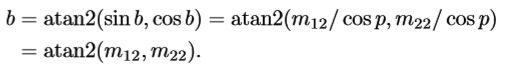
在cosp = 0时，p = ±90°，即面向上或向下，万向锁，设置b为0。p和h的值可以直接算出来了。

四元数转到矩阵

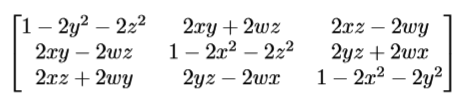
矩阵转到四元数

下图方法计算都为正值，没有选择正根还是负根的依据。

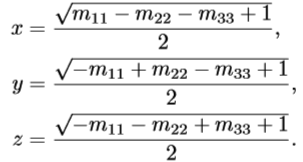
但是可以用任意一个非负根来计算另外三个分量的值。

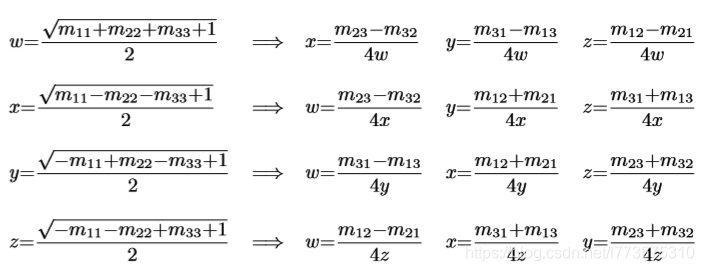
建议先判断w,x,y,z中最大一个，用矩阵的对角线来计算该元素，然后用上图计算其他三个。

欧拉角转四元数

物体-惯性四元数 是 惯性-物体四元数的共轭。

四元数转欧拉角

先从四元数转矩阵，再从矩阵转到欧拉角。

---

在Unity中的应用

对Vector3向量方向旋转方法：四元数 * 3D方向向量。（注意顺序）

Quaternion rotation;	//旋转角度
Vector3 direction;		//原始方向

newDirection = rotation * direction;	//旋转后的方向

子物体旋转角转换到世界坐标下的旋转角：父对象旋转角 * 子对象旋转角。

newRotation = transfrom.rotation * subRotation;