http://blog.csdn.net/pipisorry/article/details/49516209
高斯分布(正态分布)
若随机变量X服从一个数学期望为μ、方差为σ^2的高斯分布,记为N(μ,σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。
正态随机变量概率密度函数φ(x)
正态分布曲线性质
2.正态曲线关于直线x=μ对称。
3.σ越大,正态曲线越扁平;σ越小,正态曲线越尖陡。
4.在正态曲线下方和x轴上方范围内区域面积为1。
5. 3σ原则:P(μ-σ<X≤μ+σ)=68.3%P(μ-2σ<X≤μ+2σ)=95.4%P(μ-3σ<X≤μ+3σ)=99.7%
6.如果
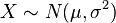 且a与b是
实数,那么aX + b∼N(aμ + b,(aσ)2) (参见
期望值和
方差).
且a与b是
实数,那么aX + b∼N(aμ + b,(aσ)2) (参见
期望值和
方差).
7.如果
 与
与
 是
统计独立的正态
随机变量,那么:
是
统计独立的正态
随机变量,那么:
它们的和也满足正态分布
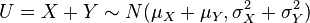 (
proof).
(
proof).
它们的差也满足正态分布
 .
.
U与V两者是相互独立的。
8.如果
 和
和
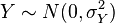 是独立正态随机变量,那么:
是独立正态随机变量,那么:
它们的积XY服从概率密度函数为p的分布
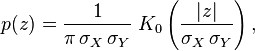 其中K0是贝塞尔函数(modified Bessel function)
其中K0是贝塞尔函数(modified Bessel function)- 它们的比符合柯西分布,满足X / Y∼Cauchy(0,σX / σY).
 为独立标准正态随机变量,那么
为独立标准正态随机变量,那么
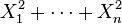 服从自由度为n的
卡方分布。
服从自由度为n的
卡方分布。
一般正态分布N(μ,σ^2)转换成标准正态分布N(0, 1)
正态分布归一化的证明
正态(高斯)分布于统计学,就如水养育生命一样重要,而掌握正态分布的一些性质及其相关证明,也是一项基本功。接下来,我们证明正态分布密度函数的归一化,这是PRML讲解正态分布时的第一个练习题,我们的证明参考了这个习题的答案,其中采用的积分方法非常巧妙。
问题的描述如下:如果随机变量 X 满足均值为 μ ,方差为 σ2 的正态分布,那么其密度函数为:
我们要证明的是:
问题的关键在于求解如下积分:
为了求解 I ,可以先求 I2 ,而 I2 可以写成二重积分的形式:
将上述二重积分转换为极坐标形式:
I2 可以写成:
其中:
因此:
利用分部积分法求 I2 :
从而证明了均值为0的正态分布密度函数的归一化:
利用积分的换元法:
因此证明了 N(x∣μ,σ2) 的归一化:
累积分布函数Φ(x)
累积分布函数是指随机变量X小于或等于x的概率,用密度函数表示为
正态分布的累积分布函数能够由一个叫做误差函数的特殊函数表示:
标准正态分布的累积分布函数习惯上记为Φ,它仅仅是指μ = 0,σ = 1时的值,
将一般正态分布用误差函数表示的公式简化,可得:
它的反函数被称为反误差函数,为:
该分位数函数有时也被称为probit函数。probit函数已被证明没有初等原函数。
正态分布的分布函数Φ(x)没有解析表达式,它的值可以通过数值积分、泰勒级数或者渐进序列近似得到。
概率密度函数的累积分布函数

单变量高斯分布
多维高斯分布

where μis the mean, Σthe covariance matrix, and k is the dimension of the space where x takes values.
其中
从多元高斯分布中抽取的样本大部分落在由 μ 和 Σ 所确定的一个区域里,该区域的中心由向量 μ 决定,区域大小由协方差矩阵 Σ 决定。
从式子(2.1)可以看出,当指数项为常数时,密度 p(x) 值不变,因此等密度点是使指数项为常数的点,即满足:
上式的解是一个超椭圆面,且其主轴方向由
∑
的特征向量所决定,主轴的长度与相应的协方差矩阵
Σ
的特征值成正比。
在数理统计中,式子(2.7)所表示的数量:
称为 x 到 μ 的Mahalanobis距离的平方。所以等密度点轨迹是 x 到 μ 的Mahalanobis距离为常数的超椭球面。
这个超椭球体大小是样本对于均值向量的离散度度量。对应的M式距离为 γ 的超椭球体积为:
如果多元高斯随机向量 x 的协方差矩阵是对角矩阵,则 x 的分量是相互独立的高斯分布随机变量。
[高斯分布-笔记(1) ] [PRML]
σ大小对features的影响
Note: if σ^2 is large,value of the feature falls away much more slowly. the width of this bell-shaped curve,σ is also called standard deviation.
[Ng ml course]
高维高斯分布的概率质量行为研究
如果我们从笛卡尔坐标系变换到极坐标系,然后把方向变量积分出来,我们就得到了一个概率密度的表达式 p(r) ,这个表达式是关于距离原点的半径 r 的函数。因此 p(r)δr 就是位于半径 r 处厚度为 δr 的薄球壳内部的概率质量。对于不同的 D 值,这个概率分布的图像如图所示。我们看到,对于大的 D 值,高斯分布的概率质量集中在薄球壳处。
不同的维度 D 中的高斯分布的概率密度关于半径 r 的关系。在高维空间中,高斯分布的大部分概率质量位于某个半径上的一个薄球壳上。
[PRML]
截断正态分布truncated normal distribution
(正对数分布又叫做截断正态分布)
π ( x ) ∝ N ( 1,1 ) I ( 0 ≤ x ≤ 4 )
截断高斯分布的概率密度函数pdf
其概率密度函数pdf要除以截断面积和sigma,使其pdf和为1。
There is an understanding that if b = ∞ {\displaystyle b=\infty }



截断正态分布数据生成
先生成相同mu, sigma的正态分布数据,取(a, b)之间的就可以了。(因为截断正态分布只是在截断区有数据,其概率相对大小没变)
截断正态分布的python分析
[截断正态分布(truncated normal distribution)]
[Truncated normal distribution]
[截断正态分布]
对数高斯分布
高斯分布的共轭分布
[主题模型TopicModel:LDA中的数学模型:高斯分布的共轭分布 ]
python中正态分布相关操作的实现
生成正态分布随机变量
在计算机模拟中,经常需要生成正态分布的数值。最基本的一个方法是使用标准的正态累积分布函数的反函数。除此之外还有其他更加高效的方法,Box-Muller变换就是其中之一。另一个更加快捷的方法是ziggurat算法。下面将介绍这两种方法。一个简单可行的并且容易编程的方法是:求12个在(0,1)上均匀分布的和,然后减6(12的一半)。这种方法可以用在很多应用中。这12个数的和是Irwin-Hall分布;选择一个方差12。这个随即推导的结果限制在(-6,6)之间,并且密度为12,是用11次多项式估计正态分布。
Box-Muller方法是以两组独立的随机数U和V,这两组数在(0,1]上均匀分布,用U和V生成两组独立的标准正态分布随即变量X和Y:
-
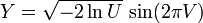 。
。
这个方程的提出是因为二自由度的卡方分布(见性质4)很容易由指数随机变量(方程中的lnU)生成。因而通过随机变量V可以选择一个均匀环绕圆圈的角度,用指数分布选择半径然后变换成(正态分布的)x,y坐标。
[统计函数库scipy.stats:连续分布-Norm高斯分布]
Box-Muller变换生成高斯分布数据的c++代码
#include<iostream>
using namespace std;
double generateGaussianNoise(double mu, double sigma){
const double epsilon = std::numeric_limits<double>::min();
const double two_pi = 2.0*3.14159265358979323846;
static double z0, z1;
static bool generate;
generate = !generate;
if (!generate)
return z1 * sigma + mu;
double u1, u2;
do {
u1 = rand() * (1.0 / RAND_MAX);
u2 = rand() * (1.0 / RAND_MAX);
} while (u1 <= epsilon);
z0 = sqrt(-2.0 * log(u1)) * cos(two_pi * u2);
z1 = sqrt(-2.0 * log(u1)) * sin(two_pi * u2);
return z0 * sigma + mu;
}
double getGaussian(double sigma_2, double* y, int T){
double mu = 0;
for (int i = 0; i < T; i++)
mu += y[i];
mu = mu / T;
return generateGaussianNoise(mu, sqrt(sigma_2 / T));
}
int __main(){
int N = 10;
double y[10] = { 5.0, 5.0, 5.0, 5.0, 5.0, 5.0, 5.0, 5.0, 5.0, 5.0 };
for (int i = 0; i < 10; i++)
cout << getGaussian(1.0, y, N) << endl;
return 0;
}
[Box-Muller transform.https://en.wikipedia.org/wiki/Box-Muller_transform]
绘制一维正态分布概率密度图
from scipy import stats import matplotlib.pyplot as plt x = np.linspace(stats.norm.ppf(0.01), stats.norm.ppf(0.99), 100) plt.plot(x, stats.norm.pdf(x), 'r-', alpha=0.6, label='norm pdf') plt.show()

绘制2维高斯分布图
import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() ax = Axes3D(fig) rv = stats.multivariate_normal([0, 0], cov=1) x, y = np.mgrid[-3:3:.15, -3:3:.15] ax.plot_surface(x, y, rv.pdf(np.dstack((x, y))), rstride=1, cstride=1) ax.set_zlim(0, 0.2) # savefig('../figures/plot3d_ex.png',dpi=48) plt.show()
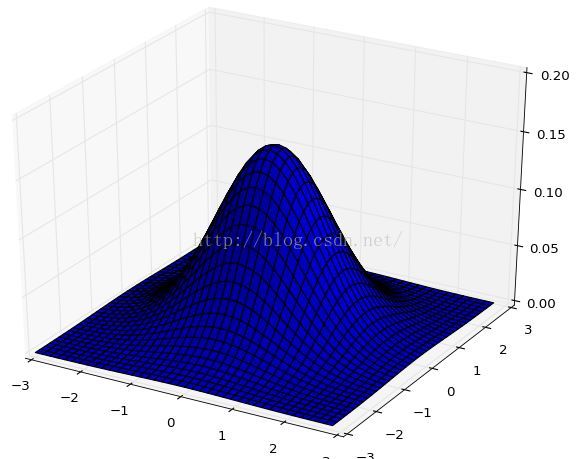
多维情况下固定一维绘制一维高斯分布
import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() ax = Axes3D(fig) rv = stats.multivariate_normal([0, 0], cov=1) x, y = np.meshgrid(np.linspace(0, 0, 400), np.linspace(-3, 3, 400)) ax.plot_surface(x, y, rv.pdf(np.dstack((x, y))), rstride=1, cstride=1) ax.set_zlim(0, 0.2) # savefig('../figures/plot3d_ex.png',dpi=48) plt.show()或者:
x, y = np.mgrid[-3:3:.15, -3:3:.15] x = np.zeros_like(x)
标准正态分布函数表
查表:lz只知道列为0时的查表,不懂列是啥意思(知道的希望留个言),从表中看出,cdf(x=0) = 0.5 [列0,行0],cdf(x=1) = 0.8413 [列值0,行值1], cdf(x=3) = 0.9987 [列值0,行值3]
示例:如计算Φ(3)-Φ(-1), 可知Φ(3)-Φ(-1) = Φ(3)-(1 - Φ(1)) = Φ(3) + Φ(1) - 1 = 0.84
| 标准正态分布函数表(形式1:sum=1) | ||||||||||
| φ(x) x | 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| x | ||||||||||
| 0 | 0.5 | 0.504 | 0.508 | 0.512 | 0.516 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
| 0.2 | 0.5793 | 0.5832 | 0.5871 | 0.591 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
| 0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6406 | 0.6443 | 0.648 | 0.6517 |
| 0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.67 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
| 0.5 | 0.6915 | 0.695 | 0.6985 | 0.7019 | 0.7054 | 0.7088 | 0.7123 | 0.7157 | 0.719 | 0.7224 |
| 0.6 | 0.7257 | 0.7291 | 0.7324 | 0.7357 | 0.7389 | 0.7422 | 0.7454 | 0.7486 | 0.7517 | 0.7549 |
| 0.7 | 0.758 | 0.7611 | 0.7642 | 0.7673 | 0.7703 | 0.7734 | 0.7764 | 0.7794 | 0.7823 | 0.7852 |
| 0.8 | 0.7881 | 0.791 | 0.7939 | 0.7967 | 0.7995 | 0.8023 | 0.8051 | 0.8078 | 0.8106 | 0.8133 |
| 0.9 | 0.8159 | 0.8186 | 0.8212 | 0.8238 | 0.8264 | 0.8289 | 0.8315 | 0.834 | 0.8365 | 0.8389 |
| 1 | 0.8413 | 0.8438 | 0.8461 | 0.8485 | 0.8508 | 0.8531 | 0.8554 | 0.8577 | 0.8599 | 0.8621 |
| 1.1 | 0.8643 | 0.8665 | 0.8686 | 0.8708 | 0.8729 | 0.8749 | 0.877 | 0.879 | 0.881 | 0.883 |
| 1.2 | 0.8849 | 0.8869 | 0.8888 | 0.8907 | 0.8925 | 0.8944 | 0.8962 | 0.898 | 0.8997 | 0.9015 |
| 1.3 | 0.9032 | 0.9049 | 0.9066 | 0.9082 | 0.9099 | 0.9115 | 0.9131 | 0.9147 | 0.9162 | 0.9177 |
| 1.4 | 0.9192 | 0.9207 | 0.9222 | 0.9236 | 0.9251 | 0.9265 | 0.9278 | 0.9292 | 0.9306 | 0.9319 |
| 1.5 | 0.9332 | 0.9345 | 0.9357 | 0.937 | 0.9382 | 0.9394 | 0.9406 | 0.9418 | 0.943 | 0.9441 |
| 1.6 | 0.9452 | 0.9463 | 0.9474 | 0.9484 | 0.9495 | 0.9505 | 0.9515 | 0.9525 | 0.9535 | 0.9545 |
| 1.7 | 0.9554 | 0.9564 | 0.9573 | 0.9582 | 0.9591 | 0.9599 | 0.9608 | 0.9616 | 0.9625 | 0.9633 |
| 1.8 | 0.9641 | 0.9648 | 0.9656 | 0.9664 | 0.9671 | 0.9678 | 0.9686 | 0.9693 | 0.97 | 0.9706 |
| 1.9 | 0.9713 | 0.9719 | 0.9726 | 0.9732 | 0.9738 | 0.9744 | 0.975 | 0.9756 | 0.9762 | 0.9767 |
| 2 | 0.9772 | 0.9778 | 0.9783 | 0.9788 | 0.9793 | 0.9798 | 0.9803 | 0.9808 | 0.9812 | 0.9817 |
| 2.1 | 0.9821 | 0.9826 | 0.983 | 0.9834 | 0.9838 | 0.9842 | 0.9846 | 0.985 | 0.9854 | 0.9857 |
| 2.2 | 0.9861 | 0.9864 | 0.9868 | 0.9871 | 0.9874 | 0.9878 | 0.9881 | 0.9884 | 0.9887 | 0.989 |
| 2.3 | 0.9893 | 0.9896 | 0.9898 | 0.9901 | 0.9904 | 0.9906 | 0.9909 | 0.9911 | 0.9913 | 0.9916 |
| 2.4 | 0.9918 | 0.992 | 0.9922 | 0.9925 | 0.9927 | 0.9929 | 0.9931 | 0.9932 | 0.9934 | 0.9936 |
| 2.5 | 0.9938 | 0.994 | 0.9941 | 0.9943 | 0.9945 | 0.9946 | 0.9948 | 0.9949 | 0.9951 | 0.9952 |
| 2.6 | 0.9953 | 0.9955 | 0.9956 | 0.9957 | 0.9959 | 0.996 | 0.9961 | 0.9962 | 0.9963 | 0.9964 |
| 2.7 | 0.9965 | 0.9966 | 0.9967 | 0.9968 | 0.9969 | 0.997 | 0.9971 | 0.9972 | 0.9973 | 0.9974 |
| 2.8 | 0.9974 | 0.9975 | 0.9976 | 0.9977 | 0.9977 | 0.9978 | 0.9979 | 0.9979 | 0.998 | 0.9981 |
| 2.9 | 0.9981 | 0.9982 | 0.9982 | 0.9983 | 0.9984 | 0.9984 | 0.9985 | 0.9985 | 0.9986 | 0.9986 |
| 3 | 0.9987 | 0.999 | 0.9993 | 0.9995 | 0.9997 | 0.9998 | 0.9998 | 0.9999 | 0.9999 | 1 |
| 3.1 | 0.999032 | 0.999065 | 0.999096 | 0.999126 | 0.999155 | 0.999184 | 0.999211 | 0.999238 | 0.999264 | 0.999289 |
| 3.2 | 0.999313 | 0.999336 | 0.999359 | 0.999381 | 0.999402 | 0.999423 | 0.999443 | 0.999462 | 0.999481 | 0.999499 |
| 3.3 | 0.999517 | 0.999534 | 0.999550 | 0.999566 | 0.999581 | 0.999596 | 0.999610 | 0.999624 | 0.999638 | 0.999660 |
| 3.4 | 0.999663 | 0.999675 | 0.999687 | 0.999698 | 0.999709 | 0.999720 | 0.999730 | 0.999740 | 0.999749 | 0.999760 |
| 3.5 | 0.999767 | 0.999776 | 0.999784 | 0.999792 | 0.999800 | 0.999807 | 0.999815 | 0.999822 | 0.999828 | 0.999885 |
| 3.6 | 0.999841 | 0.999847 | 0.999853 | 0.999858 | 0.999864 | 0.999869 | 0.999874 | 0.999879 | 0.999883 | 0.999880 |
| 3.7 | 0.999892 | 0.999896 | 0.999900 | 0.999904 | 0.999908 | 0.999912 | 0.999915 | 0.999918 | 0.999922 | 0.999926 |
| 3.8 | 0.999928 | 0.999931 | 0.999933 | 0.999936 | 0.999938 | 0.999941 | 0.999943 | 0.999946 | 0.999948 | 0.999950 |
| 3.9 | 0.999952 | 0.999954 | 0.999956 | 0.999958 | 0.999959 | 0.999961 | 0.999963 | 0.999964 | 0.999966 | 0.999967 |
| 4 | 0.999968 | 0.999970 | 0.999971 | 0.999972 | 0.999973 | 0.999974 | 0.999975 | 0.999976 | 0.999977 | 0.999978 |
| 4.1 | 0.999979 | 0.999980 | 0.999981 | 0.999982 | 0.999983 | 0.999983 | 0.999984 | 0.999985 | 0.999985 | 0.999986 |
| 4.2 | 0.999987 | 0.999987 | 0.999988 | 0.999988 | 0.999989 | 0.999989 | 0.999990 | 0.999990 | 0.999991 | 0.999991 |
| 4.3 | 0.999991 | 0.999992 | 0.999992 | 0.999930 | 0.999993 | 0.999993 | 0.999993 | 0.999994 | 0.999994 | 0.999994 |
| 4.4 | 0.999995 | 0.999995 | 0.999995 | 0.999995 | 0.999996 | 0.999996 | 0.999996 | 1.000000 | 0.999996 | 0.999996 |
| 4.5 | 0.999997 | 0.999997 | 0.999997 | 0.999997 | 0.999997 | 0.999997 | 0.999997 | 0.999998 | 0.999998 | 0.999998 |
| 4.6 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999999 | 0.999999 |
| 4.7 | 0.999999 | 0.999999 | 0.999999 | 0.999999 | 0.999999 | 0.999999 | 0.999999 | 0.999999 | 0.999999 | 0.999999 |
| 4.8 | 0.999999 | 0.999999 | 0.999999 | 0.999999 | 0.999999 | 0.999999 | 0.999999 | 0.999999 | 0.999999 | 0.999999 |
| 4.9 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
| 标准正态分布函数数值表(形式2:sum=0) | ||||||||||||||||||||
| φ(x) x | 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 | ||||||||||
| x | ||||||||||||||||||||
| 0 | 0 | 0.008 | 0.016 | 0.024 | 0.032 | 0.0398 | 0.0478 | 0.0558 | 0.0638 | 0.0718 | ||||||||||
| 0.1 | 0.0796 | 0.0876 | 0.0956 | 0.1034 | 0.1114 | 0.1192 | 0.1272 | 0.135 | 0.1428 | 0.1506 | ||||||||||
| 0.2 | 0.1586 | 0.1664 | 0.1742 | 0.182 | 0.1896 | 0.1974 | 0.2052 | 0.2128 | 0.2206 | 0.2282 | ||||||||||
| 0.3 | 0.2358 | 0.2434 | 0.251 | 0.2586 | 0.2662 | 0.2736 | 0.2812 | 0.2886 | 0.296 | 0.3034 | ||||||||||
| 0.4 | 0.3108 | 0.3182 | 0.3256 | 0.3328 | 0.34 | 0.3472 | 0.3544 | 0.3616 | 0.3688 | 0.3758 | ||||||||||
| 0.5 | 0.383 | 0.39 | 0.397 | 0.4038 | 0.4108 | 0.4176 | 0.4246 | 0.4314 | 0.438 | 0.4448 | ||||||||||
| 0.6 | 0.4514 | 0.4582 | 0.4648 | 0.4714 | 0.4778 | 0.4844 | 0.4908 | 0.4972 | 0.5034 | 0.5098 | ||||||||||
| 0.7 | 0.516 | 0.5222 | 0.5284 | 0.5346 | 0.5406 | 0.5468 | 0.5528 | 0.5588 | 0.5646 | 0.5704 | ||||||||||
| 0.8 | 0.5762 | 0.582 | 0.5878 | 0.5934 | 0.599 | 0.6046 | 0.6102 | 0.6156 | 0.6212 | 0.6266 | ||||||||||
| 0.9 | 0.6318 | 0.6372 | 0.6424 | 0.6476 | 0.6528 | 0.6578 | 0.663 | 0.668 | 0.673 | 0.6778 | ||||||||||
| 1 | 0.6826 | 0.6876 | 0.6922 | 0.697 | 0.7016 | 0.7062 | 0.7108 | 0.7154 | 0.7198 | 0.7242 | ||||||||||
| 1.1 | 0.7286 | 0.733 | 0.7372 | 0.7416 | 0.7458 | 0.7498 | 0.754 | 0.758 | 0.762 | 0.766 | ||||||||||
| 1.2 | 0.7698 | 0.7738 | 0.7776 | 0.7814 | 0.785 | 0.7888 | 0.7924 | 0.796 | 0.7994 | 0.803 | ||||||||||
| 1.3 | 0.8064 | 0.8098 | 0.8132 | 0.8164 | 0.8198 | 0.823 | 0.8262 | 0.8294 | 0.8324 | 0.8354 | ||||||||||
| 1.4 | 0.8384 | 0.8414 | 0.8444 | 0.8472 | 0.8502 | 0.853 | 0.8556 | 0.8584 | 0.8612 | 0.8638 | ||||||||||
| 1.5 | 0.8664 | 0.869 | 0.8714 | 0.874 | 0.8764 | 0.8788 | 0.8812 | 0.8836 | 0.886 | 0.8882 | ||||||||||
| 1.6 | 0.8904 | 0.8926 | 0.8948 | 0.8968 | 0.899 | 0.901 | 0.903 | 0.905 | 0.907 | 0.909 | ||||||||||
| 1.7 | 0.9108 | 0.9128 | 0.9146 | 0.9164 | 0.9182 | 0.9198 | 0.9216 | 0.9232 | 0.925 | 0.9266 | ||||||||||
| 1.8 | 0.9282 | 0.9296 | 0.9312 | 0.9328 | 0.9342 | 0.9356 | 0.9372 | 0.9386 | 0.94 | 0.9412 | ||||||||||
| 1.9 | 0.9426 | 0.9438 | 0.9452 | 0.9464 | 0.9476 | 0.9488 | 0.95 | 0.9512 | 0.9524 | 0.9534 | ||||||||||
| 2 | 0.9544 | 0.9556 | 0.9566 | 0.9576 | 0.9586 | 0.9596 | 0.9606 | 0.9616 | 0.9624 | 0.9634 | ||||||||||
| 2.1 | 0.9642 | 0.9652 | 0.966 | 0.9668 | 0.9676 | 0.9684 | 0.9692 | 0.97 | 0.9708 | 0.9714 | ||||||||||
| 2.2 | 0.9722 | 0.9728 | 0.9736 | 0.9742 | 0.9748 | 0.9756 | 0.9762 | 0.9768 | 0.9774 | 0.978 | ||||||||||
| 2.3 | 0.9786 | 0.9792 | 0.9796 | 0.9802 | 0.9808 | 0.9812 | 0.9818 | 0.9822 | 0.9826 | 0.9832 | ||||||||||
| 2.4 | 0.9836 | 0.984 | 0.9844 | 0.985 | 0.9854 | 0.9858 | 0.9862 | 0.9864 | 0.9868 | 0.9872 | ||||||||||
| 2.5 | 0.9876 | 0.988 | 0.9882 | 0.9886 | 0.989 | 0.9892 | 0.9896 | 0.9898 | 0.9902 | 0.9904 | ||||||||||
| 2.6 | 0.9906 | 0.991 | 0.9912 | 0.9914 | 0.9918 | 0.992 | 0.9922 | 0.9924 | 0.9926 | 0.9928 | ||||||||||
| 2.7 | 0.993 | 0.9932 | 0.9934 | 0.9936 | 0.9938 | 0.994 | 0.9942 | 0.9944 | 0.9946 | 0.9948 | ||||||||||
| 2.8 | 0.9948 | 0.995 | 0.9952 | 0.9954 | 0.9954 | 0.9956 | 0.9958 | 0.9958 | 0.996 | 0.9962 | ||||||||||
| 2.9 | 0.9962 | 0.9964 | 0.9964 | 0.9966 | 0.9968 | 0.9968 | 0.997 | 0.997 | 0.9972 | 0.9972 | ||||||||||
| 3 | 0.9974 | 0.998 | 0.9986 | 0.999 | 0.9994 | 0.9996 | 0.9996 | 0.9998 | 0.9998 | 1 | ||||||||||
| 3.1 | 0.998064 | 0.99813 | 0.998192 | 0.998252 | 0.99831 | 0.998368 | 0.998422 | 0.998476 | 0.998528 | 0.998578 | ||||||||||
| 3.2 | 0.998626 | 0.998672 | 0.998718 | 0.998762 | 0.998804 | 0.998846 | 0.998886 | 0.998924 | 0.998962 | 0.998998 | ||||||||||
| 3.3 | 0.999034 | 0.999068 | 0.9991 | 0.999132 | 0.999162 | 0.999192 | 0.99922 | 0.999248 | 0.999276 | 0.99932 | ||||||||||
| 3.4 | 0.999326 | 0.99935 | 0.999374 | 0.999396 | 0.999418 | 0.99944 | 0.99946 | 0.99948 | 0.999498 | 0.99952 | ||||||||||
| 3.5 | 0.999534 | 0.999552 | 0.999568 | 0.999584 | 0.9996 | 0.999614 | 0.99963 | 0.999644 | 0.999656 | 0.99977 | ||||||||||
| 3.6 | 0.999682 | 0.999694 | 0.999706 | 0.999716 | 0.999728 | 0.999738 | 0.999748 | 0.999758 | 0.999766 | 0.99976 | ||||||||||
| 3.7 | 0.999784 | 0.999792 | 0.9998 | 0.999808 | 0.999816 | 0.999824 | 0.99983 | 0.999836 | 0.999844 | 0.999852 | ||||||||||
| 3.8 | 0.999856 | 0.999862 | 0.999866 | 0.999872 | 0.999876 | 0.999882 | 0.999886 | 0.999892 | 0.999896 | 0.9999 | ||||||||||
| 3.9 | 0.999904 | 0.999908 | 0.999912 | 0.999916 | 0.999918 | 0.999922 | 0.999926 | 0.999928 | 0.999932 | 0.999934 | ||||||||||
| 4 | 0.999936 | 0.99994 | 0.999942 | 0.999944 | 0.999946 | 0.999948 | 0.99995 | 0.999952 | 0.999954 | 0.999956 | ||||||||||
| 4.1 | 0.999958 | 0.99996 | 0.999962 | 0.999964 | 0.999966 | 0.999966 | 0.999968 | 0.99997 | 0.99997 | 0.999972 | ||||||||||
| 4.2 | 0.999974 | 0.999974 | 0.999976 | 0.999976 | 0.999978 | 0.999978 | 0.99998 | 0.99998 | 0.999982 | 0.999982 | ||||||||||
| 4.3 | 0.999982 | 0.999984 | 0.999984 | 0.99986 | 0.999986 | 0.999986 | 0.999986 | 0.999988 | 0.999988 | 0.999988 | ||||||||||
| 4.4 | 0.99999 | 0.99999 | 0.99999 | 0.99999 | 0.999992 | 0.999992 | 0.999992 | 0.9999992 | 0.999992 | 0.999992 | ||||||||||
| 4.5 | 0.999994 | 0.999994 | 0.999994 | 0.999994 | 0.999994 | 0.999994 | 0.999994 | 0.999996 | 0.999996 | 0.999996 | ||||||||||
| 4.6 | 0.999996 | 0.999996 | 0.999996 | 0.999996 | 0.999996 | 0.999996 | 0.999996 | 0.999996 | 0.999998 | 0.999998 | ||||||||||
| 4.7 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | ||||||||||
| 4.8 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | 0.999998 | ||||||||||
| 4.9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||
ref: 正态分布的由来
[高斯分布-笔记(1) ]












![\Phi(z)=\frac12 \left[1 + \mathrm{erf}\,(\frac{z-\mu}{\sigma\sqrt2})\right] .](http://upload.wikimedia.org/wikipedia/zh/math/3/0/9/309df22a79a5687e1891cfbcbae2db89.png)

![\Phi(z)=\frac{1}{2} \left[ 1 + \operatorname{erf} \left( \frac{z}{\sqrt{2}} \right) \right].](http://upload.wikimedia.org/wikipedia/zh/math/d/0/5/d052159a00aa278a29d101a5c2b59353.png)
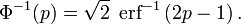





























 3968
3968

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








