在支持向量机模型的求解中,我们用到了SMO算法来求解向量α。那么什么是SMO算法?在讲SMO算法之前,我们需要先了解以下坐标上升法。
1、坐标上升法
假设有优化问题:
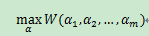

算法的思想为:每次只考虑一个变量进行优化,将其他变量固定。这时整个函数可以看作只关于该变量的函数,可以对其直接求导计算。然后继续求其他分变量的值,整个内循环下来就得到了α的一组值,若该组值满足条件,即为我们求的值,否则继续迭代计算直至收敛。一个示意图如下:
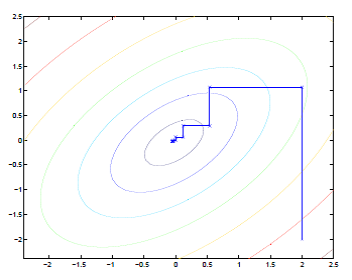
如图为一个二次椭圆曲线的等高线,变量维数为2,初始值在点(2,-2),可见其优化路径为折线式前进,因为算法每次只在一个方向上对函数进行优化。
2、SMO算法
在讲支持向量机求目标函数最优时,通过求解对偶问题转换为求解目标函数对α的极大值,如下:
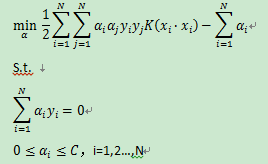
可以看到优化问题与上面提到的坐标上升法很相似,参考上面讲到的坐标上升法,我们也可以选择向量α的一个变量








 本文介绍了SMO算法在支持向量机中的应用,首先讲解了坐标上升法,然后详细阐述了SMO算法如何解决对偶问题,通过选择变量并满足KKT条件来更新α。SMO算法采用启发式方法选择变量,确保目标函数在迭代后能有效降低,最后提到了阈值b的更新策略。对于SMO的深入学习,建议参考Andrew ng的课程和John C.Platt的论文。
本文介绍了SMO算法在支持向量机中的应用,首先讲解了坐标上升法,然后详细阐述了SMO算法如何解决对偶问题,通过选择变量并满足KKT条件来更新α。SMO算法采用启发式方法选择变量,确保目标函数在迭代后能有效降低,最后提到了阈值b的更新策略。对于SMO的深入学习,建议参考Andrew ng的课程和John C.Platt的论文。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 3798
3798

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








