漫步微积分六——极限的概念

前面给出的导数定义都依赖于函数极限的概念，我们对极限只做了最简短的解释。现在，我们已经知道了这一概念的目的，接下来关心一下它的意义。

考虑函数$f(x)$，自变量在点$a$的领域内都有定义，但是$a$ 点本身没定义。假设存在一个实数值$L$，当$x$越来越接近$a$时，$f(x)$越来越接近$L$(图1)。对于这种情况我们说$L$是$x$趋近$a$时$f(x)$的极限，用符号表示为

$$\begin{equation} \lim_{x\to a}f(x)=L.\tag1 \end{equation}$$

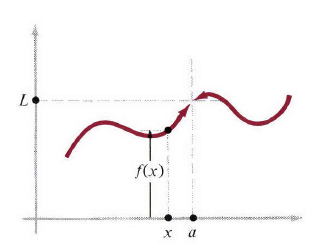
图1

如果不存在这样的实数 $L$，我们说$x$趋近 $a$时$f(x)$没有极限，或者 $\lim_{x\to a}f(x)$ 不存在。另一种和(1)等价且被广泛使用的符号是
$$f(x)\to L\quad as \quad x\to a$$ 现在考虑(1)式的意义， $x$等于$a$时 $f(x)$会如何是没有意义的；而对于 $x$接近$a$时的 $f(x)$值才是有意义的，理解这一点非常重要。

对于(1)式来说，这些非正式的描述对我们直观的理解非常有利，并且对于实际需求也足够了。然而，作为定义，他们又不严谨也不精确，因为有越来越接近和趋近这样的含糊用语。(1)式的精确意义非常重要，所以我们不能只留给学生去想象。我们尽可能简洁又清晰的给出一个令人满意的定义。接下来的部分，阅读的时候最好比平时更仔细些，及饬令他们自然的不耐烦用什么似乎是过度的挑剔的精度。

首先分析一个具体的实例，希望从中可以提取出通用情况的本质

$$\lim_{x\to 0}\frac{2x^2+x}{x}=1$$ 这里我们必须验证的函数是
$$y=f(x)=\frac{2x^2+x}{x}$$ 这个函数在 $x=0$处无定义，除了 $x\neq 0$外的所有 $x$，化简表达式的
$$f(x)=\frac{x(2x+1)}{x}=2x+1.$$ 从图2中，我们可以清楚的看到，当 $x$趋近于$0$时， $f(x)$ 趋近于 $1$。为了给出定量的描述，我们需要$f(x)$与极限值 $1$之差的公式：
$$f(x)-1=(2x+1)-1=2x.$$

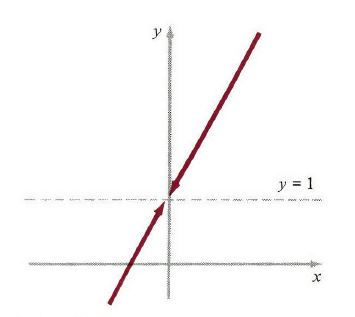
图2

从公式中可以看到 $f(x)$可以越来越接近 $1$，也就是说，当$x$无线靠近 $0$时，这个差可以变得任意小。
$$\begin{eqnarray*} f(x)-1 &=&\frac{1}{100}\ \ \qquad when\qquad x=\frac{1}{200}\\ f(x)-1 &=&\frac{1}{1000}\qquad when\qquad x=\frac{1}{2000} \end{eqnarray*}$$ 更一般的，让 $\epsilon$是任意正数，无论多小，定义 $\delta$为它的一半 $\delta =\frac{1}{2}\epsilon$。那么当 $x$和$0$的距离小于 $\delta$时， $f(x)$到 $1$的距离将小于$\epsilon$；也就是
$$if\quad |x|<\delta =\frac{1}{2}\epsilon\quad then\quad |f(x)-1|=2|x|<\epsilon .$$ 这个说法比 $x$趋近$0$时 $f(x)$趋近 $1$的模糊说法更精确。它精确地告诉我们$x$必须接近 $0$到什么程度时，才能保证$f(x)$ 靠近 $1$的程度。当然，$x$不能等于 $0$，因为$x=0$处 $f(x)$没意义。

现在这个$\epsilon -\delta$定义应该很容易掌握了:对于任意一个正数$\epsilon$，存在一个正数$\delta$，使得

$$|f(x)-L|<\epsilon$$ 其中 $x\neq a$，且满足不等式
$$|x-a|<\delta$$ 换句话说：如果给定一个 $\epsilon >0$，那么可以找到这样的一个正数 $\delta$，满足当 $x$在$a$的 $\delta$邻域内时， $f(x)$将在 $L$的$\epsilon$邻域内。跟之前一样，我们只关心 $x=a$附近的 $f(x)$行为，不在乎 $x=a$处发生什么。

用函数$y=f(x)$的图像来解释这个想法会更直观一些，如图3。图中，$2\epsilon$是水平带的宽度，它的中心线是$y=L$，$2\delta$是垂直带的宽度，它的中心线是$x=a$，上面的定义可以表达为

对于每条水平带，无论它多窄，存在这样的一条垂直带，如果$x\neq a$限定在垂直带内，那么对应部分限定在水平带内。

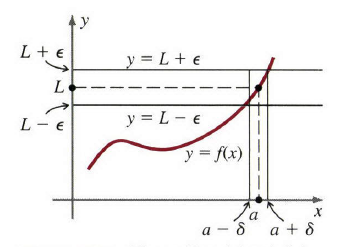
图3

(1)式的精确定义应该是我们最关注的，并且它在微积分理论中扮演着重要的角色。但是，对于极限直观的理解足够满足我们的实际需要，从这个层面来说，下面的例子现在应该不难解决了。

例1：首先

$$\lim_{x\to 2}(3x+4)=10$$ 当 $x$趋近$2$时， $3x$趋近 $6$，$3x+4$趋近 $6+4=10$。下一个
$$\lim_{x\to 1}\frac{x^2-1}{x-1}=\lim_{x\to 1}\frac{(x+1)(x-1)}{x-1}=\lim_{x\to 1}(x+1)=2$$ 我们首先注意到函数 $(x^2-1)/(x-1)$在 $x=1$处没有定义，因为此时分子分母均等于 $0$。但是这无关紧要，因为重要的是$x$在 $1$附近而不是$1$处的函数行为，所以对所有 $x$均可进行消去操作，得到$x+1$，它趋近 $2$。

例2：考虑一些极限不存在的函数是非常有启发意义的。例如图4，这些极限行为通过图像都很容易理解。第一种情况，当$x$为正数时，函数等于 $1$，当$x$为负数时，函数等于 $-1$，在 $x=0$处没有定义，所以当 $x$趋近$0$时，函数不存在一个确定的数。专业点来说就是极限不存在，记为

$$\lim_{x\to 0+}\frac{x}{|x|}=1\qquad \lim_{x\to 0-}\frac{x}{|x|}=-1.$$

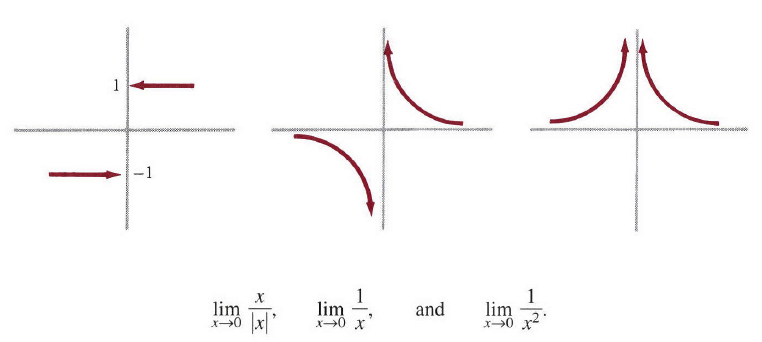
图4

符号 $x\to 0+$和 $x\to 0-$表明变量 $x$分别从正向(右边)和反向(左边)趋近$0$。另外两个极限因为 $x$趋近$0$时绝对值任意大所以也不存在极限。用符号表示就是
$$\lim_{x\to 0+}\frac{1}{x}=\infty ,\quad \lim_{x\to 0-}\frac{1}{x}=-\infty ,\quad \lim_{x\to 0}\frac{1}{x^2}=\infty.$$ 记住：(1)式中的数 $L$必须是实数；$L=\infty$不符合要求。

计算极限的主要规则就是我们期待的那样。例如

$$\lim_{x\to a}x=a;$$ 如果 $c$是常数，那么
$$\lim_{x\to a}c=c.$$ 还有，如果 $\lim_{x\to a}f(x)=L$， $\lim_{x\to a}g(x)=M$，那么
$$\begin{eqnarray*} \lim_{x\to a}[f(x)+g(x)] &=&L+M,\\ \lim_{x\to a}[f(x)-g(x)] &=&L-M,\\ \lim_{x\to a}f(x)g(x) &=&LM,\\ \lim_{x\to a}\frac{f(x)}{g(x)} &=&\frac{L}{M}\quad (M\neq 0). \end{eqnarray*}$$ 也就是说，和的极限是极限的和，差，乘和商同样满足。这些叫做极限法则或者极限定理。

我们之前说过微积分是解决问题的一种技能，不是逻辑的分支。相比于演绎推理，它更多的是处理直观理解带来的方法。当然了，我们将试图让读者相信我们论述的真实性和过程的合法性。然而，为了避免用大量难理解的理论材料充斥文本，我们尽可能简洁，不那么正式的表达。（对于这里陈述的极限性质，相关证明可能以番外的形式给出，至于是否更新，还是看呼声吧，哈哈哈）

在结束本部分主题之前，我们讨论两个具体的三角极限。之后会发现他们非常重要。第一个是

$$\begin{equation} \lim_{\theta\to 0}\frac{sin\theta}{\theta}\tag2 \end{equation}$$
注意，这里的 $\theta$是弧度。我们不能简单的设 $\theta =0$，因为结果将是无意义的等式 $0/0$。我们注意到它不同于下面的代数极限，
$$\lim_{x\to 0}\frac{3x^2+2x}{x}=\lim_{x\to 0}\frac{x(3x+2)}{x}=\lim_{x\to 0}(3x+2)=2$$ 因为 $sin\theta$无法明显的消去 $\theta$。为了对(2)式的函数行为有个印象，我们计算几个很小的 $\theta$对应的比值。我们注意到，如果用 $-\theta$代替 $\theta$，我们有
$$\frac{sin -\theta}{-\theta}=\frac{-sin\theta}{-\theta}=\frac{sin\theta}{\theta}$$ 所以我们只关于正的 $\theta$。利用计算器我们得到几个八位小数值(表1)。这些值说明(但不能证明!)

表1

$$\begin{equation} \lim_{\theta\to 0}\frac{sin\theta}{\theta}=1.\tag3 \end{equation}$$ 现在我们从几何角度来证实(3)式。让 $P$，$Q$是单位圆上彼此濒临的两个点(图5)，让 $\overline{PQ}$和 $\widehat{PQ}$表示两点的弦长和弧长。那么当两点移动到一起时，弦长比弧长趋近于 $1$
$$\frac{chord\ length\ \overline{PQ}}{arc\ length\ \widehat{PQ}}\to 1\quad as\quad \widehat{PQ}\to 0.$$

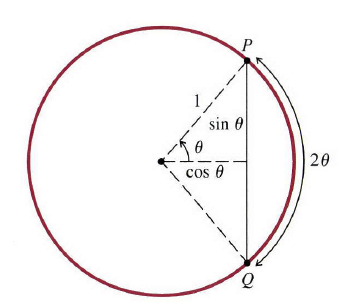
图5

对于图中的符号，这个几何陈述等价于
$$\frac{2sin\theta}{2\theta}=\frac{sin\theta}{\theta}\to 1\quad as\quad 2\theta \to 0\quad or\quad \theta\to 0,$$ 这就是(3)式。

第二个极限是

$$\begin{equation} \lim_{\theta\to 0}\frac{1-cos\theta}{\theta}=0.\tag4 \end{equation}$$ 利用三角恒等式 $sin^2\theta+cos^2\theta=1$以及(3)式得：
$$\begin{eqnarray*} \lim_{\theta\to 0}\frac{1-cos\theta}{\theta} &=&\lim_{\theta\to 0}\left(\frac{1-cos\theta}{\theta}\cdot\frac{1+cos\theta}{1+cos\theta}\right)\\ &=&\lim_{\theta\to 0}\frac{1-cos^2\theta}{\theta(1+cos\theta)}\\ &=&\lim_{\theta\to 0}\frac{sin^2\theta}{\theta(1+cos\theta)}\\ &=&\lim_{\theta\to 0}\left(\frac{sin\theta}{\theta}\cdot\frac{sin\theta}{1+cos\theta}\right)\\ &=&\left(\lim_{\theta\to 0}\frac{sin\theta}{\theta}\right)\left(\frac{sin\theta}{1+cos\theta}\right)\\ &=&1\cdot\frac{0}{1+1}=0. \end{eqnarray*}$$ 最后一步用到了当 $\theta\to 0$时 $sin\theta\to 0$， $cos\theta\to 1$，从图5的 $sin\theta$和 $cos\theta$几何意义可以很容易证实他们。