概率论与数理统计————古典概型、几何概型和条件概率

辣个骑士

已于 2024-01-15 17:37:45 修改

阅读量4.4k

点赞数 10

分类专栏：概率论与数理统计文章标签：概率论

于 2024-01-15 15:28:50 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/2201_75333727/article/details/135601054

版权

概率论与数理统计专栏收录该内容

3 篇文章

订阅专栏

本文概述了概率论中的关键概念，包括古典概型的有限性和等可能性、几何概型的计算公式、条件概率的定义以及全概率公式和贝叶斯公式的应用，还介绍了伯努利试验及其在二项式概率中的运用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、古典概型

特点

（1）有限性：试验S的样本空间的有限集合

（2）等可能性：每个样本点发生的概率是相等的

公式：P（A）= $\frac{A}{S}$ A为随机事件的样本点数；S是样本空间

二、几何概型

计算公式：p（A）= $\frac{A}{S}$ A的长度、面积或体积 S的长度、面积或体积

三、条件概率

条件概率：设A、B为两个事件，且p（B）>0,则在事件B条件下事件A发生的概率为

P（A|B）= $\frac{P(AB)}{P(B)}$

p（ $\bar{B}$ |A）=1-P（B|A）

乘法公式：

事件的独立性：若事件A、B满足P（B|A）=P（B）则事件A、B相互独立

本质：A和B互不影响

A、B相互独立——>P（AB）=P（A）P（B）

三事件相互独立：

四、全概率公式和贝叶斯公式

完备事件组：（1）A1、A2、A3、.....、An两两互斥（2） $A1\cup A2\cup A3\cup .....\cup An$ =S

则称A1A2A3An为完备事件组，或者一个划分

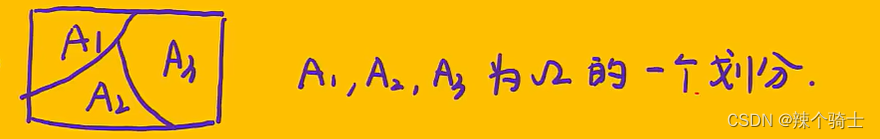
全概率公式：设B事件为任意事件，A1、A2、A3、.......、An为完备事件组

P（B）=P（A1)P(B|A1)+P(A2)P(B|A2)+,,,,,,,,,+P(An）P（B|An）

贝叶斯公式：设B事件为任意事件，A1、A2、A3、.......、An为完备事件组

P（Ai|B）= $\frac{AiB}{B}$ = $\frac{p(Ai)P(B|Ai)}{\sum P(Ai)P(B|Ai)}$

五、伯努利试验和伯努利概型

伯努利试验：试验S只有两种结果A和 $\bar{A}$

n重伯努利试验：把伯努利试验重复进行n次

二项式概率公式: $Pn(k)=C_{n}^{k} p^{k} (1-p)^{n-k}$

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

打赏作者

辣个骑士 你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20

扫码支付：¥1

获取中

扫码支付

您的余额不足，请更换扫码支付或充值

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。