主成分分析(相关矩阵)-SPSS

一、实验环境

1、SPSS 25.0

2、Windows X64

二、实验内容

实验数据：

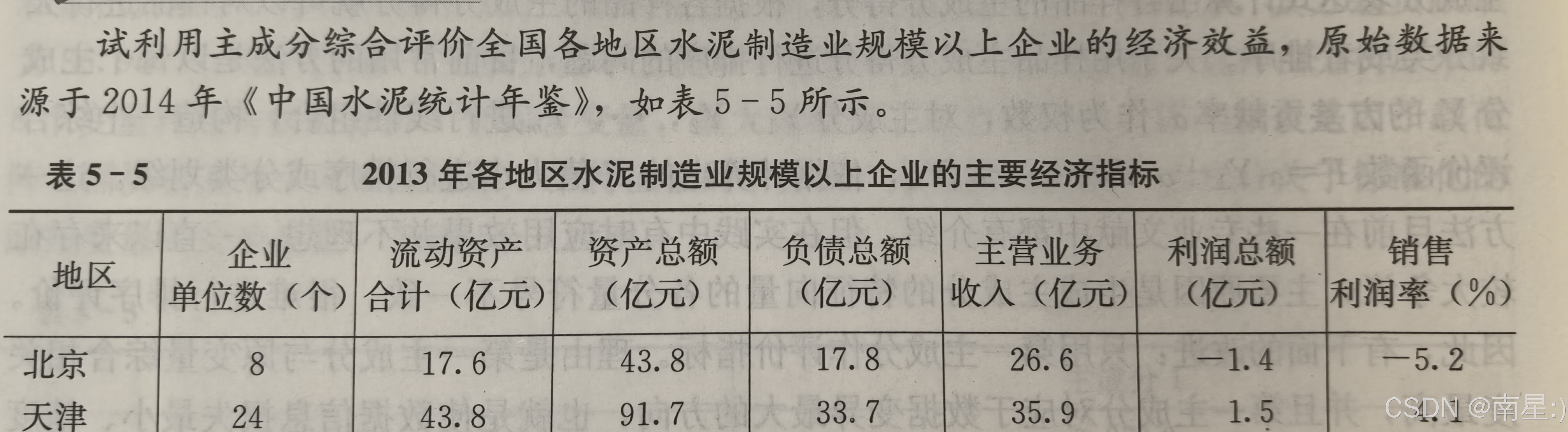
实验步骤：

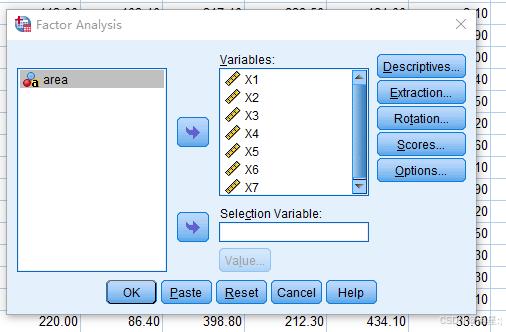
将7个指标变量选入类别放入Variables框中。

一般而言，对于度量单位不同的指标或是取值范围彼此差异非常大的指标，我们应该考虑将数据标准化，由相关矩阵出发求解主成分。对同度量或是取值范围在同量级的数据，为保证数据信息的完整性从协方差矩阵求解主成分为宜。由于本题指标的度量单位不同，因此本题用相关矩阵出发求解主成分。

结果分析：

由上图可以看出除了X7与各变量的相关性不强以外，其它变量之间均存在较强的相关关系，因此原始数据适合做主成分分析。

该检验的原假设是相关系数矩阵为单位阵，由上图可知显著性小于0.05，因此判断拒绝原假设，由此说明原始数据适合做主成分分析。

由上图可以看出从协方差矩阵出发求解主成分结果保留了前两个主成分，第一主成分的方差贡献率为73.763%，第二主成分的方差贡献率为17.273%，所以两个主成分解释了全部变量总方差的91.036%，由此说明2个主成分代表原来的7个指标评价企业的经济利益已经足够。

对component1和component2对应两列元素分别除以如下图的特征根的平方根。

根据上述计算结果，可得到两个主成分的线性表达式：

其中，表示对原始变量标准化后的变量。