第十二周调研方法学习——问卷分析方法

第十二周调研方法学习——问卷分析方法

声明：本篇博客旨在为未接触过概统学习的，但需要进行问卷分析的同学提供一些理解性质的解读，中间许多表述并不严谨，同学们还应该系统地学习概率论与数理统计。

数学期望和概率密度函数

数学期望：

数学期望是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一，它反映随机变量平均取值的大小。

对于离散随机变量，期望值是每个可能值乘以其发生的概率的总和。比如我掷一枚硬币，记正面朝上为$+1$，反面朝上为$-1$，它们发生的概率均为$0.5$，那么期望就为$1\times 0.5+(-1)\times 0.5=0$。

而对于连续随机变量，期望值是函数值乘以其概率密度函数在整个定义域上的积分。

概率密度函数

那么，什么是概率密度函数呢？在处理连续随机变量时，我们关注的是随机变量落在某个区间内的概率，而不是它取某个具体值的概率。而概率密度是在概率论中用来描述连续随机变量在某个特定取值附近的概率分布的密度。

对于连续随机变量X，概率密度函数f(x)描述的是X取某个特定值或者落入某个很小区间内的概率。具体来说，f(x)在某一点x处的值并不直接代表X等于x的概率，因为对于连续随机变量来说，X等于任何一个具体值的概率实际上是0。相反，f(x)在某一点x处的值代表的是X落在x附近的一个小范围内的概率与这个范围大小的比值（当这个范围趋近于0时）。

我们可以用线密度来类比去理解概率密度函数。想象一下，如果你有一根线，它的线密度函数$\lambda (x)$随位置x变化。这意味着在不同的位置，单位长度的线质量是不同的。如果你想要计算从x=a到x=b这段线段的总质量，你会对线密度函数进行积分：

$M(a,b)={\int }_a^b\lambda (x)dx$

这个积分会给你在a和b之间的线段总质量。

同样地，对于概率密度函数f(x)，如果你想要计算连续随机变量X落在某个区间[a, b]内的概率，你会对概率密度函数进行积分：

$P(a<X<b)={\int }_a^{b}f(x)dx$

这个积分会给你X落在区间[a, b]内的概率。

由概率密度函数的定义，我们可以看出概率密度函数必须满足两个基本条件：
1.非负性：对于所有的x，f(x) ≥ 0。
2.归一性：X在整个定义域上的概率密度函数的积分等于1，即 ${\int }_a^{b}f(x)dx$。
在连续分布中，正态分布（也称为高斯分布）是统计学中最重要的概率分布之一。因为正态分布能够很好地模拟和描述许多自然现象。

正态分布的概率密度函数为
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)$$
其中$\mu$为均值，$\sigma$为方差。正态分布的概率密度函数仅有均值和方差两个参数，因此如果两组数据均满足正态分布，我们要想判断两组数组是否具有差异，就只需要比较这两组数据的均值和方差是否相同。这就涉及到了差异性分析的部分内容。

假设检验

假设检验是一种统计方法，用于评估样本数据是否支持某个假设。这个假设通常是关于总体参数的，例如总体均值、总体比例等。假设检验的主要目的是确定观察到的数据是否足够强有力地支持或拒绝这个假设。

假说检验的步骤如下：
1.提出假设：研究者首先提出一个关于总体参数的假设，通常包括零假设，也称为原假设（H0）和备择假设（H1）。
零假设 是指研究人员假定为真的某种假设，通常表达为总体参数等于某个固定值。例如，零假设可以是“这个群体的平均年龄是50岁”，“这个药物对治疗癌症没有作用”等等。
备择假设 则是对零假设的否定或补充，通常表达为总体参数不等于或大于或小于某个固定值。例如，“这个群体的平均年龄不是50岁”，“这个药物对治疗癌症有一定的有效性”等等。

2.收集样本数据：从总体中抽取样本，并收集相关的数据。

3.计算检验统计量：使用样本数据计算一个统计量，这个统计量应该在零假设为真时具有某种分布。

4.确定显著性水平：显著性水平是指当原假设为正确时人们却把它拒绝了的概率或风险。它是公认的小概率事件的概率值，必须在每一次统计检验之前确定，通常取α=0.05或α=0.01。这表明，当作出接受原假设的决定时，其正确的可能性（概率）为95%或99%。
选择一个显著性水平（通常为0.05或0.01），用于确定拒绝零假设的阈值。

5.确定临界值或p值：根据显著性水平和检验统计量的分布，确定临界值或计算p值。
6.做出决策：根据临界值和p值，决定是否拒绝零假设。如果p值小于显著性水平，则拒绝零假设；否则，不拒绝零假设。

假说检验中有一个重要的概念——p值，p值（p-value）是一个概率值，它表示在零假设（H0）为真的情况下，观察到或更极端的数据出现的概率。p值是假设检验中的一个关键概念，它帮助我们判断样本数据是否与零假设所描述的总体特征显著不同。换句话说，它可以表示用样本数据得出来的结论出错的概率，比如如果计算出p值为0.05，就意味着这个结论（零假设）由95%的可能性是正确的，如果95%在我们能容忍的范围之内，我们就可以说这个结论是可靠的。

p值的计算方法取决于所进行的假设检验类型。例如独立样本t检验的p值计算公式如下：
$$t=\frac{{\bar{x}}_1-{\bar{x}}_2}{s_{\text{pooled}}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$$
$$p\text{ 值}=P(T>|t|)$$

我们来通过例子来理解假设检验：

示例解释

已知某班级微积分a（2）考试成绩服从正态分布，并估计其平均成绩为75，现从班级中抽取了5位同学，这5位同学的平均成绩为72，问：所估计的75分的平均成绩是否正确？
全班平均成绩75是假设，可以根据实际样本平均成绩72分以及相关定理判断平均成绩75分是否正确，这是检验。
在这个例子中：E(X)=75是原假设 H0，E(X)≠75是备择假设 H1
检验结果 ：接受原假设或拒绝原假设

假设检验提供了科学决策的基础。通过比较数据与某个假设的预期结果，研究者可以决定是否支持或拒绝该假设。注意：假设检验的正确性是在一定显著性水平下而言的，我们不能通过假设检验来判断某一假设是百分百正确的，而是说这一假设正确的概率大于百分之95（当显著性水平为0.05）。

差异性分析

差异性分析是统计学中的一种方法，用于比较两个或多个样本或总体之间的差异。它可以帮助我们确定这些样本或总体是否来自具有相同分布的总体，或者它们的平均值、比例、比例的差异等是否显著不同。

差异性分析在后续数据处理中是非常关键的一环。比如说我们要分析大一和大三学生获取信息的差异，我们就需要对问卷收回来的两组数据进行差异性分析。

差异性分析具有很多种类，当数据满足正态分布时，一般可以直接使用标准假设检验方法（如t检验、ANOVA等）进行差异性分析。如果数据不符合正态分布，可以考虑使用非参数检验方法来进行差异性分析。那么我们如何得知数据是否满足正态分布呢？此时我们就需要对数据进行正态性检验。

正态性检验（Normality Test）是用来判断一组数据是否符合正态分布的统计检验。如果数据不符合正态分布，那么使用基于正态分布假设的统计方法（如t检验、ANOVA等）可能会导致错误的结论。正态性检验有很多种方法，比如S-W检验、K-S检验等。在实际应用中，根据数据的样本量和分布特性，可以选择合适的检验方法。

示例1（参数检验）：如研究不同学校的学生(各学校学生数不一定相等)成绩是否存在差异性。

（来源：spsspro）

数据表：

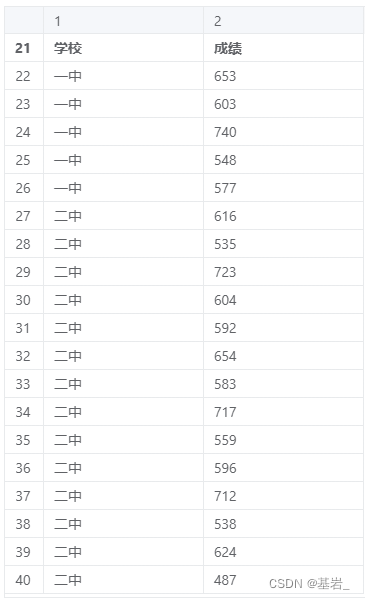
输出结果：

1. 正态性检验结果
   
   图表说明：
   上表展示了定量变量成绩描述性统计和正态性检验的结果，包括中位数、平均值等，用于检验数据的正态性。
   因为成绩的数据量小于 5000，故采用 S-W 检验其正态性，显著性 P 值为 0.496，P 值大于 0.05，水平上不呈现显著性，不能拒绝原假设，因此数据满足正态分布。其峰度（-0.82）绝对值小于 10, 并且偏度（-0.027）绝对值小于 3，可以结合正态分布直方图、PP 图或者 QQ 图进行进一步分析。

2. 正态性检验直方图
   
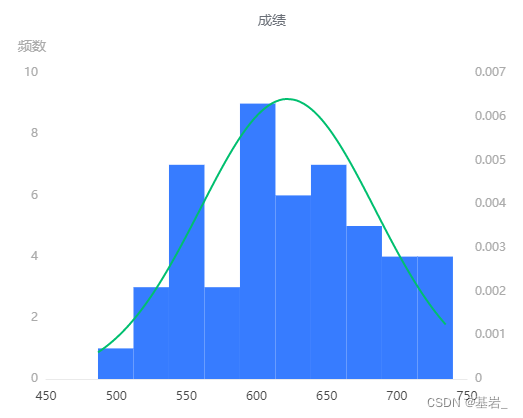
   图表说明：
   如图所示，图片基本呈现钟形（中间高，两端低）的形状，且其峰度绝对值小于 10，偏度绝对值小于 3，故可以认为其具有正态性，故我们可以采用独立样本 T 检验进行检验。

3. 方差齐性检验
   
   图表说明：
   因为独立样本 t 检验需要满足方差齐性，满足方差齐性的数据比较才具有意义，故我们进行方差齐性检验。
   上表展示了方差齐性的结果，包括标准差、F 检验结果、显著性 P 值。方差齐性检验的结果显示, 对于成绩，显著性 P 值为 0.393，水平上不呈现显著性，不能拒绝原假设，因此数据满足方差齐性，可以采用独立样本 t 检验。
   ​

4. 独立样本 T 检验分析结果表
   
   图表说明：
   上表展示了独立样本 T 检验的结果，包括均值 ± 标准差的结果，t 检验结果，显著性 P 值、效应量 Cohen’s d 值。
   一中，二中在成绩上的均值分别为:634.375/610.36，基本差距不大。
   T 检验结果 p 值为 0.18>=0.05,因此统计结果不显著，说明一中的学生和二中的学生的成绩上不存在显著差异。
   且 Cohen’s d 值为 0.389，差异幅度不算大。

示例2（非参数检验）：检验某医院 300 个病人注射某药剂前后血压是否一致（差值非正态分布）

（来源：spsspro）

数据表：

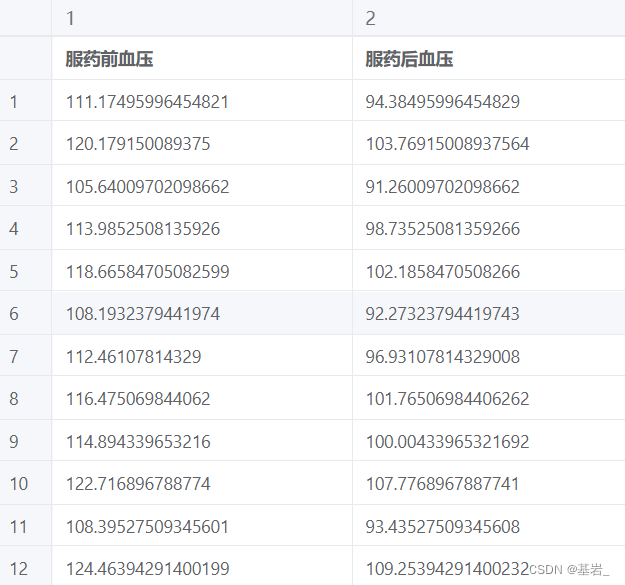
输出结果：

1. 正态性检验结果
   

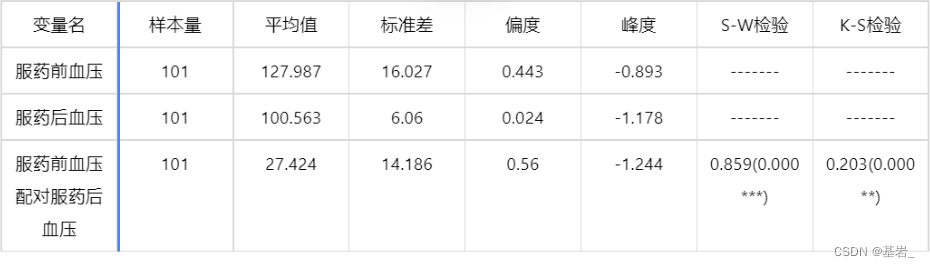
图表说明：
因为服药前血压配对服药后血压的差值样本数量 N≥5000，故采用 K-S 检验检验其正态性，显著性 P 值为 0.000，水平上不呈现显著性，不能拒绝原假设，因此数据不满足正态分布，故进行配对样本 Wilcoxon 符号秩检验。若满足正态分布则进行配对样本 t 检验。
2. 正态性检验直方图

图表说明：
上图展示了定量变量服药前血压、服药后血压的差值数据正态性检验的结果：
由图可得，服药前血压、服药后血压的差值分布明显非正态分布，故进行 Wilcoxon 符号秩检验。

3. 配对样本 Wilcoxon 符号秩检验
   

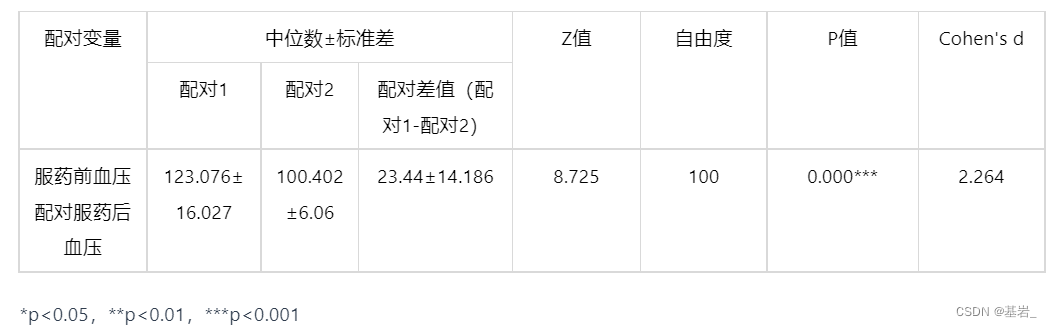
图表说明：
配对样本wilcoxon检验的结果显示，基于字段服药前血压配对服药后血压的差值，显著性P值为0.000，水平上呈现显著性，拒绝原假设，因此服药前血压配对服药后血压之间存在显著性差异。 其差异幅度Cohen’s d值为：2.264，差异幅度非常大。
（小（约 0.2）、中等（约 0.5）和大（约 0.8））

相关性分析

除了差异性分析之外，相关性分析同样是统计学中分析数据的一个重要方法，它是对变量两两之间的相关程度进行分析。相关分析可以帮助我们确定变量之间是否存在相关性，以及它们之间的相关程度和方向。

它的结果通常用相关系数来表示，相关系数的值范围在 -1 到 1 之间，其绝对值越接近 1，表示两个变量之间的相关性越强。

相关分析的计算主要包括皮尔逊相关系数和斯皮尔曼等级相关系数。皮尔逊相关系数适用于两个连续变量之间的线性关系。只有当连续数据，正态分布，线性关系三个条件同时满足时，用皮尔逊相关系数才最为恰当。上述任一条件不满足，就用斯皮尔曼相关系数。因此斯皮尔曼相关系数比皮尔逊相关系数适用的更为广泛。

示例1（Kendall一致性检验）：分析 10 个旅游评论家对 5 个景点的打分一致性程度。

（来源：spsspro）

数据表：

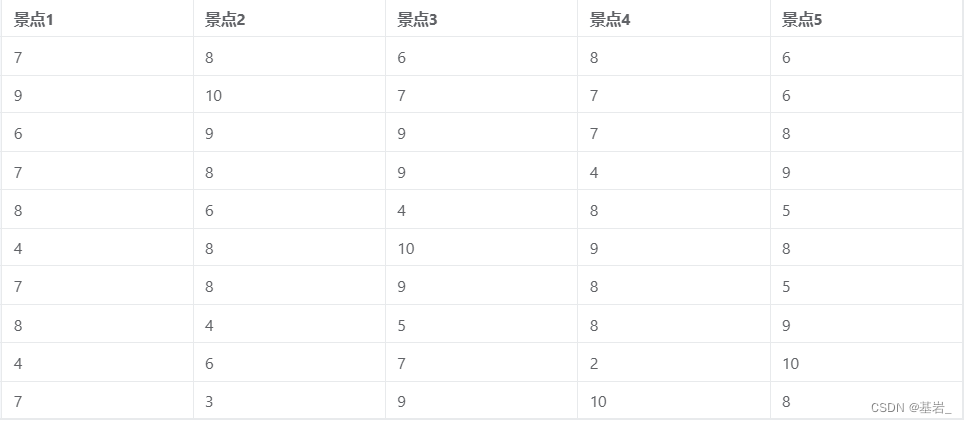
输出结果：

1. Kendall 一致性检验
   

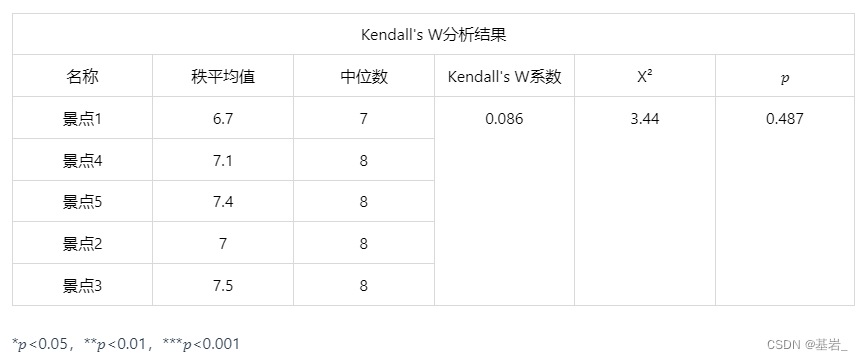
图表说明：
上表展示了模型检验的结果，包括：秩平均值、中位数、Kendall 协调系数 𝑊、卡方值、显著性 𝑝 值；
Kendall 系数一致性检验的结果显示，总体数据的显著性 𝑝 值为 0.487，水平上不呈现显著性，不能拒绝原假设，因此数据不能呈现一致性，同时模型的 Kendall 协调系数 𝑊 值为 0.086，因此相关性的程度为极低的一致性。可见五位评委对景点的评分不具有一致性。

示例2（斯皮尔曼相关性分析）：人的身高、体重、和每周运动时间

（来源：知乎）

数据表：

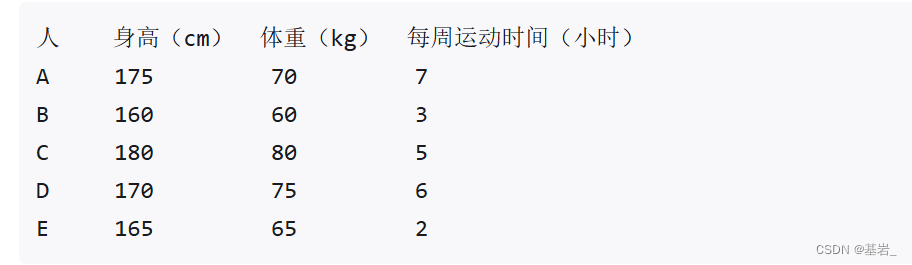
步骤：

1. 排名转换
   

2.计算排名差值和平方差：

3.计算斯皮尔曼相关系数：

对于每对变量，我们分别计算相关系数。例如，身高与体重的斯皮尔曼相关系数：
$$\rho =1-\frac{6\Sigma d_i^2}{n(n^2-1)}=1-\frac{6\times 5}{5(25-1)}=0.75$$

python 代码

import numpy as np
from scipy.stats import spearmanr

# 数据准备
height = [175, 160, 180, 170, 165]
weight = [70, 60, 80, 75, 65]
exercise_time = [7, 3, 5, 6, 2]

# 计算斯皮尔曼相关系数
corr_height_weight, _ = spearmanr(height, weight)
corr_height_exercise, _ = spearmanr(height, exercise_time)
corr_weight_exercise, _ = spearmanr(weight, exercise_time)

print(f"身高与体重的斯皮尔曼相关系数: {corr_height_weight}")
print(f"身高与每周运动时间的斯皮尔曼相关系数: {corr_height_exercise}")
print(f"体重与每周运动时间的斯皮尔曼相关系数: {corr_weight_exercise}")

信度分析

引用自：知乎

上面带大家了解了有关数据分析的一些内容，下面介绍一下问卷分析中的信度分析。

信度 ： 通俗说是：你设计的调查问卷（量表），如果一群人重复去填写n次，每次填写得到的结果是否一致或基本相近？如果是，那么可说该问卷搜集到的数据具有一致性或稳定性，也可以说随机误差小，也就是具有信度。如果不是，则不具有信度。

信度分析主要用来考察问卷中量表所测结果的稳定性以及一致性，即用于检验问卷中量表样本是否可靠可信。

信度分析可以确定样本有没有真实地回答了问题。但是如果我们回收回来的的数据中大部分都不可靠，这种时候我们就要考虑我们设计的问卷本身的问题，也就是它的信度低，可靠性差。

信度可分为两大类：外在信度和内在信度。

外在信度，侧重测量问卷在不同时间得到结果的稳定性程度。常用的外在信度指标为：重测信度。重测信度简单来说：一份相同的问卷，对同一批填写者，在一定的日期内，重复填写2次，如果2次填写中，每个人第一次和第二次在每个相同问题上填写的答案相近，则说明该信度较高。反之信度较差。这样做的目的，是为了减少随机误差，提高测量时的稳定性。显然，在实践中，有一定的操作成本。

内在信度，侧重问卷结构的一致性，也就是看题项是否都是考察同一个概念的问题，比如说： 当在调查学生的学习习惯是否良好时，若量表中其它问题均与学习习惯相关，但又设置了问题你平常是否喜欢吃海南鸡饭的问题，那么该量表内在信度会有所降低。

一般使用的内在信度指标为：内部一致性（克隆巴赫α系数）。在实践中，此方法被广泛应用。

$$\alpha =\frac{n}{n-1}\left(\frac{{\sigma }_t^2-{\sum }_{i=1}^n{\sigma }_i^2}{{\sigma }_t^2}\right)$$

$n$ 为测验包含的指标数

${\sigma }_t^2$ 为每个答题者的总分之间的方差

${\sigma }_i^2$ 为第 $i$ 条题目上所有答题者分数的方差

较为通俗的解释：这是一个估算：每一个题目之间协方差（刻画变化趋势是否一致）的算法，如果每个题目之间的得分不会一同变化，则很难说明：这些题目是在测量同一个概念，每个题目之间的变化趋势一致（具有同质性），则α的值会高。

—————————————————————————————— 完——————————————————————————————