【KAN】Kolmogorov-Arnold Networks (KANs)：超越传统MLP的新型神经网络架构摘要

灵犀拾荒者

于 2025-03-17 10:00:00 发布

阅读量1.1k

点赞数 26

分类专栏： KAN 资料分享文章标签：神经网络人工智能深度学习 KAN

本文链接：https://blog.csdn.net/2303_77200324/article/details/146276008

版权

KAN 同时被 2 个专栏收录

35 篇文章

订阅专栏

资料分享

17 篇文章

订阅专栏

一、摘要

受Kolmogorov-Arnold表示定理的启发，本文提出了Kolmogorov-Arnold网络（KANs）作为多层感知器（MLP）的替代方案.MLP在节点（“神经元”）上具有固定的激活函数，而KAN在边缘（“权重”）上具有可学习的激活函数。KAN根本没有线性权重--每个权重参数都被一个参数化为样条的单变量函数所取代。我们发现，这种看似简单的变化使得KAN在小规模AI +科学任务的准确性和可解释性方面优于MLP。对于精度，较小的KAN可以在函数拟合任务中实现与较大的MLP相当或更好的精度。从理论和经验上看，KAN比MLP具有更快的神经尺度律。对于可解释性，KAN可以直观地可视化，并且可以轻松地与人类用户交互。通过数学和物理学中的两个例子，KAN被证明是有用的“合作者”，帮助科学家（重新）发现数学和物理定律。总之，KAN是MLP的有前途的替代品，为进一步改进当今严重依赖MLP的深度学习模型提供了机会。

本文分享了一篇由麻省理工学院、加州理工学院等多机构合作完成的论文《Kolmogorov-Arnold Networks (KANs)》，该论文提出了一种基于Kolmogorov-Arnold表示定理的新型神经网络架构——Kolmogorov-Arnold网络（KANs），作为传统多层感知器（MLP）的替代方案。KANs通过将可学习的激活函数置于网络的边（权重）上，而非传统的节点（神经元），并以样条函数参数化替代线性权重，显著提升了模型在精度和可解释性方面的表现。论文通过理论分析和实验验证，展示了KANs在小规模AI+科学任务中优于MLP的表现，包括更快的神经扩展律和直观的可视化能力。此外，KANs在数学（结理论）和物理学（安德森局域化）中的应用表明，其可作为科学家重新发现定律的有力“合作者”。本文将详细解读论文内容，分析其创新点，并提供总结与思考。

二、论文的主要内容

1. 引言与背景

论文首先回顾了多层感知器（MLP）作为深度学习基石的地位，其基于通用逼近定理（Universal Approximation Theorem, UAT）具有强大的函数逼近能力。然而，MLP在现代架构（如Transformer）中参数量巨大且可解释性较差，成为优化瓶颈。为此，作者提出了Kolmogorov-Arnold网络（KANs），灵感来源于Kolmogorov-Arnold表示定理（公式2.1），旨在克服MLP的局限性。KANs的核心创新是将固定激活函数从节点移至边，并以可学习的样条函数替代线性权重（如图0.1所示），从而提升精度和可解释性。

2. KAN架构设计

2.1 Kolmogorov-Arnold表示定理

Kolmogorov-Arnold定理表明，任何多变量连续函数可表示为一组单变量函数的有限组合（公式2.1）。尽管该定理在数学上优雅，但其原始形式（深度2，宽度2n+1）的激活函数可能非光滑，限制了实用性。作者通过将其推广至任意深度和宽度，结合现代深度学习技术（如反向传播），赋予KANs实用价值。

2.2 KAN层定义

KAN的基本计算单元是“层”，每层由输入维度nin 和输出维度nout 定义，包含nin×nout 个单变量激活函数ϕq,p。这些函数以B样条参数化（图2.2右侧），通过残差激活形式（公式2.10）实现：

其中

在大多数情况下都是如此。spline（x）被参数化为B样条的线性组合，使得

层间计算通过简单求和完成（公式2.5），整体网络为多层组合（公式2.7）。

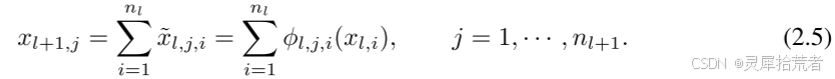
2.3 逼近能力与扩展律

作者提出了KAN的逼近理论（KAT，定理2.1），证明在光滑激活函数假设下，KAN的逼近误差随样条网格大小GGG按G^{-k-1+m}衰减（公式2.15），不受维度影响，打破维度诅咒（COD）。神经扩展律表明，测试损失随参数量N按N^{-α}下降，α=k+1，优于MLP的较慢扩展。

2.4 网格扩展技术

为提升精度，KAN引入网格扩展（图2.3右侧），通过细化样条网格，从粗粒度逐步逼近目标函数。实验表明（图2.3顶部），损失呈阶梯状下降，测试误差随GGG按理论预测缩放，训练时间随GGG线性增长（图2.3底部右侧）。

2.5 可解释性与简化技术

KAN的可解释性通过以下技术实现：

稀疏化：引入L1范数和熵正则化（公式2.18），减少冗余激活函数。

可视化：根据激活函数幅度调整透明度。
剪枝：基于节点输入输出得分（公式2.19）移除不重要神经元。

符号化：将激活函数拟合为符号形式（如sin、exp），支持用户交互。

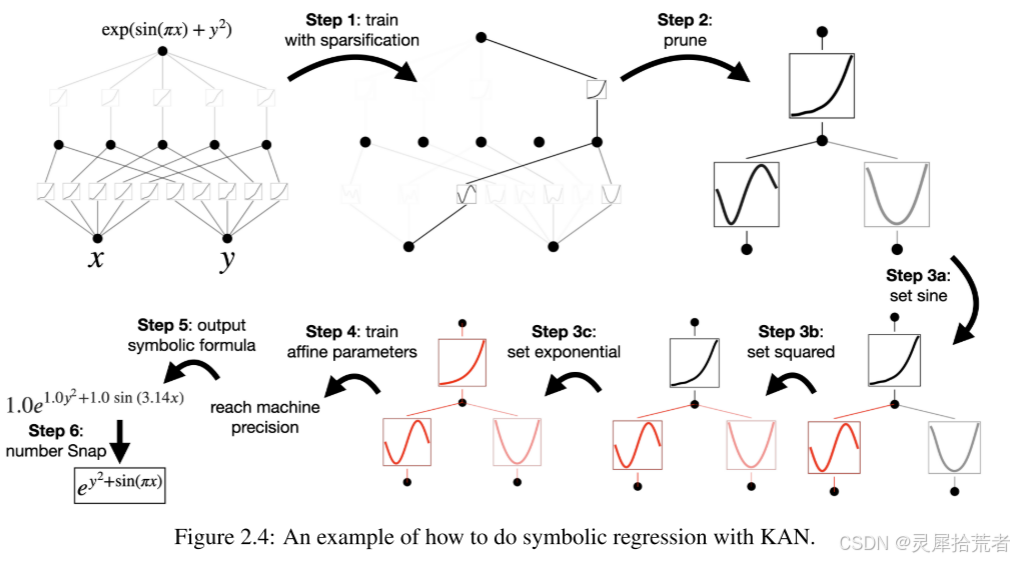
玩具实验（图2.4）展示了对f(x,y)=exp⁡(sin⁡(πx)+y2)的回归，用户通过稀疏化、剪枝和符号化逐步推导出精确公式。

3. 实验验证

3.1 数据拟合

KAN在函数拟合任务中表现出色，小型KAN即可超越大型MLP的精度，且扩展律更快（图3.1）。例如，对于高维函数，KAN有效学习其组合结构和单变量函数。

3.2 偏微分方程（PDE）求解

在泊松方程求解中，KAN替换MLP作为物理信息神经网络（PINN），显示出更高的精度和收敛速度（图3.3）。

3.3 可解释性应用

在数学（结理论）和物理学（安德森局域化）中，KAN通过可视化和符号化帮助科学家重新发现定律（图4.1），如识别特殊函数或物理规律。

4. 相关工作与讨论

论文对比了KAN与MLP、符号回归（SR）和PINN等方法，指出KAN兼具样条的局部精确性和MLP的特征学习能力。讨论中提到KAN训练速度慢（约为MLP的10倍，图6.1），但认为这是工程优化问题，而非根本限制。未来方向包括数学理论深化、算法改进及更广泛应用。

5. 代码与实现

代码开源于GitHub，支持pip安装，提供训练、剪枝、符号化等功能（表6）。

三、创新点

架构创新（图0.1、图2.2）
KAN将激活函数从节点移至边，以可学习的B样条替代线性权重，颠覆了MLP的传统设计。这种“边激活”结构结合了样条的局部精确性和MLP的全局特征学习能力，为神经网络设计提供了新范式。
理论突破（定理2.1、公式2.15）
作者推广了Kolmogorov-Arnold定理至任意深度和宽度，并提出KAT，证明KAN可打破维度诅咒，逼近误差随网格大小按G−4G^{-4}G−4衰减（对于k=3k=3k=3），优于MLP的指数级维度依赖。这一理论为神经扩展律提供了最优α=4\alpha=4α=4，刷新了对神经网络能力的认知。
精度提升（图3.1、图2.3）
KAN通过网格扩展技术（图2.3）实现动态精度提升，小型KAN即可超越大型MLP，尤其在高维函数拟合和PDE求解中（图3.3），展现了高效的参数利用率。
可解释性设计（图2.4、图4.1）
KAN引入稀疏化、剪枝和符号化技术（公式2.18-2.19），结合直观可视化，使模型不仅能拟合数据，还能揭示函数结构。玩具实验（图2.4）和科学应用（图4.1）验证了其作为“AI科学家助手”的潜力。
跨学科应用（图4.1）
KAN在数学和物理学中的成功应用（如结理论和安德森局域化）展示了其在AI+科学领域的通用性，超越了传统MLP的纯数据驱动模式。

四、总结与思考

论文提出的KANs以Kolmogorov-Arnold定理为理论基石，通过创新的边激活架构和样条参数化，显著提升了神经网络的精度和可解释性。理论上，KAN打破了维度诅咒，实现了最优神经扩展律（α=4，图2.3）；实验上，其在数据拟合（图3.1）、PDE求解（图3.3）和科学发现（图4.1）中均优于MLP。KAN的可视化与交互设计（图2.4）进一步赋予其与人类合作的潜力，使其成为AI+科学的有力工具。代码开源（表6）降低了使用门槛，为后续研究奠定了基础。

训练效率（图6.1）
KAN训练速度慢于MLP约10倍，这一瓶颈虽被归为工程问题，但若不解决，可能限制其在大规模任务中的应用。未来可探索“多头”激活分组或硬件加速。
理论局限
定理2.1假设激活函数光滑，但现实任务中函数可能非光滑或无明确KA表示，如何扩展KAN的适用性仍需研究。
应用边界
当前实验局限于小规模AI+科学任务（如图3.1、图4.1），在复杂任务（如语言建模）中的表现尚未验证。是否所有任务都存在KA表示尚存疑问。
与其他方法的融合
KAN与MLP的混合（附录B）或与Transformer的集成（如“kansformers”）可能是提升效率与通用性的方向。

总的来说，KANs为深度学习开辟了新路径，尤其在科学计算和可解释性驱动的任务中潜力巨大。建议研究者关注其算法优化与跨领域应用，以充分发挥其价值。