PINN机器学习持续火爆！Science正刊都在用！42种创新思路全面汇总

最新推荐文章于 2024-12-04 10:36:55 发布

AI科研技术派

最新推荐文章于 2024-12-04 10:36:55 发布

阅读量1k

点赞数 7

文章标签：机器学习人工智能

本文链接：https://blog.csdn.net/2401_82426425/article/details/143840845

版权

今年依然是物理信息机器学习持续爆火的一年。光是其典型代表PINN，在Science和Nature就有多篇，像模型HFM、PIGNN……近来更是迎来里程碑式突破！模型PIKANS，通过设计新的基函数，提供了一个有前途的替代方案。

主要在于，它能够利用已知的物理方程来约束机器学习模型，使模型更好地符合物理规律，提高预测准确性和可靠性。尤其在数据稀缺的情况下，能够提高数据利用效率。在金融、医疗、工程、材料学等领域，都有广泛应用。但也面临计算成本高、可解释性差、需手工选择物理知识等挑战，对它的研究成为迫切需求。

想发论文的伙伴，可以从网络设计、特征扩展、优化技术等方面入手。为方便大家研究的进行，每个方向，我都给大家提供了必读论文和源码，共42篇！

论文原文+开源代码需要的同学看文末

表示模型的修改

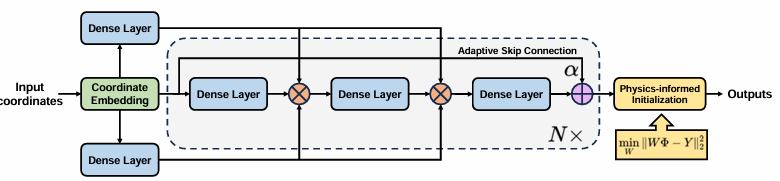
PirateNets: Physics-informed Deep Learning with Residual Adaptive Networks

内容：文章介绍了一种名为PirateNets的新型物理信息深度学习架构，旨在解决偏微分方程（PDEs）的前向和逆向问题。PirateNets通过使用自适应残差连接和独特的初始化方案，使得在训练过程中能够稳定且高效地利用深层神经网络结构，从而提高了模型的优化容易度和准确性，实现了在多个基准测试中的最先进结果。

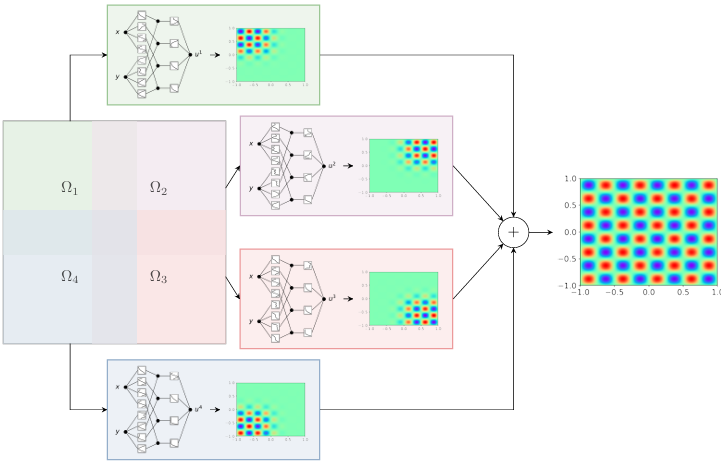
Finite basis Kolmogorov-Arnold networks: domain decomposition for data-driven and physics-informed problems

内容：文章介绍了一种基于域分解方法的Kolmogorov-Arnold网络（FBKANs），用于数据驱动和物理信息问题。FBKANs通过将多个小规模的KANs并行训练，提供了一种解决多尺度问题的准确解决方案，并且能够处理噪声数据和物理信息训练，具有比传统KANs更高的准确性和鲁棒性。

控制方程

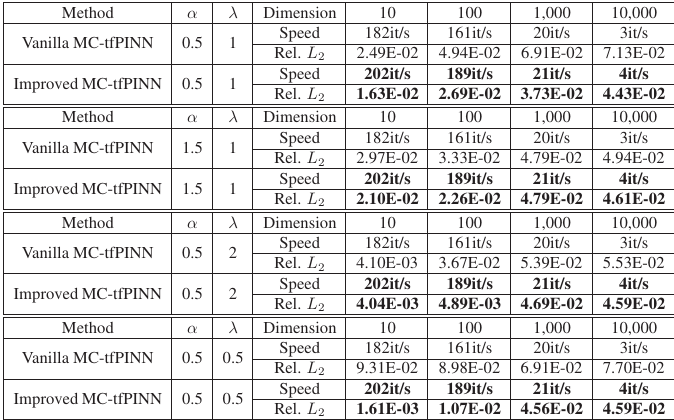
Tackling the Curse of Dimensionality in Fractional and Tempered Fractional PDEs with Physics-Informed Neural Networks

内容：文章介绍了一种基于物理信息神经网络（PINNs）的方法，用于解决高维分数阶和温度分数阶偏微分方程（PDEs），这些方程在模拟长程相互作用、异常扩散和非局部效应时非常有效。研究者们通过开发蒙特卡洛温度分数PINN（MC-tfPINN）扩展了之前工作中的蒙特卡洛分数PINN（MC-fPINN），并提出了一种改进的MC-fPINN，使用高斯求积法代替传统的蒙特卡洛方法来计算PDE算子中的一维径向奇异积分，显著减少了计算误差并提高了收敛速度。

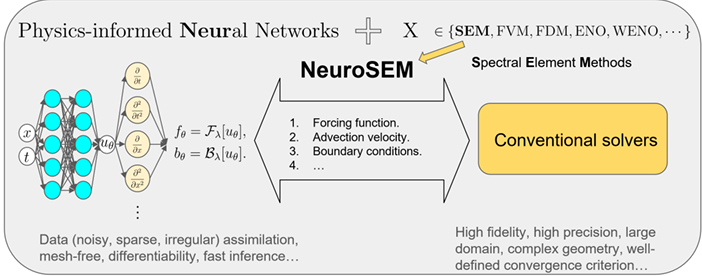
NeuroSEM: A hybrid framework for simulating multiphysics problems by coupling PINNs and spectral elements

内容：文章介绍了NeuroSEM，这是一个结合了物理信息神经网络（PINNs）和高保真谱元方法（SEM）的混合框架，用于模拟涉及流体动力学、热传递、结构力学和电磁学的多物理问题。NeuroSEM利用PINNs在特定子域中的数据同化和物理现象建模的优势，并将这些子域集成到Nektar++求解器中，以提供鲁棒的多物理问题解决方案。

优化过程

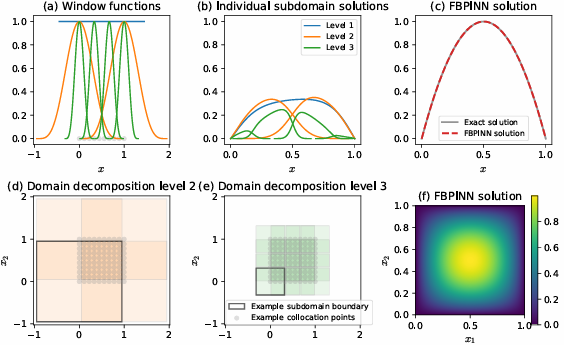
Multilevel domain decomposition based architectures for physics-informed neural networks

内容：文章提出了一种基于多级域分解的物理信息神经网络（Physics-Informed Neural Networks, PINNs）架构，用于解决涉及微分方程的多尺度问题。该方法通过将PINNs与多级域分解方法结合，显著提高了解决高频和多尺度问题的性能，并且与经典域分解方法（DDMs）类似，通过在大量子域中加入多级模型来改善全局通信，从而提高了FBPINNs的准确性。

ConFIG: Towards Conflict-free Training of Physics Informed Neural Networks

内容：文章介绍了一种名为ConFIG的新方法，旨在解决物理信息神经网络（PINNs）训练中多目标优化问题时各损失项之间的冲突。ConFIG通过确保最终更新方向与每个损失项的梯度之间保持正点积来实现无冲突更新，并动态调整梯度幅度。此外，该方法还利用动量来加速优化过程，通过交替不同损失项的反向传播来降低计算成本。