基于PyTorch的气温预测简单项目实战：从数据预处理到模型构建详解

一、项目背景与目标

在气象预测领域，利用历史数据预测未来气温是经典的时间序列分析问题。本文使用PyTorch框架，通过构建全连接神经网络模型，实现基于多特征的气温预测。项目完整展示了数据预处理、可视化分析、神经网络建模、训练优化及结果评估的全流程。

二、数据集与特征说明

2.1 数据集概览

数据集temps.csv包含以下关键字段：

• 时间特征：year（年份）、month（月）、day（日）、week（星期）

• 温度特征：temp_2（前天最高温）、temp_1（昨天最高温）、average（历史平均气温）

• 目标标签：actual（当日真实最高温）

• 特殊字段：friend（朋友猜测值）

import pandas as pd
features = pd.read_csv('temps.csv')
# 处理时间数据(转换为可以计算的统一的整体的时间格式)
import datetime

# 分别得到年，月，日
years = features['year']
months = features['month']
days = features['day']

# datetime格式
dates = [str(int(year)) + '-' + str(int(month)) + '-' + str(int(day)) for year, month, day in zip(years, months, days)]
dates = [datetime.datetime.strptime(date, '%Y-%m-%d') for date in dates]

2.2 特征可视化分析

通过Matplotlib绘制各特征趋势图，观察数据分布规律：

# 准备画图
# 指定默认风格
plt.style.use('fivethirtyeight')

# 设置布局
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(nrows=2, ncols=2, figsize = (10,10))
fig.autofmt_xdate(rotation = 45)

# 标签值
ax1.plot(dates, features['actual'])
ax1.set_xlabel(''); ax1.set_ylabel('Temperature'); ax1.set_title('Max Temp')

# 昨天
ax2.plot(dates, features['temp_1'])
ax2.set_xlabel(''); ax2.set_ylabel('Temperature'); ax2.set_title('Previous Max Temp')

# 前天
ax3.plot(dates, features['temp_2'])
ax3.set_xlabel('Date'); ax3.set_ylabel('Temperature'); ax3.set_title('Two Days Prior Max Temp')

# 我的逗逼朋友
ax4.plot(dates, features['friend'])
ax4.set_xlabel('Date'); ax4.set_ylabel('Temperature'); ax4.set_title('Friend Estimate')

plt.tight_layout(pad=2)

三、数据预处理关键技术

3.1 类别特征编码

week字段为字符串类型，使用独热编码（One-Hot Encoding）转换为数值：

 

#week列是字符串而不是数值所以要处理数据
# 独热编码
#get_dummies函数自动进行编码--方法是按照类别数量进行二进制编码，如星期一就是1000000
features = pd.get_dummies(features)

3.2 标签分离与标准化

分离标签并进行标准化处理，消除量纲影响：

# 标签（y）
labels = np.array(features['actual'])

# 在特征中去掉标签（y）
features= features.drop('actual', axis = 1)

# 名字单独保存一下，以备后患
feature_list = list(features.columns)

# 转换成合适的格式
features = np.array(features)

- 我们发现我们数值的范围是不一样的，但是神经网络的计算容易往数值大的方向去倾向（认为数值大的更重要），所以我们要归一化处理。
- 由于数据可能会是分散太开的，这样不利于进行模型分析，因此要让数据集都处于同一范围密集一点（在保留特征的完整性情况下），所以我们要减去均值，除以标准差，这样可以保证数据集的均值为0，标准差为1（正态分布化）。此时数据会变成关于原点对称分布的数据且范围得到了控制。

from sklearn import preprocessing
input_features = preprocessing.StandardScaler().fit_transform(features)

3.3 数据张量转换

将Numpy数组转换为PyTorch张量：

#转化为张量（tensor）类型
x=torch.tensor(input_features,dtype=torch.float)
y=torch.tensor(labels,dtype=torch.float)

 

四、神经网络模型构建

4.1 手动初始化参数法

定义网络参数并实现前向传播：

#权重参数初始化
# 14个输入，128个隐藏层，1个输出
weights=torch.randn((14,128),dtype=torch.float,requires_grad=True)
biases=torch.randn((128),dtype=torch.float,requires_grad=True)
weights2=torch.randn((128,1),dtype=torch.float,requires_grad=True)
biases2=torch.randn((1),dtype=torch.float,requires_grad=True)
learning_rate=0.001

之后进行编写网络结构：

learning_rate=0.001
losses=[]
for i in range(1000):
    #计算隐层，.mm()矩阵乘法方法
    hidden=x.mm(weights)+biases
    #我们每次进行第一次隐层后，都会进行一次非线性的映射
    #加入激活函数
    hidden=torch.relu(hidden)
    #预测结果
    predictions=hidden.mm(weights2)+biases2
    loss=torch.mean((predictions-y)**2)
    #转换tensor为numpy格式
    losses.append(loss.data.numpy())
    #打印损失
    if i%100==0:
        print('loss:',loss)
    #反向传播
    loss.backward()
    #更新参数
    #因为我们更新仕沿着梯度反方向更新，所以要乘-1
    weights.data.add_(- learning_rate * weights.grad.data)  
    biases.data.add_(- learning_rate * biases.grad.data)
    weights2.data.add_(- learning_rate * weights2.grad.data)
    biases2.data.add_(- learning_rate * biases2.grad.data)
    #梯度清零
    weights.grad.data.zero_()
    biases.grad.data.zero_()
    weights2.grad.data.zero_()
    biases2.grad.data.zero_()

结果：

loss: tensor(7926.9590, grad_fn=<MeanBackward0>)
loss: tensor(152.6596, grad_fn=<MeanBackward0>)
loss: tensor(144.5899, grad_fn=<MeanBackward0>)
loss: tensor(142.7679, grad_fn=<MeanBackward0>)
loss: tensor(141.9259, grad_fn=<MeanBackward0>)
loss: tensor(141.4075, grad_fn=<MeanBackward0>)
loss: tensor(141.0374, grad_fn=<MeanBackward0>)
loss: tensor(140.7513, grad_fn=<MeanBackward0>)
loss: tensor(140.5180, grad_fn=<MeanBackward0>)
loss: tensor(140.3272, grad_fn=<MeanBackward0>)

其中的Relu就是一个激活函数用于进行非线性映射方便模型适应更复杂环境：

 

 不难发现我们这样一个参数一个参数来更新、清0，一旦变量变多会很麻烦，所以pytorch里面有相应的函数来完成这些。

4.2 使用Sequential快速建模

PyTorch高阶API实现更简洁的模型定义：

input_size = input_features.shape[1]#14
hidden_size = 128
hidden2_size=256
output_size = 1
#进行一批一批来迭代，将样本进行区块化
batch_size = 16
#调用模型包
my_nn = torch.nn.Sequential(
    torch.nn.Linear(input_size, hidden_size),
    torch.nn.ReLU(),#激活函数,非线性映射一次就可以实现非线性转换
    torch.nn.Linear(hidden_size, hidden2_size),
    torch.nn.Linear(hidden2_size, output_size),
)

五、模型训练与优化

5.1 损失函数与优化器

选择均方误差损失和Adam优化器：

cost = torch.nn.MSELoss(reduction='mean')
#优化器（此处是Adam方法引入了动量、惯性概念更快找到最优解），lr是学习率
optimizer = torch.optim.Adam(my_nn.parameters(), lr = 0.001)

 此处的Adam方法是梯度下降方法，是一种高效的优化算法。该算法是在梯度下降算法(SGD)的理念上，结合Adagrad和RMSProp算法提出的，计算时基于目标函数的一阶导数，保证了相对较低的计算量。adma的优点如下：参数更新的大小不随着梯度大小的缩放而变化；更新参数时的步长的边界受限于超参的步长的设定；不需要固定的目标函数；支持稀疏梯度；它能够自然的执行一种步长的退火。

 

5.2 Mini-Batch训练

分批次训练提升效率：（特别是数据量特别多的时候）

# MINI-Batch方法来进行训练
    for start in range(0, len(input_features), batch_size):
        end = start + batch_size if start + batch_size < len(input_features) else len(input_features)
        xx = torch.tensor(input_features[start:end], dtype = torch.float, requires_grad = True)
        yy = torch.tensor(labels[start:end], dtype = torch.float, requires_grad = True)
        prediction = my_nn(xx)
        loss = cost(prediction, yy)
        optimizer.zero_grad()
        loss.backward(retain_graph=True)
        optimizer.step()
        batch_loss.append(loss.data.numpy())

完整模型代码：

# 训练网络
losses = []
for i in range(1000):
    batch_loss = []
    # MINI-Batch方法来进行训练
    for start in range(0, len(input_features), batch_size):
        end = start + batch_size if start + batch_size < len(input_features) else len(input_features)
        xx = torch.tensor(input_features[start:end], dtype = torch.float, requires_grad = True)
        yy = torch.tensor(labels[start:end], dtype = torch.float, requires_grad = True)
        prediction = my_nn(xx)
        loss = cost(prediction, yy)
        optimizer.zero_grad()
        loss.backward(retain_graph=True)
        optimizer.step()
        batch_loss.append(loss.data.numpy())
    
    # 打印损失
    if i % 100==0:
        losses.append(np.mean(batch_loss))
        print(i, np.mean(batch_loss))

训练结果：

0 3661.37
100 37.535126
200 47.15768
300 37.942654
400 42.825485
500 43.41311
600 37.980686
700 39.260796
800 41.362602
900 38.172077 

5.3 如何改善模型

简单的改动我们只需要改一下部分即可：

input_size = input_features.shape[1]#14
hidden_size = 128
hidden2_size=256
output_size = 1
#进行一批一批来迭代，将样本进行区块化
batch_size = 16
#调用模型包
my_nn = torch.nn.Sequential(
    torch.nn.Linear(input_size, hidden_size),
    torch.nn.ReLU(),#激活函数,非线性映射一次就可以实现非线性转换
    torch.nn.Linear(hidden_size, hidden2_size),
    torch.nn.Linear(hidden2_size, output_size),
)

我们可以 增加隐层（但要注意输出的维度和下一层输入维度一致），也可以改变激活函数或者改变里面的Linear模型函数，这样我们就可以得到不一样的模型。（但注意一味的增加隐层可能会导致过拟合问题）。这些留给各位自行探索！！！

六、预测结果可视化

6.1 结果数据准备

创建包含日期和预测值的DataFrame：

x = torch.tensor(input_features, dtype=torch.float)
predict = my_nn(x).data.numpy()
# 转换日期格式
dates = [str(int(year)) + '-' + str(int(month)) + '-' + str(int(day)) for year, month, day in zip(years, months, days)]
dates = [datetime.datetime.strptime(date, '%Y-%m-%d') for date in dates]

# 创建一个表格来存日期和其对应的标签数值
true_data = pd.DataFrame(data = {'date': dates, 'actual': labels})

# 同理，再创建一个来存日期和其对应的模型预测值
months = features[:, feature_list.index('month')]
days = features[:, feature_list.index('day')]
years = features[:, feature_list.index('year')]

test_dates = [str(int(year)) + '-' + str(int(month)) + '-' + str(int(day)) for year, month, day in zip(years, months, days)]

test_dates = [datetime.datetime.strptime(date, '%Y-%m-%d') for date in test_dates]

predictions_data = pd.DataFrame(data = {'date': test_dates, 'prediction': predict.reshape(-1)}) 

6.2 绘制对比曲线

直观展示预测值与真实值差异：

# 真实值
plt.plot(true_data['date'], true_data['actual'], 'b-', label = 'actual')

# 预测值
plt.plot(predictions_data['date'], predictions_data['prediction'], 'ro', label = 'prediction')
plt.xticks(rotation = 60)
plt.legend()

# 图名
plt.xlabel('Date'); plt.ylabel('Maximum Temperature (F)'); plt.title('Actual and Predicted Values');

七、关键问题解析

1. 为什么需要数据标准化？
   消除特征量纲差异，加速模型收敛

2. ReLU激活函数的作用
   引入非线性表达能力，解决梯度消失问题

3. Mini-Batch的优势
   平衡计算效率与梯度稳定性，适合大数据集

---

八、优化方向建议

1. 增加网络深度：尝试添加更多隐藏层

2. 调整超参数：优化学习率、批次大小

3. 使用LSTM：针对时序特征引入循环神经网络

4. 数据增强：加入风速、湿度等气象特征

 附录：

以下是几种常用的激活函数：

 

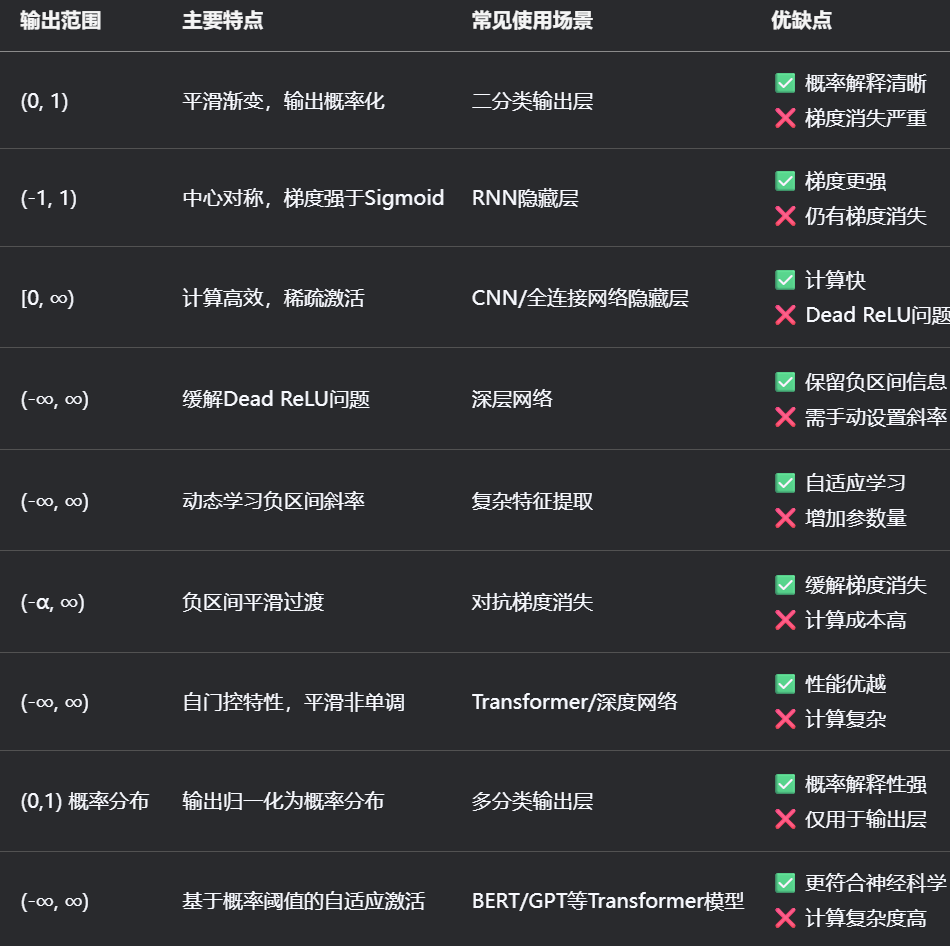
关键符号说明：

• α：可调节参数（ELU默认为1.0，PReLU可学习）

• β：Swish函数的缩放参数（通常设为1.0）

• σ：Sigmoid函数

• Φ(x)：标准正态分布累积分布函数

---

表格使用建议：

1. CNN/全连接网络首选：ReLU系列（ReLU > Leaky ReLU > PReLU）

2. RNN网络推荐：Tanh 或 Swish

3. 输出层专用：Sigmoid（二分类）、Softmax（多分类）

4. 前沿模型选择：Transformer架构优先使用GELU或Swish