劳斯判据存在全零行判断极点位置

对于线性系统，劳斯判据是重要的判断系统稳定性的工具。学习劳斯判据是为了在不求解极点具体的值的情况下快速判断系统的稳定性。

对于线性系统来讲，若极点均位于复平面的左半面时，也就是实部为负数，系统将保持稳定，若极点位于虚轴上，也就是实部为0，则系统保持临界稳定，若任一极点位于复平面的右半面，也就是实部为正数，则系统不稳定。

使用劳斯判据的第一步是写出劳斯表，举一个经典的例子。

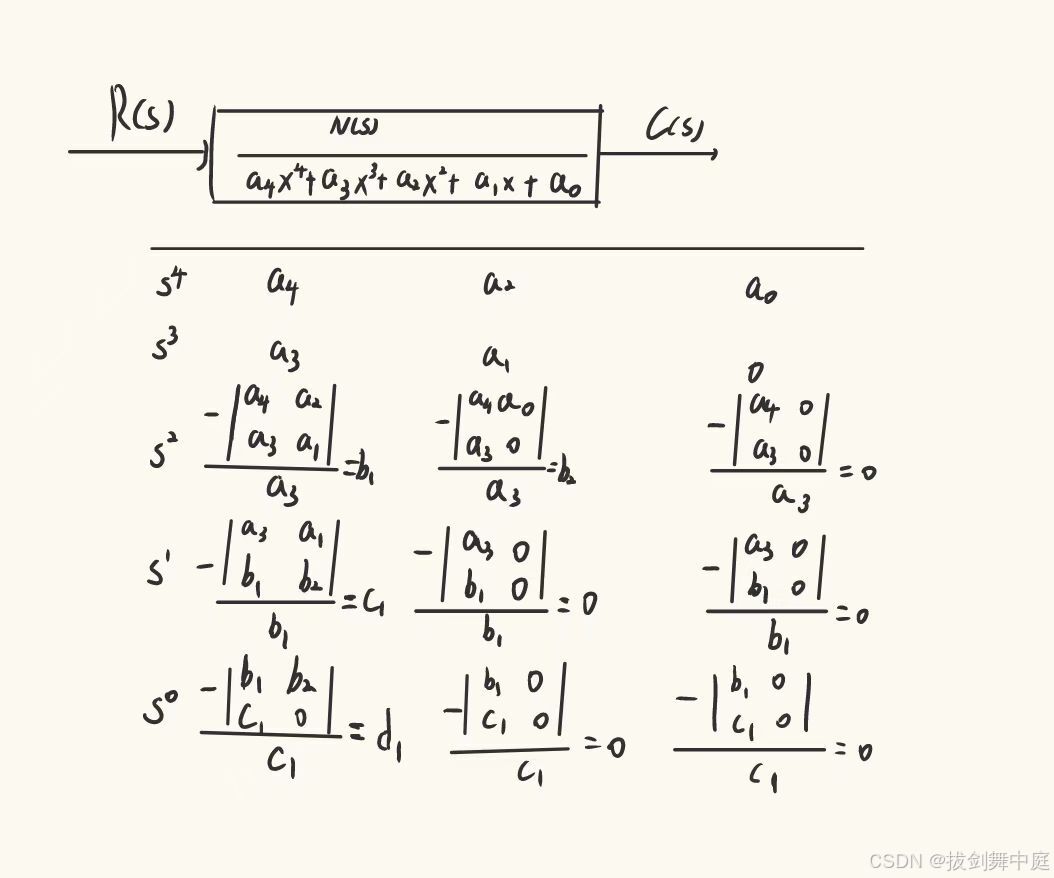
当劳斯表出现单个元素为0时，在论坛上已经有比较清晰的资料，下面着重讨论当劳斯表出现整行全为0时的情况。

对于转换函数（Transfer function)为

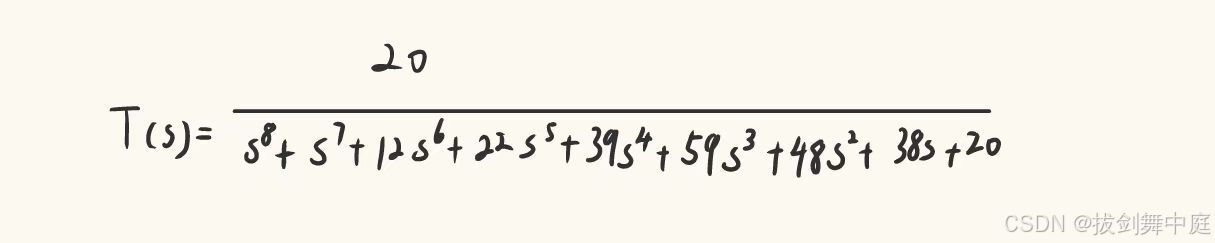
写出劳斯表，发现行出现全为0的情况，

这时，需要返回上一行，也就是行，构建辅助方程，然后将辅助方程对拉普拉斯算子求导，得出导函数，再将导函数的系数替换为该行元素，列出方程如下

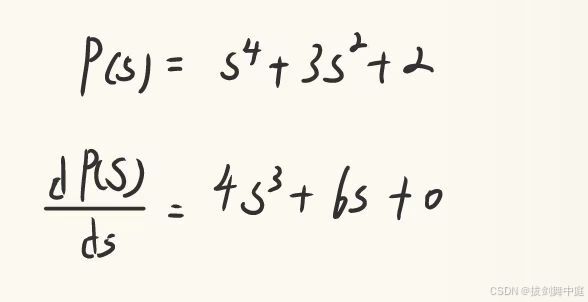
替换过后，补全劳斯表，

此时，劳斯表被分成上下两部分，上面部分按照原先原则判断，即第一列元素每变一次号，例如从3变到-1，说明有一个极点位于右半面，剩下的极点位于左半面，在本题中，变号两次，在右半面有2个极点，一共有4个极点，因此左半面有2个极点，没有位于虚轴上的极点。

对于劳斯表的下半部分，因为其行数为偶数，有对称性质，第一列每变一次号将有一个极点位于右半面，由于对称性，同时也存在一个极点位于左半面。

用总的极点个数减去已知在左右半面极点的个数，即可得到位于虚轴上的极点的个数。在本体中，下半部分第一列没有变号，意味着没有极点位于左右半面，总共有八个极点，左右半面各两个，意味着虚轴上有四个极点。