我缺的是A会吗？是撬动它的王炸思路！小波变换+KAN！创新拉满

本文链接：https://blog.csdn.net/2401_88190197/article/details/143981753

今天给大家推荐一个能发A会且不卷的思路：小波变换+KAN！

其为解决传统神经网络面临的一系列挑战（黑盒、训练速度、鲁棒性……）提供了新的视角！不仅提高了模型的性能，还增强了其可解释性！比如模型UPW便在高光谱图像分类任务中，准确率比MLP高了50.41％！

主要在于，小波变换具有多分辨率分析的能力，能够同时捕捉数据中的高频和低频特征。与KAN结合时，能够在表示复杂函数和数据模式时更加精确！且可解释性是KAN的一大亮点，而小波函数作为基函数，其特性是已知的。当它们被用于构建神经网络时，便能更容易地理解模型是如何从输入数据中提取特征的。

为了让大家能够紧跟领域前沿，找到顶会idea启发，我给大家准备了一些高分创新思路，原文和源码都有！

论文原文+开源代码需要的同学看文末

论文：Wav-KAN: Wavelet Kolmogorov-Arnold Networks

内容

该论文介绍了一种名为Wav-KAN（Wavelet Kolmogorov-Arnold Networks）的新型神经网络架构，它通过结合小波变换和Kolmogorov-Arnold网络结构来提高模型的可解释性和性能。Wav-KAN能够高效捕捉输入数据的高频和低频成分，同时保持对数据结构的准确表示并避免过拟合。

论文探讨了Wav-KAN在捕获复杂光谱空间依赖性方面的能力，并展示了将表示定理纳入深度学习模型以增强对高光谱图像等高维、相关数据性能的优势。

论文：Unveiling the Power of Wavelets: A Wavelet-based 1 Kolmogorov-Arnold Network for Hyperspectral Image Classification

内容

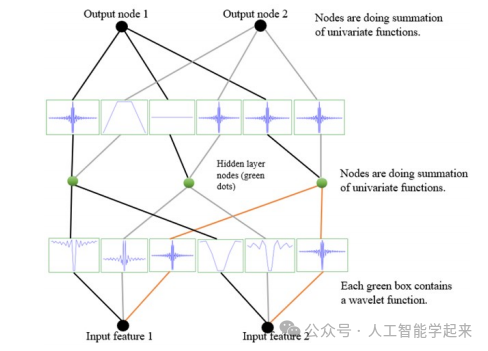
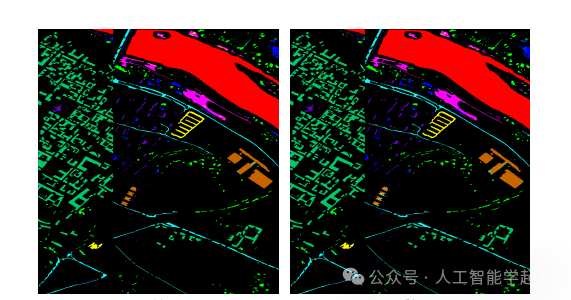
该论文介绍了一种基于小波的Kolmogorov-Arnold网络（Wav-KAN），用于高光谱图像分类。Wav-KAN利用小波函数作为可学习的激活函数，能够通过膨胀和平移有效地捕获多尺度空间和光谱模式，探讨了Wav-KAN在捕获复杂光谱空间依赖性方面的能力，并展示了将表示定理纳入深度学习模型以增强对高光谱图像等高维、相关数据性能的优势。

论文：Physics Informed Kolmogorov-Arnold Neural Networks for Dynamical Analysis via Efficent-KAN and WAV-KAN

内容

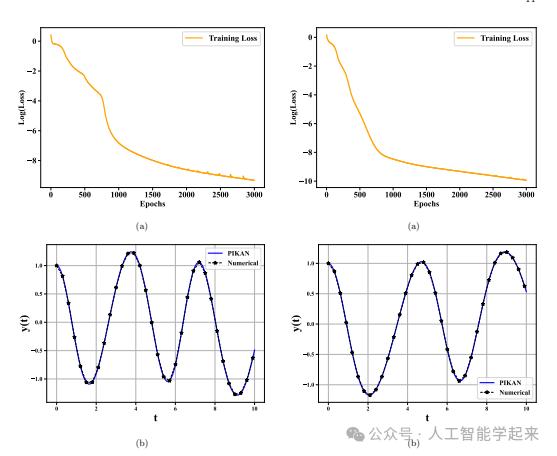
该论文介绍了一种基于物理信息的Kolmogorov-Arnold神经网络（PIKAN），通过efficient-KAN和WAV-KAN实现，用于高效解决动态分析中的微分方程问题，它利用Kolmogorov-Arnold表示定理，通过B-spline和基于小波的实现，展示了其在各种常微分方程和偏微分方程上的性能，通过无监督（无数据）和有监督（数据驱动）技术进行验证，并与数值解相比在大多数情况下达到了99%的准确率。

论文探讨了PIKAN在不同Kolmogorov-Arnold网络变体中的应用，并与物理信息神经网络（PINN）进行了比较，展示了PIKAN在架构复杂性和性能方面的优势。

论文：FC-KAN: FUNCTION COMBINATIONS IN KOLMOGOROV-ARNOLD NETWORKS

内容

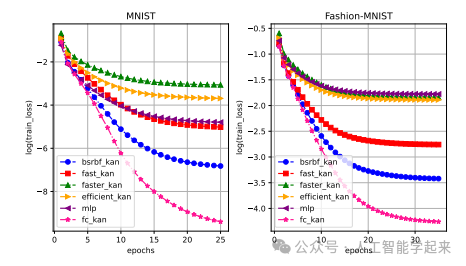
该论文介绍了FC-KAN（Function Combinations in Kolmogorov-Arnold Networks），这是一种新型的Kolmogorov-Arnold网络（KAN），它通过在低维数据上使用元素级操作（如求和、逐元素乘积等）来结合B-splines、小波和径向基函数等流行数学函数。它在MNIST和Fashion-MNIST数据集上，FC-KAN在多次独立训练运行的平均表现上超越了多层感知器（MLP）和其他现有的KAN模型。