物理信息机器学习（Physics-informed machine learning）学习笔记（1）

原文链接：Physics-informed machine learning | Nature Reviews Physics

物理信息机器学习（Physics-informed machine learning）

摘要：尽管在使用偏微分方程（partial differwntial equations, PDEs）的数值离散化模拟多物理场问题方面取得了巨大进展，但仍无法将嘈杂数据无缝整合到现有算法中，网格生成仍然复杂，且由参数化PDEs控制的高维问题无法解决。此外，解决具有隐藏物理的反问题通常成本过高，需景的替代方案出现，但训练深度神经网络需要大数据，这在科学问题中并不总是可用。相反，这些网络可以从通过强制执行物理定律（例如，在连续时空域的随机点）获得的额外信息中进行训练。这种物理信息学习整合了（嘈杂的）数据和数学模型，并通过神经网络或其他基于核的回归网络实现。此外，可能可以设计专门的网络架构，这些架构自动满足一些物理不变量，以提高准确性、加快训练速度和改善泛化能力。在这里，我们回顾了一些将物理嵌入机器学习的流行趋势，介绍了一些当前的能力和局限性，并讨论了物理信息学习在正问题和反问题（包括发现隐藏物理和解决高维问题）中的多样化应用。

关键点：

• 物理信息机器学习无缝整合数据和数学物理模型，即使在部分理解、不确定和高维的背景下。

• 基于核或神经网络的回归方法提供了有效、简单且无网格的实现。

• 物理信息神经网络在不适定（ill-posed）和反问题（inverse problems）中有效且高效，并且结合域分解可以扩展到大型问题。

• 算子回归、寻找新的内在变量和表示以及具有内置物理约束的等变神经网络架构是未来研究的有前景的领域。

• 需要开发新的框架和标准化基准以及新的数学知识，以实现可扩展、稳健和严格的下一代物理信息学习机器。

建模和预测多物理场和多尺度系统动力学仍然是一个开放的科学问题。以地球系统为例，这是一个独特的复杂系统，其动力学受到物理、化学和生物过程的相互作用的复杂控制，这些过程在跨越17个数量级的空间和时间尺度上发生。在过去的50年中，通过使用有限差分（finite differences）、有限元（finite elements）、谱（spectral）方法甚至无网格（meshless）方法等，数值求解偏微分方程（PDEs），在从地球物理学到生物物理等不同应用中理解多尺度物理方面取得了巨大进展。尽管取得了不懈的进展，但使用经典分析或计算工具建模和预测具有非均匀尺度级联（inhomogeneous cascades-of-scales）的非线性多尺度系统的演变不可避免地面临严峻挑战，并引入了高昂的成本和多种不确定性来源。此外，解决反问题（例如推断功能材料中的材料属性或发现反应传输中缺失的物理）通常成本过高，需要复杂的公式、新算法和精细的计算机代码。最重要的是，通过传统方法解决具有缺失、不完整或嘈杂边界条件的实际物理问题是目前不可能的。

这就是观测数据发挥关键作用的地方。随着未来十年内超过一万亿个传感器的前景，包括空中、海上和卫星遥感，大量多保真度观测数据已准备好通过数据驱动方法进行探索。然而，尽管可用（收集或生成）的数据流的数量、周转和种类繁多，但在许多实际情况下，仍然不可能将这些多保真度数据无缝整合到现有物理模型中。数学（和实践）数据同化工作已经蓬勃发展；然而，可用数据的丰富性和时空异质性，以及缺乏普遍接受的模型，突显了需要一种变革性方法。这就是机器学习（ML）发挥作用的地方。它可以探索巨大的设计空间，识别多维相关性，并管理不适定问题。例如，它可以帮助检测气候极端事件或统计预测动态变量，如降水或植被生产力。深度学习方法特别自然地提供了从目前可用的大量多保真度并且具有前所未有的空间和时间覆盖范围的观测数据中自动提取特征的工具。它们还可以帮助将这些特征与现有近似模型联系起来，并利用它们构建新的预测工具。即使对于生物物理和生物医学建模，这种机器学习工具与多尺度和多物理场模型之间的协同整合也最近被倡导。

在科学领域，一个共同的当前主题是收集和创建观测数据的能力远远超过了合理同化这些数据的能力，更不用说理解它们了（框1）。尽管它们具有巨大的经验承诺和一些初步的成功，但大多数ML方法目前无法从这些数据洪流中提取可解释的信息和知识。此外，纯粹的数据驱动模型可能非常适合观测数据，但由于外推或观测偏差，预测可能在物理上不一致或不可信，这可能导致泛化性能不佳。因此，迫切需要通过“教”ML模型关于控制物理规则来整合基本物理定律和领域知识，这反过来可以提供“先验信息”——也就是说，在观测约束之上提供强大的理论约束（theoretical constraints）和归纳偏差（inductive biases）。为此，物理信息学习被定义为这样一个过程：通过我们对世界的观测、经验、物理或数学理解所获得的先验知识可以被利用来提高学习算法的性能。最近反映这种新的学习理念的一个例子是“物理信息神经网络”（PINNs）家族。这是一类深度学习算法，能够无缝整合数据和抽象数学算子，包括有或没有缺失物理的PDEs（框2,3）。开发这些算法的主要动机是，这种先验知识或约束可以产生更具可解释性的ML方法，这些方法在不完美数据（如缺失或嘈杂值、异常值等）存在时仍然稳健，并且可以提供准确且物理上一致的预测，即使对于外推/泛化任务也是如此。

框1：数据和物理情景

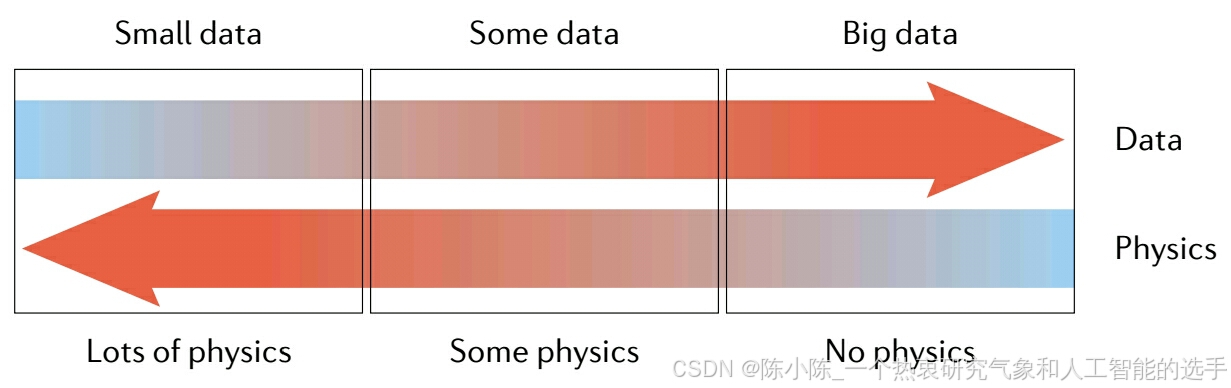
下面的图表示意性地说明了物理问题和相关可用数据的三个可能类别。在小数据体制中，假设人们知道所有的物理知识，数据提供用于初始和边界条件以及偏微分方程的系数。在应用中普遍存在的体系是中间的，其中人们知道一些数据和一些物理知识，可能缺少一些参数值，甚至偏微分方程中的整个项，例如，对流 - 扩散 - 反应系统中的反应。最后，在大数据体系中，人们可能不知道任何物理知识，数据驱动的方法可能最有效，例如，使用算子回归方法（operator regression methods）来发现新的物理知识。物理信息机器学习可以以统一的方式无缝整合数据和控制物理定律，包括具有部分缺失物理的模型。这可以使用自动微分和设计尊重底层物理原理的产生预测的神经网络简洁地表达。

框2 |：物理信息学习的原则

使学习算法具有物理信息性，意味着引入适当的观测偏差、归纳偏差或学习偏差，这些偏差可以引导学习过程识别出物理上一致的解决方案（见图）。具体如下：

• 观测偏差 可以通过体现底层物理的数据或精心设计的数据增强程序直接引入。在这样的数据上训练机器学习（ML）系统，使其能够学习反映数据物理结构的函数、向量场和算子。

• 归纳偏差 对应于可以专门纳入 ML 模型架构的先验假设，以确保所寻求的预测隐含地满足一组给定的物理定律，通常以某些数学约束的形式表达。可以说，这是使学习算法具有物理信息性的最合理方式，因为它允许底层物理约束被严格满足。然而，这种方法通常限于考虑相对简单的对称群（如平移translations、排列permutations、反射reflections、旋转rotations等）且已知先验，且可能导致复杂的实现难以扩展。

• 学习偏差 可以通过适当选择损失函数（loss functions）、约束和推理算法来引入，这些可以调节 ML 模型的训练阶段，明确支持收敛到符合底层物理的解决方案。通过使用和调整这些软惩罚约束（soft penalty constraints），底层物理定律只能近似满足；然而，这提供了一个非常灵活的平台，用于引入可以表达为积分、微分甚至分数方程的广泛物理偏差。

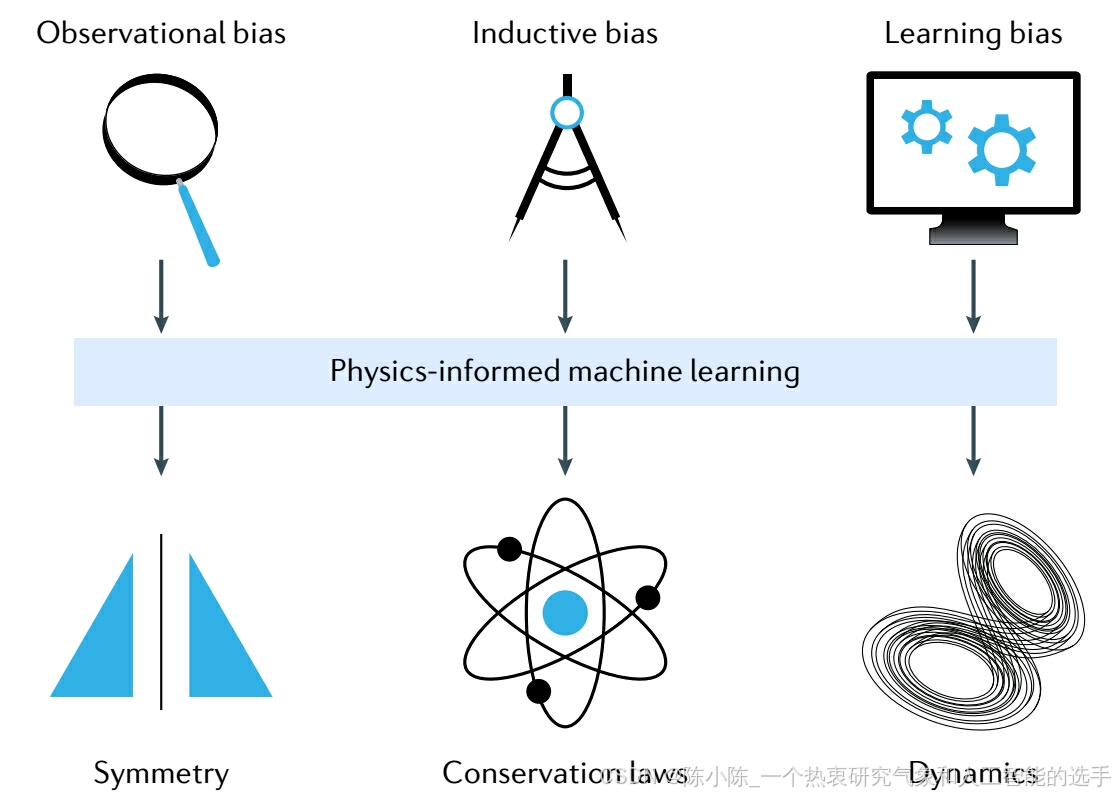
这些不同模式的偏差引导学习算法找到物理上一致的解决方案并非相互排斥，可以有效结合，产生一系列混合方法，用于构建物理信息学习机器。

框3：物理信息神经网络

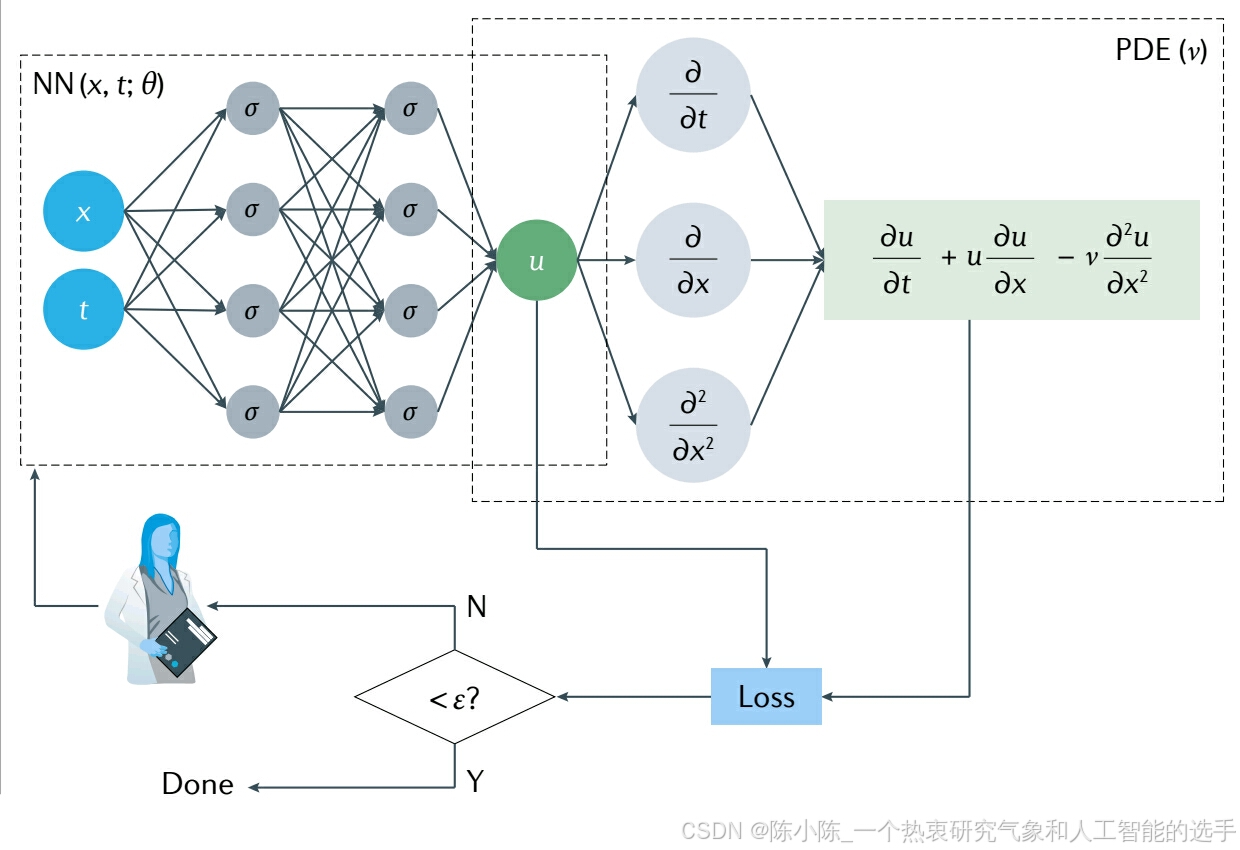
物理信息神经网络（Physics-informed nerual networks, PINNs）通过使用自动微分将 PDEs 嵌入神经网络的损失函数中，无缝整合来自测量和偏微分方程PDEs 的信息。PDEs 可以是整数阶 PDEs、积分 - 微分方程、分数PDEs 或随机 PDEs。

这里，我们以粘性 Burgers 方程为例，介绍 PINN 算法解决正问题的方法：

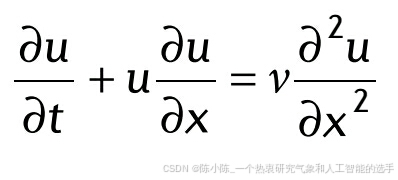
带有合适的初始条件和Dirichlet边界条件。在图中，左侧（无物理信息）网络代表 PDE 解 u(x, t) 的代理，而右侧（物理信息）网络描述 PDE 残差：

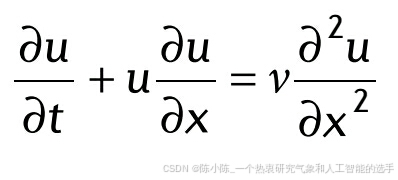
损失函数包括来自初始和边界条件的数据测量的 u 的监督损失和 PDE 的无监督损失：

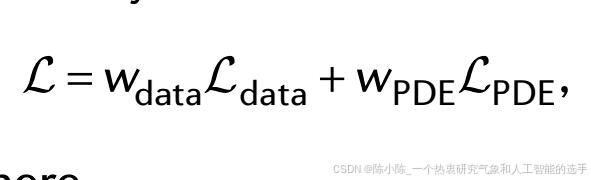
其中，

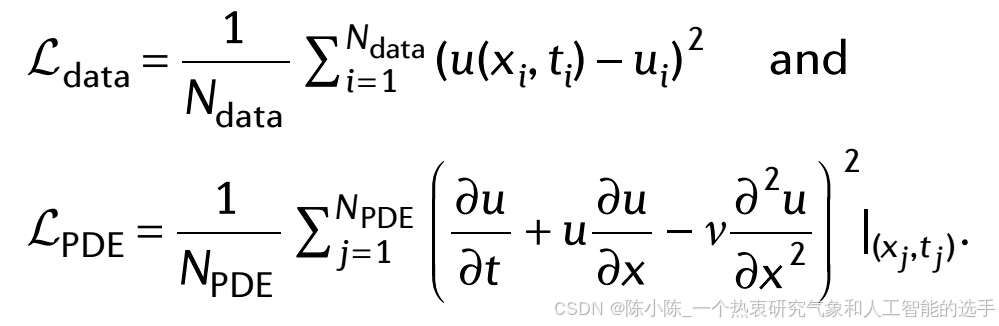
尽管存在许多公共数据库，但用于复杂物理系统的有用实验数据量是有限的。这种系统预测建模的具体数据驱动方法关键取决于可用数据量和系统本身的复杂性，如框1所示。经典范式显示在框1图的左侧，假设唯一可用的数据是边界条件和初始条件，而特定的控制PDEs及其相关参数是精确已知的。在另一个极端（框1图的右侧），可能有很多数据可用，例如以时间序列的形式，但控制物理定律（底层PDE）在连续层面可能未知。对于大多数实际应用，最有趣的类别在图的中心描绘，假设物理部分已知（即，守恒定律，但不是基本关系），但有几个分散的测量（主要或辅助状态）可用于推断PDE中的参数，甚至缺失的函数项，同时恢复解决方案。很明显，这个中间类别是最普遍的情况，并且实际上它代表了其他两个类别，如果测量太少或太多。这种“混合”情况可能导致更复杂的情景，其中PDEs的解是一个随机过程，由于随机激发或不确定的材料属性。因此，随机PDEs可以用来表示这些随机解和不确定性。最后，有许多涉及长期时空相互作用的问题，如湍流、粘弹性塑性材料或其他异常传输过程，其中非局部或分数阶微积分和分数阶PDEs可能是充分描述这些现象的适当数学语言，因为它们表现出丰富的表达性，这与深度神经网络（DNNs）的表达性不相上下。

在过去二十年中，为了在计算机模拟中考虑不确定性量化所做的努力导致了高度参数化的公式，这可能包括数百个不确定参数用于复杂问题，通常使这些计算在实践中不可行。通常，国家实验室的计算机代码甚至开源程序，如OpenFOAM或LAMMPS，都有超过100,000行代码，这使得几乎不可能维护和迭代更新它们。我们相信，可以使用物理信息学习克服这些基本和实际问题，无缝整合数据和数学模型，并使用PINNs或其他基于非线性回归的物理信息网络（PINs）（框2）实现它们。

在这篇综述中，我们首先描述了如何将物理嵌入到机器学习中，以及不同的物理如何为开发新的神经网络（NN）架构提供指导。然后，我们介绍了一些物理信息学习机器的新功能，并强调了相关的应用。这是一个快速发展的领域，因此在最后，我们提供了一个展望，包括对当前局限性的一些思考。还可以在参考文献12中找到与ML整合的几种现有基于物理的方法的分类。

如何将物理嵌入 ML

无法在没有假设的情况下构建预测模型，因此，如果没有适当的偏差，ML 模型无法预期泛化性能。具体到物理信息学习，目前有三种途径可以单独或同时遵循，通过将物理嵌入其中来加速 ML 模型的训练并增强其泛化能力（框 2）。

观测偏差（observational biases）

观测数据也许是 ML 最近成功的基石。它们也是概念上将偏差引入 ML 的最简单方式。给定足够的数据覆盖学习任务的输入域，ML 方法在实现准确插值方面表现出惊人的能力，即使对于高维任务也是如此。对于物理系统而言，得益于传感器网络的快速发展，现在可以利用大量不同保真度的观测数据，并在多个空间和时间尺度上监测复杂现象的演变。这些观测数据应该反映生成它们的底层物理原理，原则上，可以作为将这些原理嵌入 ML 模型的弱机制，在其训练阶段。例如，参见参考文献 13-16 中提出的神经网络。然而，特别是对于过度参数化的深度学习模型，通常需要大量数据来加强这些偏差并生成尊重某些对称性和守恒定律的预测。在这种情况下，一个直接的困难与数据获取成本有关，对于物理和工程科学中的许多应用，这可能非常大，因为观测数据可能通过昂贵的实验或大规模计算模型生成。

归纳偏差（inductive biases）

另一种观点关注于设计专门的神经网络（NN）架构，这些架构隐含地嵌入与给定预测任务相关的任何先验知识和归纳偏差。毫无疑问，这一类中最著名的例子是卷积神经网络（convolutional NNs），它们通过巧妙地遵守自然图像中发现的对称性群的不变性和分布式模式表示，彻底改变了计算机视觉领域。其他代表性示例包括图神经网络（graph NN, GNNs）、等变网络（equivariant networks）、核方法（kernel methods）如高斯过程，以及更一般的 PINs，其核心是直接引入由控制给定任务的物理原理。卷积网络可以推广以尊重更多的对称性群，包括旋转、反射和更一般的规范对称性变换。这使得开发一类非常通用的 NN 架构成为可能，这些架构仅依赖于内在几何形状，为涉及医学图像、气候模式分割等的计算机视觉任务提供了非常有效的模型。也可以通过基于小波（wavelet）的散射变换构建平移不变表示，这些变换对变形稳定并保留高频信息。另一个示例包括协变神经网络（covariant NNs），专门设计以符合多体（many-body）系统中存在的旋转和平移不变性（图 1a）。类似示例是等变变换器网络（equivariant transformer networks），这是一类可微映射，提高了模型对预定义连续变换群的鲁棒性。尽管它们非常有效，但这些方法目前仅限于具有相对简单和明确定义的物理或对称性群的任务，并且通常需要工艺和复杂的实现。此外，将它们扩展到更复杂任务是具有挑战性的，因为许多物理系统所具有的底层不变性或守恒定律通常理解不足或难以隐含地编码到神经架构中。

广义卷积不是设计具有强隐含偏差架构的唯一组成部分。例如，通过使用矩阵值函数（matrix-valued function）的行列式，可以在NNs中获得输入变量交换下的反对称性（anti-symmetry）。参考文献 33 提出将基于键序的物理模型与 NN 结合，并将结构参数分为局部和全局部分，以预测大规模原子建模中的原子间势能面。在另一项工作34中，使用不变张量（invariant tensor）基将伽利略不变性（Galilean invariance）嵌入到网络架构中，这显著提高了 NN 在湍流建模中的预测精度。对于识别哈密顿（Hamiltonian）系统的问题，设计网络以保持底层哈密顿系统的辛结构（symplectic structure）。例如，参考文献 36 修改了自编码器（auto-encoder）以表示 Koopman 算子，用于识别将非线性动力学重新表述为近似线性动力学的坐标变换。

具体到使用 NNs 解决微分方程，可以修改架构以精确满足所需的初始条件、狄利克雷边界条件、诺伊曼边界条件、罗宾边界条件、周期边界条件和交界面条件。此外，如果事先知道 PDE解的一些特征，也可以将它们编码到网络架构中，例如，多尺度特征、偶/奇对称性和能量守恒、高频等。

对于一个具体示例，我们参考最近在参考文献 48 中的工作，提出了 NN 架构与某些哈密顿 - 雅可比偏微分方程（Hamilton-Jacobi PDEs, HJ-PDEs）的粘性解之间的新联系。图 1b 中的两层架构定义如下

这是著名的Lax-Oleinik公式。这里， x 和 t 是空间和时间变量， L 是一个凸的且具有 Lipschitz 连续性的激活函数， a_i \in \mathbb{R} 和 u_i \in \mathbb{R}^n 是 NN 参数， m 是神经元的数量。参考文献 48 显示 f 是以下 HJ-PDE 的粘性解

其中，Hamiltonian H 和初始数据 J 明确由参数和激活函数 L 给出。Hamiltonian H必须是凸的，但初始数据J不是。参考文献 48 的结果不依赖于为 NNs 建立的通用近似定理。相反，参考文献 48 中的NNs显示 HJ-PDEs 的某些类别中包含的物理可以自然地由特定的 NNs 架构编码，而无需在高维中进行数值近似。

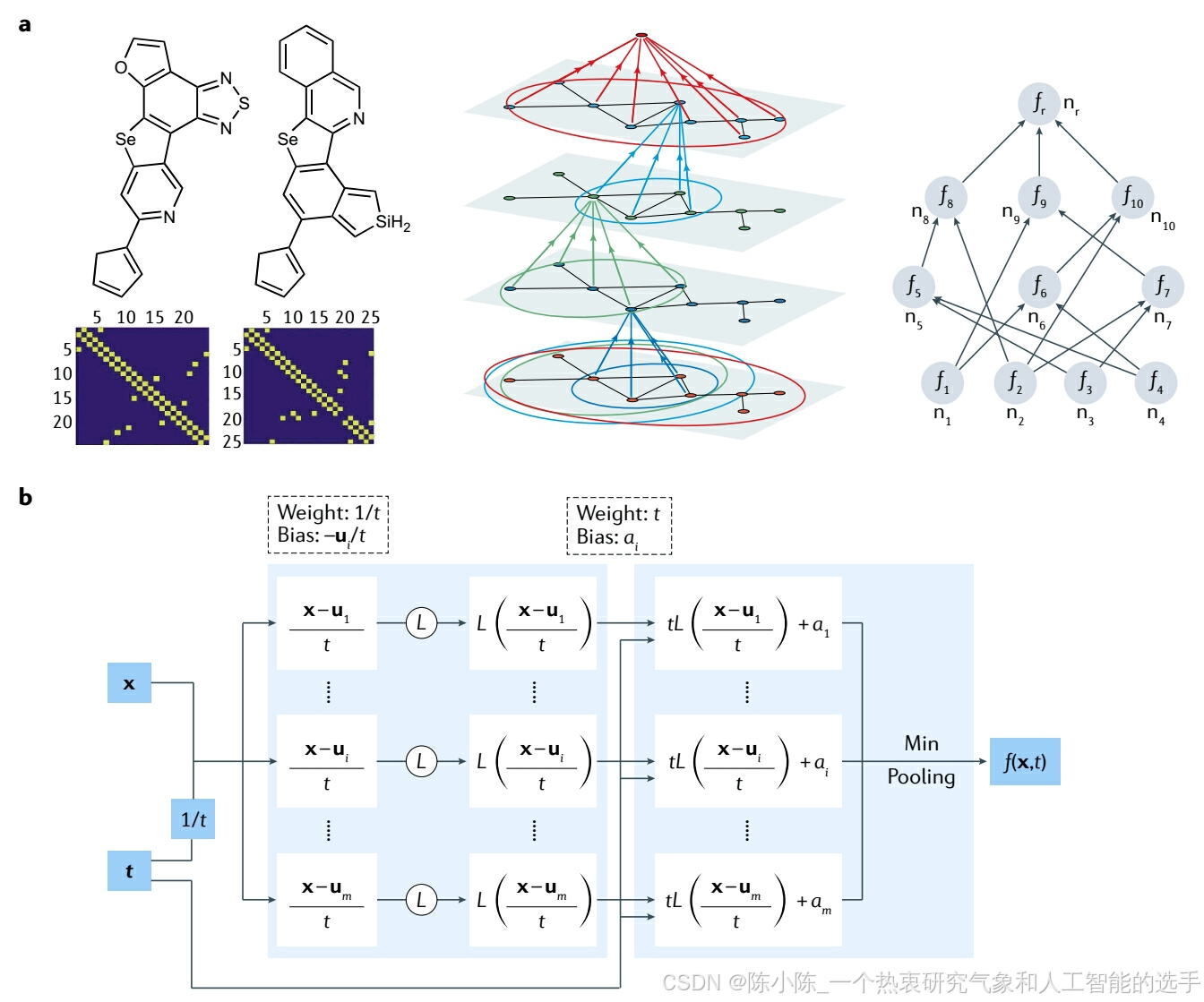
图1：物理信息神经网络结果。a：用协变组成网络（covariant compositional networks）预测分子性质。该架构基于图神经网络，并通过分解成子图的层次结构（中）和形成一个神经网络来构建，其中每个“神经元”对应于一个子图，并从对应于较小子图的其他神经元接收输入（右）。中间的面板显示了如何等效地将其视为一种算法，其中每个顶点接收并聚合来自其邻居的消息。左边给出的是从哈佛清洁能源（HCEP）数据集得到的C18H9N3OSSe和C22H15NSeSi分子图以及相对于的邻接矩阵（adjacency matrices）。b：用Lax-Oleinik公式表示的神经网络体系结构。f是Hamilton-Jacobi偏微分方程的解，x和t是空间和时间变量，L是一个凸Lipschitz激活函数，ai和ui是神经网络的参数，m是神经元数量。