动手学运动规划:2.3.c 贝塞尔曲线代码解析

That’s my spot! — 生活大爆炸 谢耳朵

🏰代码及环境配置：请参考 环境配置和代码运行!

---

本节提供了贝塞尔曲线的代码测试

python3 tests/curves/bezier_path.py

2.3.c.1 3次样条曲线代码实现

在bezier函数, 我们实现了上一节贝塞尔曲线的一般性定义公式. bernstein_poly 函数就是公式中$binomialterm$和$polynomialterm$的乘积. $binomialterm$公式我们调用了scipy.special.comb 接口.

输入一组控制点control_points 和t. 该函数返回t 处的贝塞尔曲线点.

def bezier(t, control_points):
    n = len(control_points) - 1
    return np.sum(
        [bernstein_poly(n, i, t) * control_points[i] for i in range(n + 1)], axis=0
    )
    
def bernstein_poly(n, i, t):
    return scipy.special.comb(n, i) * t**i * (1 - t) ** (n - i)    

在calc_bezier_path中, 从1到1了采样t, 循环调用bezier函数生成了完整的贝塞尔曲线

def calc_bezier_path(control_points, n_points=100):
    traj = []
    for t in np.linspace(0, 1, n_points):
        traj.append(bezier(t, control_points))

    return np.array(traj)

2.3.c.2 3次样条曲线代码测试

我们提供两组贝塞尔曲线测试:main(). 效果如下:

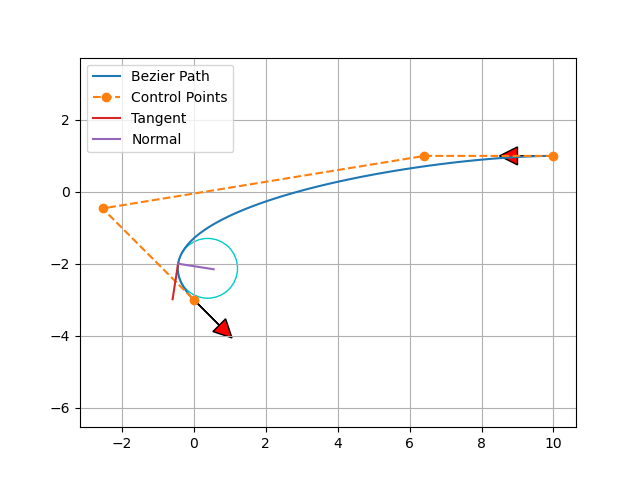
在$t=0.86$的贝塞尔曲线点上, 我们将贝塞尔曲线的1阶和2阶信息通过切向(Tangent),法向(Normal)和曲率圆画了出来. 这里利用了一个特性: Bezier曲线的导数也是一个Bezier曲线，并且控制点就是原始曲线控制点的导数。

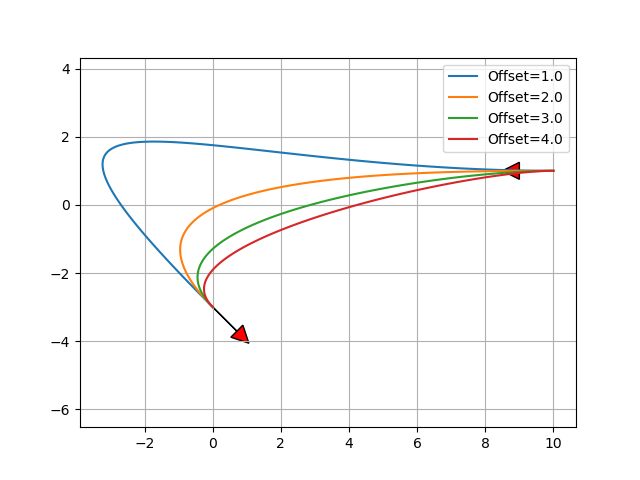
main2() 展示了始末点相同, 中间控制点不同生成的贝塞尔曲线的不同:

---

🏎️自动驾驶小白说官网：https://www.helloxiaobai.cn

🐮GitHub代码仓：https://github.com/Hello-Xiao-Bai/Planning-XiaoBai!

🔥课程答疑,面试辅导:https://shop380995420.taobao.com

🌠代码配合官网教程食用更佳！

🚀知乎，微信，知识星球全平台同号！