你见过凌晨三点的洛杉矶吗 —科比 布莱恩特
🏰代码及环境配置：请参考0.2 环境配置和代码运行 | 动手学运动规划!
1.2.1 阿克曼转向模型(Ackermann steering geometry)
阿克曼转向模型是一种为了解决交通工具转弯时，内外转向轮路径指向的圆心不同的几何学，
这个想法是由德国车辆工程师“Lankensperger”于1817年提出的，之后由他的英国代理商Rudolph Ackermann于1818年提出专利。
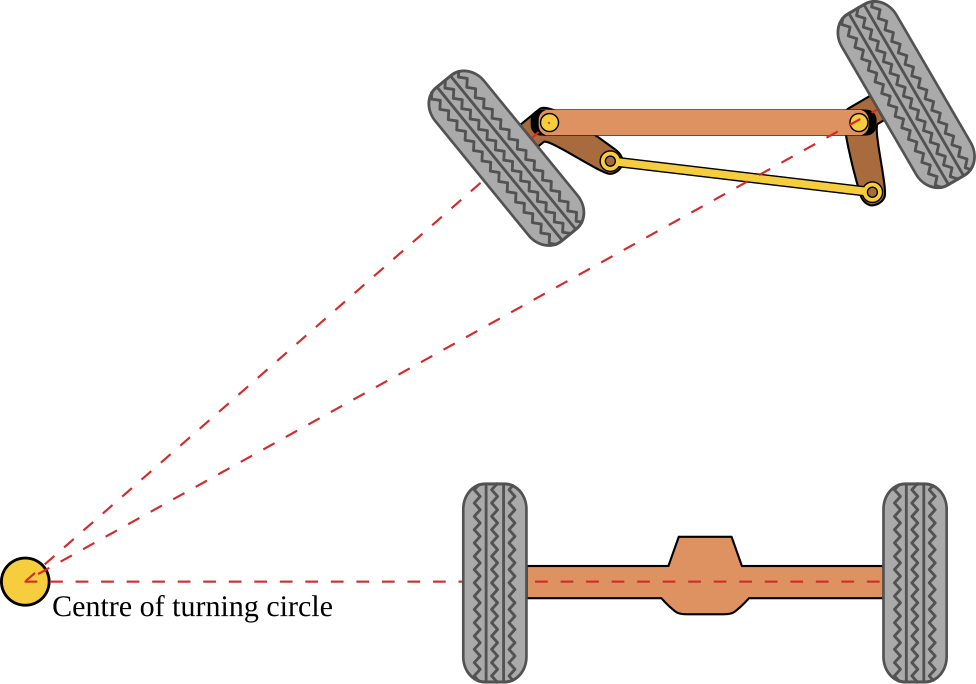
依据阿克曼转向几何设计的车辆在转弯时，两个前轮是转向角不一样.内侧轮比外侧轮的转向角大;两个后轮不转向;四个轮子路径的圆心会交汇到同一个点,也就是瞬时转向中心.
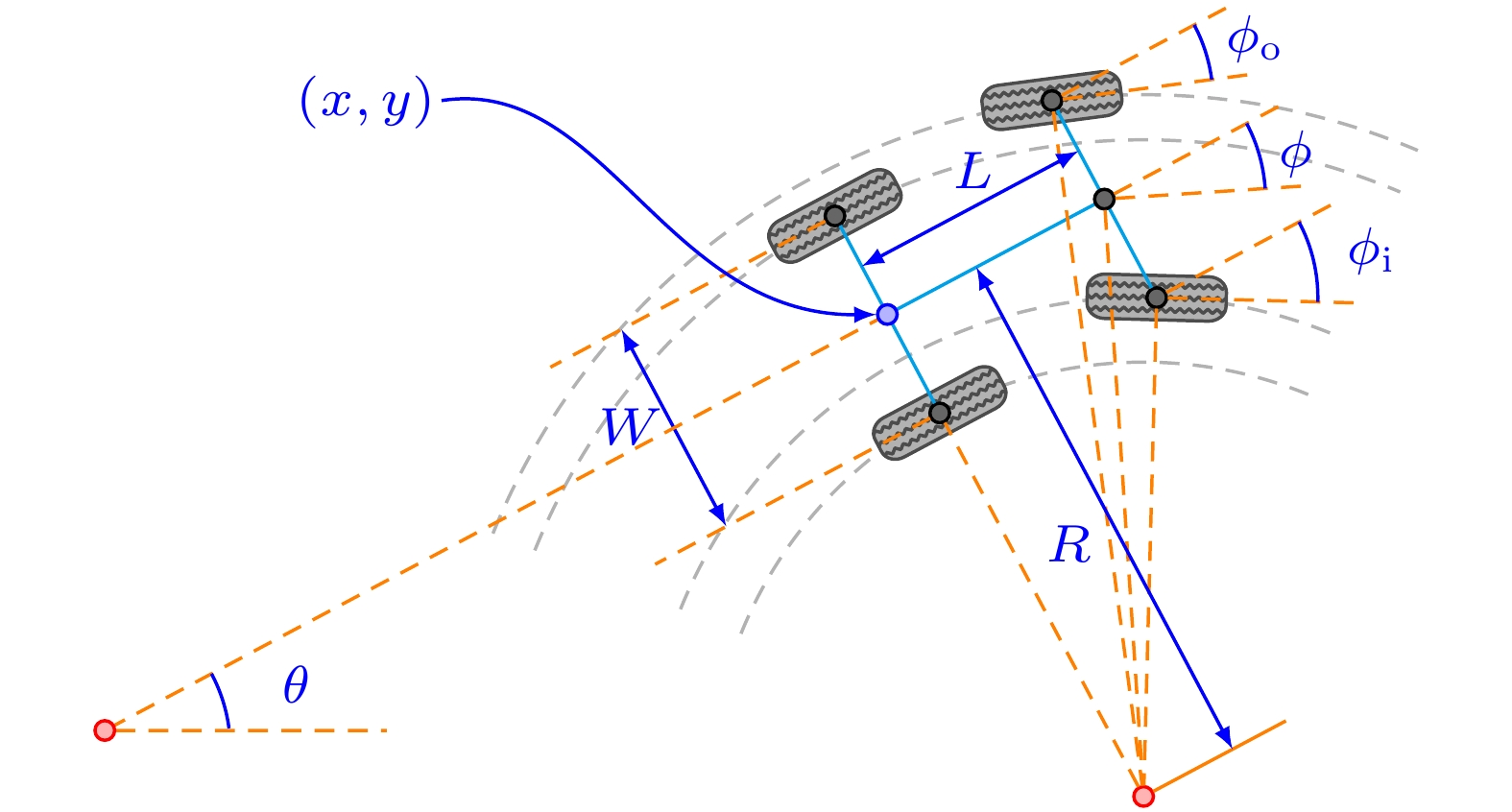
(1) 基本参数
- v : v: v:车辆速度。
- ( X , Y ) : (X,Y): (X,Y):车辆后轴中心位置.
- O : O: O:车辆瞬时转向中心.
- R : R: R:车辆瞬时转向半径.
- θ : \theta: θ:航向角,车辆当前位置与横坐标的夹角，即车辆的行驶方向。
- ω : \omega: ω:车辆绕瞬时转向中心旋转的角速度。
- δ i , δ o : \delta_i,\delta_o: δi,δo:内侧前轮转角,外侧前轮转角。
- L : L: L:轴距,前后轮之间的距离。
- W : W: W:车辆宽度
- Δ t \Delta t Δt:时间步长
(2) 前轮偏角的几何关系
由于阿克曼模型的两前轮转角不同,可以分别得到
内侧前轮转角,外侧前轮转角,平均前轮转角:
t a n ( δ o ) = L R + W 2 t a n ( δ i ) = L R − W 2 t a n ( δ ) = δ o + δ i 2 ≅ L R \begin{aligned}tan(\delta_o) &=\frac{L}{R+\frac{W}{2}} \\ tan(\delta_i) & =\frac{L}{R-\frac{W}{2}}\\ tan(\delta) &= \frac{\delta_o+\delta_i}{2} \\ &\cong \frac{L}{R}\end{aligned} tan(δo)tan(δi)tan(δ)=R+</
最低0.47元/天 解锁文章
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
