NLP学习路线图（二）： 概率论与统计学（贝叶斯定理、概率分布等）

引言

自然语言处理（NLP）作为人工智能的重要分支，致力于让机器理解、生成和操作人类语言。无论是机器翻译、情感分析还是聊天机器人，其底层逻辑都离不开数学工具的支持。概率论与统计学是NLP的核心数学基础之一，它们为语言模型、文本分类、信息检索等任务提供了理论框架。本文将深入探讨概率论与统计学在NLP中的应用，重点解析贝叶斯定理、概率分布及其实际案例。

一、概率论基础

1. 概率的基本概念

概率是描述随机事件发生可能性的度量。在NLP中，语言的模糊性和多样性使得概率模型成为处理不确定性问题的关键工具。例如：

• 词频概率：单词在语料库中出现的频率。

• 句子生成概率：某个句子符合语法和语义规则的可能性。

概率与频率的区别

• 频率学派：概率是长期重复实验中事件发生的频率。

• 贝叶斯学派：概率是对事件发生的主观信念，可随新证据更新。

2. 条件概率与联合概率

• 条件概率（Conditional Probability）：事件A在事件B已发生条件下的概率，记为 P(A∣B)P(A∣B)。
  公式：

 

• NLP应用：在文本分类中，计算某类文档中出现特定词的概率。

• 联合概率（Joint Probability）：多个事件同时发生的概率，记为 P(A,B)P(A,B)。
  NLP应用：语言模型中计算多个单词连续出现的概率（如n-gram模型）。

3. 边缘概率与独立性

• 边缘概率（Marginal Probability）：通过联合概率对其他变量求和/积分得到单个事件的概率。
  例如：P(A)=∑BP(A,B)P(A)=∑B​P(A,B)。

• 独立性：若 P(A,B)=P(A)P(B)P(A,B)=P(A)P(B)，则事件A和B独立。
  NLP应用：朴素贝叶斯分类器假设特征（单词）之间相互独立。

二、贝叶斯定理：NLP的基石

1. 贝叶斯定理的公式与推导

贝叶斯定理将条件概率与先验知识结合，用于更新事件概率。其公式为：

其中：

• P(A∣B)P(A∣B)：后验概率（Posterior）

• P(B∣A)P(B∣A)：似然概率（Likelihood）

• P(A)P(A)：先验概率（Prior）

• P(B)P(B)：证据（Evidence）

2. 贝叶斯定理在NLP中的应用

案例：垃圾邮件分类

假设需要判断一封邮件是否为垃圾邮件（事件S），邮件中包含单词“免费”（事件F）。根据贝叶斯定理：

 

• P(S)：训练集中垃圾邮件的比例（先验）。

• P(F∣S)：垃圾邮件中出现“免费”的概率（似然）。

• P(F)：所有邮件中出现“免费”的总概率。

通过计算后验概率 P(S∣F)，可决定是否将邮件标记为垃圾邮件。

扩展：朴素贝叶斯分类器

朴素贝叶斯假设所有特征（单词）条件独立，简化计算：

 尽管独立性假设在现实中不成立（例如“信用卡”和“密码”常共现），但朴素贝叶斯在文本分类中仍表现优异。

三、概率分布与NLP

1. 离散型概率分布

（1）二项分布（Binomial Distribution）

描述n次独立试验中成功次数的概率分布。
概率质量函数（PMF）：

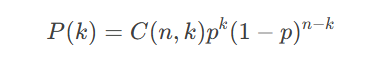
NLP应用：模拟文本中二元事件（如某个词是否出现）。

（2）多项分布（Multinomial Distribution）

二项分布的扩展，描述多类别试验的结果。
概率质量函数：

NLP应用：词袋模型（Bag-of-Words）中单词的分布。

2. 连续型概率分布

（1）高斯分布（正态分布）

概率密度函数（PDF）：

NLP应用：潜在语义分析（LSA）中的降维技术（如PCA）。

（2）泊松分布（Poisson Distribution）

描述单位时间内事件发生次数的概率分布。
概率质量函数：

NLP应用：模拟罕见词在文档中的出现次数。

3. 概率分布的选择与建模

在NLP中，分布的选择需结合数据类型：

• 词频统计：多项分布或泊松分布。

• 文本长度建模：泊松分布或负二项分布。

• 连续特征（如词向量）：高斯分布。

四、参数估计：最大似然 vs 贝叶斯估计

1. 最大似然估计（MLE）

通过最大化似然函数求解参数：

 案例：估计单词“apple”在英文文档中的出现概率：

2. 贝叶斯估计

引入先验分布，计算参数的后验分布：

案例：在数据稀疏时，通过狄利克雷先验（Dirichlet Prior）平滑语言模型。

3. 平滑技术

• 拉普拉斯平滑（加一平滑）：避免零概率问题。

• 古德-图灵估计：调整罕见事件的概率。

五、NLP中的概率模型应用实例

1. 语言模型（Language Model）

• n-gram模型：基于马尔可夫假设，计算句子概率。
  例如，三元模型：

 

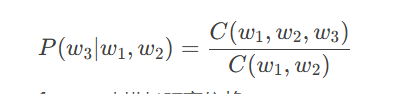
• 神经语言模型：使用RNN或Transformer建模长距离依赖。

2. 文本分类

• 主题模型（LDA）：基于多项分布和狄利克雷分布挖掘文档主题。

• 情感分析：通过逻辑回归（概率分类器）判断文本情感极性。

3. 机器翻译

• 基于短语的翻译模型：计算短语对齐的概率。

• 序列到序列模型：使用概率生成目标语言序列。

六、总结

概率论与统计学为NLP提供了处理不确定性和数据稀疏性的数学工具。从贝叶斯定理到概率分布，从参数估计到概率模型，这些概念构成了NLP算法的基石。随着深度学习的发展，概率思想与神经网络的结合（如变分自编码器、贝叶斯神经网络）进一步推动了NLP技术的进步。理解这些数学基础，不仅有助于掌握经典算法，更能为探索前沿技术奠定扎实的理论根基。