【图神经网络】图神经网络(GNN)学习笔记：基于GNN的图表示学习

最新推荐文章于 2025-02-26 23:41:35 发布

镰刀韭菜

最新推荐文章于 2025-02-26 23:41:35 发布

阅读量4.3k

点赞数 6

分类专栏：复杂网络与图学习文章标签：图神经网络图表示学习基于重构损失的GNN 基于对比损失的GNN DGI

本文链接：https://blog.csdn.net/ARPOSPF/article/details/122801406

版权

复杂网络与图学习专栏收录该内容

30 篇文章

订阅专栏

本文详细介绍了基于GNN的图表示学习，包括图表示学习原理、不同方法（分解、随机游走、深度学习）对比，重点讲解了GNN在重构损失（如GAE）和对比损失（如DGI）下的应用，以及其在图数据表示学习中的优势和挑战。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本文主要就基于GNN的无监督图表示学习进行详解。在实际的应用场景中，大量的数据标签往往具有很高的获取门槛，研究如何对图数据进行高效的无监督表示学习具有十分重要的价值。

1. 图表示学习

图表示学习（graph embedding）又可以称为网络表示学习（network embedding），或者称为网络嵌入，主要目标是将图数据转化成低维稠密的向量化表示，同时确保图数据中的某些性质在向量空间中也能够得到对应。
这里的图数据的表示可以是节点层面的，也可以是全图层面的，但是作为图数据的基本构成元素，节点的表示学习一直是图表示学习的主要对象。

一种图数据的表示如果能够包含丰富的语义信息，那么下游的相关任务，如点分类、边预测、图分类等，就都能得到相当优秀的输入特征，通常在这种情况下，直接选用线性分类器对任务进行学习。

不同的是，图表示学习的研究对象是图数据，图数据中蕴含着丰富的结构信息，这对应着图数据因内在关联而产生的一种非线性结构。因此，图表示学习具有以下两个重要作用：
（1）将图数据表示成线性空间中的向量。
（2）位置后的学习任务奠定基础。

图表示学习从方法上来说，可以分为基于分解的方法、基于随机游走的方法，以及基于深度学习的方法，如下图所示。而基于深度学习的方法的典型代表就是GNN相关的方法。
图表示学习的分类

早期，图节点的嵌入学习一般是基于分解的方法，通过对描述图数据结构信息的矩阵进行矩阵分解，将节点转化到低维向量空间中，同时保留结构上的相似性。描述结构信息的矩阵有：邻接矩阵、拉普拉斯矩阵、节点相似度矩阵。一般这类方法都有解析解，但是由于结果依赖相关矩阵的分解计算，因此，这类方法具有很高的时间和空间复杂度。
最近，词向量方法在语言表示上取得了很大成功，因此一些方法将图中随机游走产生的序列看作句子，将节点看作词，以此类比词向量方法从而学习出节点的表示，典型方法有：DeepWalk，Node2Vec等。
DeepWalk通过随机游走将图转化为节点序列，设置中心节点左右距离为 $w$ 的节点为上下文（context）。本质上，DeepWalk建模了中心节点与上下文节点之间的共现关系，这种关系的学习也采用了负采样的优化手段。另外DeepWalk与词向量方法具有十分一致的算法细节。
基于随机游走的方法的最大的优点是通过将图转化为序列的方式实现了大规模图的表示学习。缺点是：1. 图本身的结构信息没有被充分利用；2. 很难融合图中的属性信息进行表示学习。
基于深度学习的方法，例如，基于GNN的图表示学习具有以下优势：
（1）非常自然地融合了图的属性信息进行学习
（2）GNN本身作为一个可导的模块，能够嵌入到任意一个支持端对端学习的系统中去，使其能够与各个层面的有监督学习任务进行有机结合
（3）GNN的很多模型如GraphSAGE、MPNN等都是支持归纳学习的，多数情况下对于新数据的表示学习可以直接进行预测，而不必重新训练
（4）分解类的方法适用小图的学习，而GNN既保证了算法的工程性，又适应大规模图的学习任务。

类别	主要思想	代表模型	优点	缺点
基于分解的方法	对结构信息进行矩阵分解	-	-	具有很高的计算复杂度
基于随机游走的方法	将随机游走所产生的序列看作是句子，节点看作是词，类比词向量Skip-gram等模型的学习方法	DeepWalk、Node2Vec等	将图转化为序列，实现了大规模图的学习	①图本身的结构信息没有充分利用 ②很难融合属性信息进行表示学习
基于深度学习的方法	主要是使用基于GNN的方法进行表示学习	GraphSAGE、GAE、DGI等	①融合结构和属性信息进行表示学习 ②可以将表示学习和任务学习有机结合 ③能够适应大规模图	在模型深度、过平滑问题等方面仍面临挑战

2. 基于GNN的图表示学习

依据损失函数（Loss Function）的不同，基于GNN的无监督图表示学习方法可分为2类：
（1）基于重构损失的GNN
（2）基于对比损失的GNN

2.1 基于重构损失的GNN

主要思想类似于自编码器（AE），将节点之间的邻接关系进行重构学习，并将重构的矩阵与原矩阵进行相似度对比，来更新参数。因此，这类方法也叫作图自编码器（Graph Auto Encoder, GAE）。
$Z = G N N (X, A)$ $\hat{A}=\sigma(ZZ^T)$
其中 $Z$ 是所有节点的表示矩阵，这里借助GNN模型同时对图的属性信息和结构信息进行编码学习。 $\hat{A}$ 是重构后的邻接矩阵，这里适用向量的内积来表示节点之间的邻接关系。

图自编码器的重构损失定义如下： $Loss_{recon}=||\hat{A}-A||^2$

由于过平滑的问题，GNN可以轻易地将相邻节点学习出相似的表达，导致解码出来的邻接矩阵 $\hat{A}$ 能够很快趋近于原始邻接矩阵A，模型参数难以得到有效优化。因此，为了使GNN习得更加有效的数据分布式表示，必须对损失函数加上一些约束目标。即为了防止过平滑的问题，需要加入一些噪声，迫使模型从加噪的数据中学习到有用的信息用于恢复原数据：
（1）对原图数据的特征矩阵 $X$ 适当增加随机噪声或进行置零处理；
（2）对原图数据的邻接矩阵A删除适当比例的边，或者修改边上的权重值。

另外，也可以借助其他自编码器中的设计思路。例如变分图自编码器（Variational Graph Autoencoder, VGAE）。VGAE的基础框架和变分自编码器一样，不同的是使用了GNN来对图数据进行编码学习。从三个方向介绍其基础框架：
（1）推断模型（编码器）
${\textstyle \prod_{i=1}^{N}}q(z_i|X, A)$ $q(Z_i|X, A)=N(z_i|\mu _i, diag(\sigma_i^2))$ 与VAE不同，这里使用两个GNN对 $\mu, \sigma$ 进行拟合: $\mu=GNN_{\mu}(X, A), \log{\sigma}=GNN_\sigma(X, A)$
（2）生成模型（解码器）
$p(A|Z)=\prod_{i=1}^{N} \prod_{j=1}^{N}p(A_{ij}|z_i,z_j)$ $p(A_{ij}=1|z_i,z_j)=\sigma(z_i^T,z_j)$
这里也简单使用了两个节点表示向量的内积来拟合邻居关系。
（3）损失函数
$Loss=Loss_{recon}+Loss_{KL}=-E_{q(Z|X,A)}[\log{p(A|Z)}]+KL[q(Z|X,A)||p(Z)]$ 同样地，隐变量 $z$ 的先验分布选用标准正态分布：
$p(Z)=\prod_{i}p(z_i)=\prod_{i}N(z_i,\vec{0},\vec{I})$

VAE和GNN的结合,不仅可以被用来学习图数据的表示，更是提供了一个图生成模型的框架，能够在相关图生成的任务中得到应用。

2.2 基于对比损失的GNN

对比损失通常会设置一个评分函数 $D(\cdot)$ ，用来提高正样本的得分、降低负样本的得分。

类比词向量的学习，在图中，节点看作是词，上下文代表与节点有对应关系的对象。通常，图里的上下文从小到大依次可以是节点的邻居、节点所处的子图、全图。如何定义节点的“上下文”就成为一个值得研究的问题。目前为止共有3中定义方式：
（1）邻居作为上下文
（2）子图作为上下文
（3）全图作为上下文
不论是何种定义方式，我们都可以定义一个通用的损失函数: $Loss_{v_i}=-\log{(D(z_i,c))}+\log{(D(z_i,\bar{c}))}$ ,其中 $c$ 为上下文的表示向量 $\overline{c}$ 为非上下文的表示向量。

（1）邻居作为上下文
通过损失函数建模节点和邻居节点之间的关系，GraphSAGE中就使用了这种思路。主要思想类似于DeepWalk，将随机游走时与中心节点 $v_i$ 一起出现在固定窗口内的节点 $v_j$ 视为邻居，同时通过负采样的手段，将不符合该关系的节点作为负样本。与DeepWalk不同的是，节点的表示学习模型仍使用GNN，即： $Z = G N N (X, A)$ $Loss_{v_i}=\log{(1-\sigma(z_i^T,z_j))}+E_{v_n\sim P_n(v_i)}\log{(\sigma(z_i^T,z_{v_n}))}$ ，这里的 $p_n$ 是一个关于节点出现概率的负采样分布，得分函数使用向量内积加sigmoid函数，将分数限制在 $[0, 1]$ 内。该方法在优化目标上与图自编码器基本相同，但是这种负采样形式的对比优化并不需要自编码器一样显式地解码出邻接矩阵 $\hat{A}$ ，由于 $\hat{A}$ 破坏了原始邻接矩阵的稀疏性，因此该方法不需要承担 $O(N^2)$ 的空间复杂度。

（2）将子图作为上下文
邻居作为上下文强调的是节点之间的共现关系，但是有时候距离远的节点的结构未必没有相似之处，如此一来就缺乏对节点结构相似性的捕捉。

通常节点局部结构上的相似性是节点分类任务中一个比较关键的因素。
将子图作为上下文进行预测
对于一个中心节点，用一个GNN在其K阶子图上提取其表示向量，同时将处于中心节点 $r_1-hop$ 与 $r_2-hop$ 之间的节点定义为该中心节点的上下文锚点。如上图所示，设 $K=1,r_1=1,r_2=4$ ，用另一个GNN来提取每个节点作为上下文锚点时的表示向量，同时为了得到一个总的、固定长度的上下文表示向量，使用读出机制来聚合上下文锚点的表示向量。公式如下：
$Z=GNN(X, A), Z_{context}=GNN_{context}(X, A)$
$c_i=R(\{Z_{context}[j], \forall v_j是v_i的上下文锚点\})$
$Loss_{v_i}=\log{(1-\sigma(z_i^Tc_i))}+\log{(\sigma(z_i^Tc_{j|j\ne i}))}$

其中一共用到2个GNN。一个用来在 $K$ 阶子图上提取其特征向量 $Z$ ，另一个提取每个节点作为上下文锚点时的表示向量 $Z_{context}$ ，使用读出机制来聚合上下文锚点的表示向量 $c_i$ 。

（3）全图作为上下文
Deep Graph Infomax(DGI)的方法对图数据进行无监督表示学习，该方法实现了一种节点与全图之间的对比损失的学习机制。做法如下：
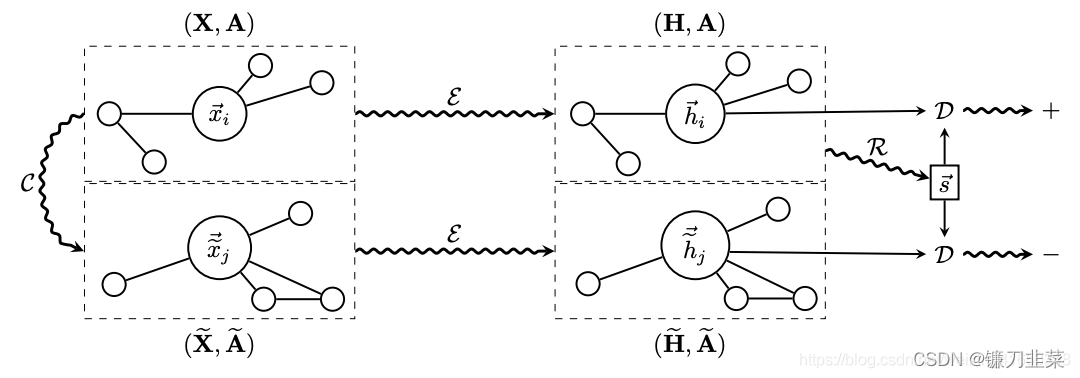
节点与全图对比损失学习机制
相关公式如下：
$\overline{Z}=GNN(X_{currupt}, A_{currupt})$ $s=Readout(\{z_i, \forall v_i\in V\})$ $Loss_{v_i}=\log{(1-D(z_i,s))}+\log{(D(\overline{z}_i,s))}$
其中 $A_{currupt},X_{currupt})$ 为加噪声构造的负采样样本。将正负样本送入同一个GNN中进行学习。使用读出机制得到全图的向量表示 $s$ 。

首先，为了得到负采样样本，需要对图数据进行相关扰动，得到 $A_{currupt},X_{currupt})$ 。然后将着两组图数据送到同一个GNN模型中进行学习。为了得到图的全局表示，使用读出机制对局部节点的信息进行整合。在最后的损失函数中，固定全图，对节点进行负采样的对比学习。

从互信息的角度看，通过一个统一的全局表示最大化全图与节点之间的互信息，可以在所有节点的表示之间建立一层更直接的联系。

同时在全图层面的无监督学习上，上述损失函数的负样本刚好相反，需要抽取其他图的表示 $\overline{s}$ 来代替，即 $Loss_{s}=E_{v_i\in G_s}\log{(1-D(z_i, s))}+E_{v_i\in G_s}\log{(D(z_i,\overline{s}))}$ ，此时，由于是全图层面的任务，希望通过上式让全图与其所有局部节点之间实现互信息最大化，即获得全图最有效、最具代表性的特征。