今天在2023年数模国赛E试题范文中学习到了贝叶斯估计,这里结合曾经学过的极大似然估计对贝叶斯估计的理解和解题思路做出梳理。
本文仅供作者自身梳理使用,若作为参考,本文语言广泛通俗、缺乏学术性,烦请批评指正!
极大似然估计
本人认为极大似然估计比较容易理解一点,所以先从这里讲起。
我们假设这样一个情形:抛掷一个不均匀的硬币,结果只有正面和反面之分。我们连续抛掷10次,得到了“正正正正反反反反反反”的结果。问抛掷一次硬币正面的概率是多少?
其实答案可以有很多种,但是总有一种是最佳的。那么,按照极大似然估计的方法,的值应该是多少呢?
答案就是:当我们的样本(也就是上述实验结果)出现的概率最大的时候就是的取值。如果是本次实验中出现的情况,那就是使得
取最大值的
就是我们所求的结果。通俗理解就是:既然我们的样本是最终的结果,那么他一定是所有出现情况下概率最大的那种。这就是极大似然估计。
这个例子中有如下的特点:
- 我们假设了其服从0-1分布;
- 但是分布的概率是未知的(那我们设正面的概率为
,反面就是1-
);
- 每一次抛硬币之间的结果并不相关。
在其他的极大似然函数当中,也要满足以上的部分特点:
- 变量的形式是已知的(比如说我们知道变量服从正态分布或者是0-1分布等等);
- 但是其中的参数是未知的(正态分布的均值和方差是未知的);
- 每一次抽样的结果是独立的。此时,D的分布函数为:
即当为某一值时所有独立事件概率的乘积,这个乘积随着
的变化而变化。
这样的话我们就可以用一个有带参()的函数表示出当前样本出现的概率P,然后求出当参数为多少时P的值最大的。这个参数的值就是极大似然估计的值。
贝叶斯估计
贝叶斯估计的目的和极大似然估计是相同的,都是为了解出已知分布的未知参数。但是两者对应当是多少的衡量标准并不相同:通过极大似然估计,我们应该能够求出唯一的
使得P是最大值,比否定了其他
的取值;但贝叶斯估计则不然,其并不认为
应当是使得当前样本出现的概率最大时
的值,就像是上述抛硬币的例子,使得上述样本出现的概率最大的概率是0.6,但其实也可以是其他的值,比如0.5,但只是使得样本出现的概率相对较小而已。
既然是未知的随机变量,那他也会有一定的分布函数或密度函数存在。
问题来了【求解的关键】:
的分布函数和密度函数应当是什么形式?
的分布函数和密度函数之后,我们最终怎样确定
的值(即估计值
)?
第一问比较难以解答,但是对于第二个问而言,我们基于平方误差损失函数将最终的值敲定为d 期望,即:
(证明过程可以看前文的链接)
公式当中(密度函数)就是第一问提出的问题。当然,我们难以直接求解密度函数因为其函数值不具有意义,但是我们可以求解分布函数
再将其转化为
。
【关键】如何求解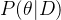 ?
?
不好解,可以再次转变形式。利用贝叶斯公式(条件概率)转化关系为:
问题就转化成了求:和
。
求解在上文【极大似然估计】的部分已经提到了,其公式为:
其现实意义就是在取不同值时样本D出现的概率函数(以
为自变量,遵从已知分布)。
我们一般称之为先验概率,一般都是已知的,或者是通过和样本无关的信息当中确定。之于在建模当中如何确定
还要进一步探索(留着以后解决)。
一个总结
上面的过程是倒着说的,从求解的任务出发,接着确定其估计值的标准,再计算其分布函数。按照一般解题思路来讲应当如下:

这就是贝叶斯估计的全部内容啦!希望过几天还记得!







 本文通过对比分析贝叶斯估计和极大似然估计在参数估计中的方法,以抛硬币为例,解释了两者原理,并讨论了先验知识在贝叶斯估计中的应用。最后概述了贝叶斯估计的一般解题步骤。
本文通过对比分析贝叶斯估计和极大似然估计在参数估计中的方法,以抛硬币为例,解释了两者原理,并讨论了先验知识在贝叶斯估计中的应用。最后概述了贝叶斯估计的一般解题步骤。
 https://blog.csdn.net/zengxiantao1994/article/details/72889732
https://blog.csdn.net/zengxiantao1994/article/details/72889732













 1193
1193

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








