人类学家已经使用Voronoi图来描述不同文化的影响区域。由晶体学家解释某些晶体和金属的结构;由生态学家研究植物之间的竞争;由经济学家为美国经济中的市场建模...
介绍
假设您生活在沙漠中,那里唯一的水源是到零星散布各处的泉水。对于每个泉水,您都想确定最接近该泉水的位置。结果可能是一张地图,如此处所示,其中地形被划分为最接近各个泉水的位置区域。
{每块区域所对应的最接近的泉水,即为其包含其内的泉水}

这样的地图经常出现在各种应用程序中,并且名称很多。对于数学家来说,它们被称为Voronoi图。泉水的位置被普遍地称为站点(Sites),而最接近该站点的点集就是其Voronoi单元。这里一个小程序,显示图随着站点的移动而变化。
Voronoi图是很自然的构造,似乎它们或类似的东西已经使用了很长时间了。例如,笛卡尔(Descartes)在演示物质在整个太阳系中的分布方式时包括了下图。
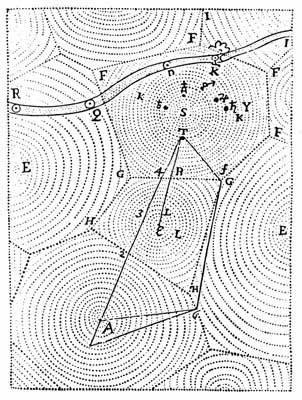
从那时起,人类学家就开始使用Voronoi图来描述不同文化的影响区域。由晶体学家解释某些晶体和金属的结构;由生态学家研究植物之间的竞争;并由经济学家为美国经济中的市场建模。
特别值得注意的应用出现在约翰·斯诺(John Snow)对1854年伦敦霍乱疫情的分析中。以下地图包括在斯诺(Snow)关于威斯敏斯特大教堂圣詹姆斯教区霍乱疫情的报告中(1854年秋天),显示了死亡人数的分布由于霍乱。每个小条表示该地址处的死亡人数。
 |
| 点击放大 |
然后,斯诺考虑了饮用水的来源,遍布整个城市的水泵,并划出了一条标有“宽街泵与其他水泵之间的距离相等的边界”的线,从本质上说明了宽街泵的Voronoi单元。

该地图支持斯诺的假说,即霍乱死亡与受污染的水有关(在本例中为宽街泵)。斯诺建议当局移开泵的把手,此后霍乱爆发迅速结束。由于斯诺的工作帮助发展了现代流行病学领域,因此该地图被称为“最著名的19世纪疾病地图”。
构造Voronoi图
在本文中,我们将想象我们得到的站点是有限的,并且将看到如何有效地构建其Voronoi图。
首先,当遇到这个问题时,成对地考虑站点似乎是最直接能想到的。一个重要的事实是,如果我们给出了两个点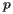 和
和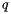 ,那么连接这两个点的线段的垂直平分线就是由与
,那么连接这两个点的线段的垂直平分线就是由与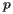 以及与
以及与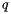 相同距离的点组成的。
相同距离的点组成的。

实际上,我们可能想将垂直等分线视为将平面分为两个半平面,一个半平面包含更靠近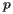 的点,另一个包含更靠近的点
的点,另一个包含更靠近的点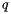 。我们将用
。我们将用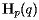 来表示包含更接近
来表示包含更接近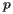 点的半平面。
点的半平面。
 构造Voronoi图的过程似乎非常简单:要找到最接近站点
构造Voronoi图的过程似乎非常简单:要找到最接近站点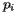 的点集,我们只需获取所有半平面的交点
的点集,我们只需获取所有半平面的交点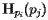 即可。也就是说,包含站点
即可。也就是说,包含站点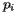 的Voronoi单元由
的Voronoi单元由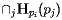 给出。
给出。
当然,如上图所示,我们在这里所做的一些工作不是必需的; 也就是说,某些距离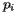 相对较远的站点对
相对较远的站点对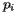 的Voronoi单元没有影响。 实际上,当存在大量站点时,我们期望一个特定站点的Voronoi单元由相对较少的其他站点确定。
的Voronoi单元没有影响。 实际上,当存在大量站点时,我们期望一个特定站点的Voronoi单元由相对较少的其他站点确定。
在使用这种方法时,如果我们有我们 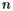 个站点,我们需要考虑其他
个站点,我们需要考虑其他 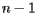 个站点以查找特定站点的Voronoi单元。 由于每个站点都有自己的Voronoi单元,因此我们需要构建
个站点以查找特定站点的Voronoi单元。 由于每个站点都有自己的Voronoi单元,因此我们需要构建 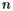 个 Voronoi单元,这将需要我们构建
个 Voronoi单元,这将需要我们构建 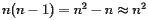 个半平面。 例如,如果我们有1000个点,则需要构造大约一百万个半平面。
个半平面。 例如,如果我们有1000个点,则需要构造大约一百万个半平面。
看来,实现此方法将需要我们做很多工作,但是其中许多工作是不必要的。 一个自然的问题就是,是否有一种更有效的方法来计算Voronoi图。
Fortune 算法
实际上,有几种查找Voronoi图的方法,其中一种被称为Fortune算法。
该算法基于以下聪明的想法:我们不考虑各个站点之间的距离,而是引入一条在平面中移动的线,并使用该线促成更高效的距离比较。 我们称这条线为扫掠线,并试图通过其平面扫掠来拆分Voronoi图。
首先,我们要记住的一点是,假设给定一个点 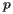 和一条直线
和一条直线 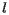 (不包含点
(不包含点 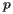 ),那么与点
),那么与点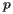 和直线
和直线 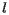 距离相等的顶点将形成一条抛物线。
距离相等的顶点将形成一条抛物线。

我们将用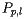 来表示这条抛物线。如前所述,使用抛物线将平面划分为两个区域是有帮助的:一个区域由更接近
来表示这条抛物线。如前所述,使用抛物线将平面划分为两个区域是有帮助的:一个区域由更接近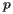 的点组成,而另一个区域则由更接近
的点组成,而另一个区域则由更接近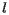 的点组成。
的点组成。
这是很重要的一点,所以让我们说的更清楚一点。 考虑一点 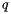 ,其坐标是
,其坐标是 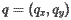 ,它与点
,它与点 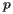 距离用
距离用 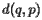 表示 。 在下文中,扫掠线将始终为水平线; 我们将其垂直坐标称为
表示 。 在下文中,扫掠线将始终为水平线; 我们将其垂直坐标称为 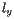 ,那么
,那么 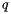 和
和 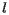 之间的距离是
之间的距离是 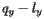 。 点
。 点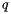 位于抛物线
位于抛物线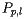 上的条件是:
上的条件是:
![\ [d(q,p)= q_y-l_y \]](https://i-blog.csdnimg.cn/blog_migrate/be19621813d1b1ca9caf61c38ac23bd5.gif)
或者,更一般而言
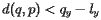 如果
如果 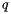 位于上方
位于上方 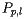
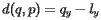 如果
如果 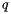 位于
位于 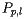
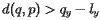 如果
如果 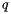 位于下面
位于下面 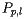
现在,水平扫掠线 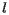 将向下穿过平面。 在任何时候,我们只会考虑位于扫掠线上方的站点以及这些站点定义的抛物线
将向下穿过平面。 在任何时候,我们只会考虑位于扫掠线上方的站点以及这些站点定义的抛物线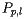 。 例如在给定下方左图所示的站点集合以及扫掠线位置时,我们将考虑如右图所示的抛物线。
。 例如在给定下方左图所示的站点集合以及扫掠线位置时,我们将考虑如右图所示的抛物线。


现在,我们可以介绍Fortune算法的真正明星:海滩线,它是由最低抛物线弧组合形成的曲线。 也就是说,任何垂直线都将穿过若干抛物线。 海滩线上的点是垂直线穿过的抛物线点中的最低点。 请注意,组成海滩线的每条弧线都与扫掠线上方的某个站点相关联。

海滩线非常适合构建Voronoi图。举例来说,如果一个点位于海滩线的上方,那么相对于扫掠线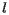 来说,它一定更接近
来说,它一定更接近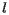 上方的某个站点。这意味着此点一定位于扫掠线已穿过的某个站点的Voronoi单元中。 因此,海滩线上方的Voronoi图可由扫掠线上方的站点所确定。
上方的某个站点。这意味着此点一定位于扫掠线已穿过的某个站点的Voronoi单元中。 因此,海滩线上方的Voronoi图可由扫掠线上方的站点所确定。
该是看看动画演示的时候了,该动画显示了扫掠线向下移动扫过平面时海滩线如何变化。
现在,让我们确定海滩线何时经过某个任意顶点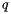 。假设相对所有其它站点,顶点
。假设相对所有其它站点,顶点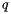 都更接近站点
都更接近站点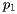 {假设
{假设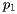 是一个海滩线站点,也就是,在当前扫掠线位置情况下,其抛物线仍然属于海滩线一部分的站点};也就是说,对于所有其他站点
是一个海滩线站点,也就是,在当前扫掠线位置情况下,其抛物线仍然属于海滩线一部分的站点};也就是说,对于所有其他站点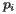 来说,
来说,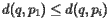 成立,那么顶点
成立,那么顶点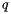 处于抛物线
处于抛物线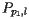 上的条件可以表示为:
上的条件可以表示为:
![\ [d(q,p_1)= q_y-l_y \]](https://i-blog.csdnimg.cn/blog_migrate/333cb00756e4660b0df886f84c64034a.gif)
也就是:
![\ [d(q,p_i)\ geq d(q,p_1)= q_y-l_y \]](https://i-blog.csdnimg.cn/blog_migrate/e7dfbd2430f427f8b427e79e7c82d51c.gif)
这意味着,当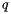 出现在抛物线
出现在抛物线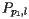 上时,它不能在另一个抛物线
上时,它不能在另一个抛物线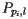 上。因此,当
上。因此,当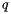 出现在抛物线
出现在抛物线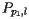 上时,它在海滩线上。让我们总结一下这一重要的结论:
上时,它在海滩线上。让我们总结一下这一重要的结论:
当一个点出现在海滩线上时,它位于与其最近的站点相关联的抛物线弧上。
海滩线上位于两个抛物线弧上的点称为断点。根据我们观察的结果表明,断点是距离两个站点最近的点。换一种说法,
断点位于Voronoi图的边缘。
这意味着,当扫掠线沿平面向下移动时,断点将扫出Voronoi图的边缘。因此,要构建Voronoi图,我们只需要跟踪断点即可。这是一个动画,显示了断点如何形成Voronoi图的边缘。
寻找边缘
到目前为止,我们已经看到,如果要构建Voronoi图的边缘,我们只需要在扫掠线沿平面向下移动时跟踪相应的一对断点即可。这样做的第一步,是检测何时构造了一对断点。如下图所示,当在海滩线上添加新弧线时,就会发生这种情况。



换句话说,当扫掠线经过新站点时,对应于Voronoi图中一条边的一对断点将出现在海滩线上。我们将这种情况称为站点事件。
寻找顶点
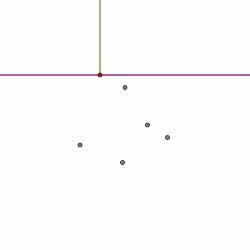
随着扫描线向下移动,这些断点沿着Voronoi图的边缘连续移动,直到到达该Voronoi图中的顶点为止。当沿着海滩线的抛物线弧之一消失时,就会发生这种情况。在以下图片序列中,请注意,从左图中的右数第二个抛物线弧(最小的弧)消失了。


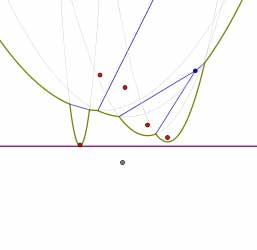
很容易检测到海滩线上出现新的抛物线弧:它们在扫掠线穿过某个地点时发生。同样,也容易检测到抛物线弧的消失。当抛物线弧缩小到一个点时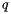 ,该点
,该点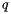 将位于三个抛物线上:包含一个消失的弧,另外包含两侧各一个抛物线弧。这意味着
将位于三个抛物线上:包含一个消失的弧,另外包含两侧各一个抛物线弧。这意味着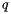 与对应于这些抛物线的三个站点等距,因此这三个站点位于以
与对应于这些抛物线的三个站点等距,因此这三个站点位于以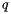 为半径的圆上。因此,当扫掠线穿过该圆的底部时,我们找到了顶点
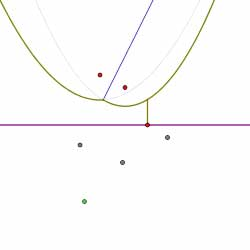
为半径的圆上。因此,当扫掠线穿过该圆的底部时,我们找到了顶点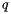 。
。

我们称这种情况为圆形事件。因此,图中的更改如下所示:



注意,圆形事件也会创建新的边。这与以下事实相对应:我们有一个新的断点形成,该断点是与消失的弧所相邻的两个抛物线弧的交点。
算法
现在,我们拥有了解Fortune算法所需的一切。要检测Voronoi图中的边缘和顶点,只需找出海滩线上抛物线弧的出现和消失即可。因此,我们将通过想象我们从左到右走动并记录产生其抛物线弧的位置顺序来跟踪海滩线。我们知道,直到扫描线到达站点事件或圆形事件,此顺序才会改变。同样,通过记录海滩线上抛物线弧的邻接点,断点也被顺带记录。
如果扫掠线遇到的下一个事件是站点事件,我们只需按照相应的抛物线弧在海滩线上出现的顺序,将新站点插入站点列表即可。然后,我们将在图表中记录这样的信息:增加一条Voronoi图边缘。
如果扫掠线遇到的下一个事件是圆形事件,那么我们在图中记录这样的信息:增加一个Voronoi图顶点,并且该顶点对应于已合在一起的两个断点的边的端点。我们还记录了与圆形事件导致的新断点相对应的新边。
无论我们遇到站点事件还是圆形事件,我们始终都会检查是否在海滩线上添加了新的三重抛物线弧,这可能会导致未来的圆形事件。如果导致该事件的抛物线弧的三元组在事件之后不再存在,我们也有可能将其排除在考虑范围之外。
这样,就通过考虑事件的有限种顺序来构造该图。下面显示的是计算所有站点集合的Voronoi图的事件序列。圆圈事件由绿点表示。










摘要
Fortune算法是一种非常有效的计算Voronoi图的方法。无论我们使用哪种算法,都应该知道,站点越多,查找Voronoi图也就需要越多的计算工作。然而,我们需要更加精确地评估计算复杂度。之前,我们考虑了一种算法,该算法通过与包含该位点的每个半平面相交来找到每个Voronoi单元,从而找到Voronoi图。如果站点数目为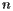 ,则实施此算法所需的步骤数与
,则实施此算法所需的步骤数与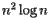 成比例。但是,对于典型的图表,实现Fortune算法所需的步骤数与
成比例。但是,对于典型的图表,实现Fortune算法所需的步骤数与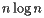 成正比,这代表了相当大的改进。下图根据站点数量比较了这两种算法的计算量。
成正比,这代表了相当大的改进。下图根据站点数量比较了这两种算法的计算量。

























 5345
5345

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








