文章目录
- Part 1 不定积分
- Part 2 定积分及其应用
- 记忆内容
- 题型
- 1 概念和性质
- 2 定积分定义求n项和极限
- 3 由 f ( x ) \,f(x)\, f(x)含自身定积分的表达式,求 f ( x ) \,f(x) f(x) (设 A \,A A)
- 4 变积分限函数相关问题
- 5 定积分的计算
- 6 定积分证明
- 7 反常积分计算
- 8 定积分的几何应用
Part 1 不定积分
记忆内容
1 基本公式
1. 最基本的:
∫
k
d
x
=
k
x
+
C
\int k\text{d}x=kx+C
∫kdx=kx+C
∫
x
a
d
x
=
1
a
+
1
x
a
+
1
+
C
(
a
≠
−
1
)
,
∫
d
x
x
=
ln
∣
x
∣
+
C
(
x
≠
0
)
\int x^a\text{d}x=\frac{1}{a+1}x^{a+1}+C\;\;(a\neq-1),\int\frac{\text{d}x}{x}=\text{ln}|x|+C\;\;(x\neq 0)
∫xadx=a+11xa+1+C(a=−1),∫xdx=ln∣x∣+C(x=0)
∫
a
x
d
x
=
a
x
ln
a
+
C
(
a
>
0
,
a
≠
1
)
,
∫
e
x
d
x
=
e
x
+
C
\int a^x\text{d}x=\frac{a^x}{\text{ln}a}+C\;\;(a>0,a\neq1),\int e^x\text{d}x=e^x+C
∫axdx=lnaax+C(a>0,a=1),∫exdx=ex+C
∫
sin
x
d
x
=
−
cos
x
+
C
,
∫
cos
x
d
x
=
sin
x
+
C
\int \text{sin}x\text{d}x=-\text{cos}x+C,\int \text{cos}x\text{d}x=\text{sin}x+C
∫sinxdx=−cosx+C,∫cosxdx=sinx+C
∫
sec
2
x
d
x
=
tan
x
+
C
,
∫
csc
2
x
d
x
=
−
cot
x
+
C
\int \text{sec}^2x\text{d}x=\text{tan}x+C,\int \text{csc}^2x\text{d}x=-\text{cot}x+C
∫sec2xdx=tanx+C,∫csc2xdx=−cotx+C
∫
sec
x
⋅
tan
x
d
x
=
sec
x
+
C
,
∫
csc
x
⋅
cot
x
d
x
=
−
csc
x
+
C
\int \text{sec}x\cdot\text{tan}x\text{d}x=\text{sec}x+C,\int \text{csc}x\cdot\text{cot}x\text{d}x=-\text{csc}x+C
∫secx⋅tanxdx=secx+C,∫cscx⋅cotxdx=−cscx+C
∫
d
x
1
−
x
2
d
x
=
arcsin
x
+
C
\int \frac{\text{d}x}{\sqrt{1-x^2}}{d}x=\text{arcsin}x+C
∫1−x2dxdx=arcsinx+C
∫
1
1
+
x
2
d
x
=
arctan
x
+
C
\int \frac{1}{1+x^2}{d}x=\text{arctan}x+C
∫1+x21dx=arctanx+C
2. 需要重点记忆:
∫
tan
x
d
x
=
−
ln
∣
cos
x
∣
+
C
,
∫
cot
x
d
x
=
ln
∣
sin
x
∣
+
C
\int \text{tan}x\text{d}x=-\text{ln}\bigg|\text{cos}x\bigg|+C,\int \text{cot}x\text{d}x=\text{ln}\bigg|\text{sin}x\bigg|+C
∫tanxdx=−ln∣∣∣∣cosx∣∣∣∣+C,∫cotxdx=ln∣∣∣∣sinx∣∣∣∣+C
∫
sec
x
d
x
=
ln
∣
sec
x
+
tan
x
∣
+
C
,
∫
csc
x
d
x
=
ln
∣
csc
x
−
cot
x
∣
+
C
\int \text{sec}x\text{d}x=\text{ln}\bigg|\text{sec}x+\text{tan}x\bigg|+C,\int \text{csc}x\text{d}x=\text{ln}\bigg|\text{csc}x-\text{cot}x\bigg|+C
∫secxdx=ln∣∣∣∣secx+tanx∣∣∣∣+C,∫cscxdx=ln∣∣∣∣cscx−cotx∣∣∣∣+C
∫
d
x
a
2
−
x
2
=
arcsin
x
a
+
C
(
a
>
0
)
\int \frac{\text{d}x}{\sqrt{a^2-x^2}}=\text{arcsin}\frac{x}{a}+C\;\;(a>0)
∫a2−x2dx=arcsinax+C(a>0)
∫
d
x
x
2
−
a
2
=
ln
∣
x
+
x
2
−
a
2
∣
+
C
,
∫
d
x
x
2
+
a
2
=
ln
(
x
+
x
2
+
a
2
)
+
C
\int \frac{\text{d}x}{\sqrt{x^2-a^2}}=\text{ln}\bigg|x+\sqrt{x^2-a^2}\bigg|+C,\int \frac{\text{d}x}{\sqrt{x^2+a^2}}=\text{ln}\big(x+\sqrt{x^2+a^2}\big)+C
∫x2−a2dx=ln∣∣∣∣x+x2−a2∣∣∣∣+C,∫x2+a2dx=ln(x+x2+a2)+C
∫
d
x
x
2
+
a
2
=
1
a
arctan
x
a
+
C
(
a
≠
0
)
\int \frac{\text{d}x}{x^2+a^2}=\frac{1}{a}\text{arctan}\frac{x}{a}+C\;\;(a\neq 0)
∫x2+a2dx=a1arctanax+C(a=0)
∫
d
x
x
2
−
a
2
=
1
2
a
ln
∣
x
−
a
x
+
a
∣
+
C
\int \frac{\text{d}x}{x^2-a^2}=\frac{1}{2a}\text{ln}\bigg|\frac{x-a}{x+a}\bigg|+C
∫x2−a2dx=2a1ln∣∣∣∣x+ax−a∣∣∣∣+C
∫
a
2
−
x
2
d
x
=
a
2
2
arcsin
x
a
+
x
2
a
2
−
x
2
+
C
\int \sqrt{a^2-x^2}{\text{d}x}=\frac{a^2}{2}\text{arcsin}\frac{x}{a}+\frac{x}{2}\sqrt{a^2-x^2}+C
∫a2−x2dx=2a2arcsinax+2xa2−x2+C
∫
e
x
[
f
(
x
)
+
f
′
(
x
)
]
d
x
=
e
x
f
(
x
)
+
C
\int e^x[f(x)+f'(x)]\text{d}x=e^xf(x)+C
∫ex[f(x)+f′(x)]dx=exf(x)+C
2 基本积分法
(一) 换元积分法
第一类换元积分法
将一个 x \,x\, x的复杂表达式用一个 t \,t\, t进行替换求积分,最后把 x \,x\, x代回去.
基本手法 (应该极其熟练):
∫
x
n
−
1
f
(
a
x
n
+
b
)
d
x
=
1
n
a
∫
f
(
a
x
n
+
b
)
d
(
a
x
n
+
b
)
(
a
≠
0
)
\int x^{n-1}f(ax^n+b)\text{d}x=\frac{1}{na}\int f(ax^n+b)\text{d}(ax^{n}+b)\;\;(a\neq 0)
∫xn−1f(axn+b)dx=na1∫f(axn+b)d(axn+b)(a=0)
∫
f
(
x
)
x
d
x
=
2
∫
f
(
x
)
2
x
d
x
=
2
∫
f
(
x
)
d
(
x
)
\int\frac{f(x)}{\sqrt{x}}\text{d}x=2\int\frac{f(x)}{2\sqrt{x}}\text{d}x=2\int f(x)\text{d}(\sqrt{x})
∫xf(x)dx=2∫2xf(x)dx=2∫f(x)d(x)
∫
1
x
2
d
x
=
−
∫
1
x
d
x
\int\frac{1}{x^2}\text{d}x=-\int\frac{1}{x}\text{d}x
∫x21dx=−∫x1dx
∫
f
(
x
)
x
d
x
=
∫
f
(
x
)
d
(
ln
x
)
\int \frac{f(x)}{x}\text{d}x=\int f(x)\text{d}(\text{ln}x)
∫xf(x)dx=∫f(x)d(lnx)
∫
e
x
f
(
x
)
d
x
=
∫
f
(
x
)
d
(
e
x
)
\int e^xf(x)\text{d}x=\int f(x)\text{d}(e^x)
∫exf(x)dx=∫f(x)d(ex)
∫
(
1
+
x
)
e
x
f
(
x
)
d
x
=
∫
f
(
x
)
d
(
x
e
x
)
\int (1+x)e^xf(x)\text{d}x=\int f(x)\text{d}(xe^x)
∫(1+x)exf(x)dx=∫f(x)d(xex)
∫
(
1
+
ln
x
)
f
(
x
)
d
x
=
∫
f
(
x
)
d
(
x
ln
x
)
\int(1+\text{ln}x)f(x)\text{d}x=\int f(x)\text{d}(x\text{ln}x)
∫(1+lnx)f(x)dx=∫f(x)d(xlnx)
∫
(
1
−
ln
x
)
f
(
x
)
d
x
=
∫
(
1
+
ln
x
)
f
(
x
)
x
2
⋅
x
2
d
x
=
∫
x
2
f
(
x
)
d
(
ln
x
x
)
\int(1-\text{ln}x)f(x)\text{d}x=\int\frac{(1+\text{ln}x)f(x)}{x^2}\cdot x^2\text{d}x=\int x^2f(x)\text{d}(\frac{\text{ln}x}{x})
∫(1−lnx)f(x)dx=∫x2(1+lnx)f(x)⋅x2dx=∫x2f(x)d(xlnx)
∫
f
(
x
)
sin
x
d
x
=
−
∫
f
(
x
)
d
(
cos
x
)
,
∫
f
(
x
)
cos
x
d
x
=
∫
f
(
x
)
d
(
sin
x
)
\int f(x)\text{sin}x\text{d}x=-\int f(x)\text{d}(\text{cos}x),\int f(x)\text{cos}x\text{d}x=\int f(x)\text{d}(\text{sin}x)
∫f(x)sinxdx=−∫f(x)d(cosx),∫f(x)cosxdx=∫f(x)d(sinx)
∫
f
(
x
)
sec
2
x
d
x
=
∫
f
(
x
)
d
(
tan
x
)
,
∫
f
(
x
)
csc
2
x
d
x
=
−
∫
f
(
x
)
d
(
cot
x
)
\int f(x)\text{sec}^2x\text{d}x=\int f(x)\text{d}(\text{tan}x),\int f(x)\text{csc}^2x\text{d}x=-\int f(x)\text{d}(\text{cot}x)
∫f(x)sec2xdx=∫f(x)d(tanx),∫f(x)csc2xdx=−∫f(x)d(cotx)
∫
f
(
x
)
sec
x
⋅
tan
x
d
x
=
∫
f
(
x
)
d
(
sec
x
)
,
∫
f
(
x
)
csc
x
⋅
cot
x
d
x
=
−
∫
f
(
x
)
d
(
csc
x
)
\int f(x)\text{sec}x\cdot\text{tan}x\text{d}x=\int f(x)\text{d}(\text{sec}x),\int f(x)\text{csc}x\cdot\text{cot}x\text{d}x=-\int f(x)\text{d}(\text{csc}x)
∫f(x)secx⋅tanxdx=∫f(x)d(secx),∫f(x)cscx⋅cotxdx=−∫f(x)d(cscx)
∫ f ( x ) 1 − x 2 d x = ∫ f ( x ) d ( arcsin x ) \int\frac{f(x)}{\sqrt{1-x^2}}\text{d}x=\int f(x)\text{d}(\text{arcsin}x) ∫1−x2f(x)dx=∫f(x)d(arcsinx) ∫ f ( x ) 1 + x 2 d x = ∫ f ( x ) d ( arctan x ) \int\frac{f(x)}{1+x^2}\text{d}x=\int f(x)\text{d}(\text{arctan}x) ∫1+x2f(x)dx=∫f(x)d(arctanx) ∫ 1 x ln x f ( x ) d x = ∫ f ( x ) d ( lnln x ) \int\frac{1}{x\text{ln}x}f(x)\text{d}x=\int f(x)\text{d}(\text{ln}\text{ln}x) ∫xlnx1f(x)dx=∫f(x)d(lnlnx) ∫ 1 x ln x ⋅ lnln x f ( x ) d x = ∫ f ( x ) d ( lnlnln x ) \int\frac{1}{x\text{ln}x\cdot\text{lnln}x}f(x)\text{d}x=\int f(x)\text{d}(\text{ln}\text{ln}\text{ln}x) ∫xlnx⋅lnlnx1f(x)dx=∫f(x)d(lnlnlnx) ∫ e sin x cos x f ( x ) d x = ∫ f ( x ) d ( e sin x ) \int e^{\text{sin}x}\text{cos}xf(x)\text{d}x=\int f(x)\text{d}(e^{\text{sin}x}) ∫esinxcosxf(x)dx=∫f(x)d(esinx)
配方法 (通常不是最简单的方法):
∫
d
x
x
(
4
−
x
)
=
∫
d
(
x
−
2
)
2
2
−
(
x
−
2
)
2
\int\frac{\text{d}x}{\sqrt{x(4-x)}}=\int\frac{\text{d}(x-2)}{\sqrt{2^2-(x-2)^2}}
∫x(4−x)dx=∫22−(x−2)2d(x−2)
高级手法 (以下方法不便归纳,用法也很灵活,熟悉即可)
(1) 分母出现
1
+
x
4
{\color{Blue} \,1+x^4}
1+x4:
(
x
±
1
x
)
2
=
x
2
+
1
x
2
±
2
{\color{Purple} (x\pm\frac{1}{x})^2=x^2+\frac{1}{x^2}\pm2}
(x±x1)2=x2+x21±2
∫
x
2
+
1
x
4
+
1
d
x
=
∫
1
+
1
x
2
x
2
+
1
x
2
d
x
=
∫
d
(
x
−
1
x
)
(
x
−
1
x
)
2
+
(
2
)
2
\int\frac{x^2+1}{x^4+1}\text{d}x=\int\frac{1+\frac{1}{x^2}}{x^2+\frac{1}{x^2}}\text{d}x=\int\frac{\text{d}(x-\frac{1}{x})}{(x-\frac{1}{x})^2+(\sqrt{2})^2}
∫x4+1x2+1dx=∫x2+x211+x21dx=∫(x−x1)2+(2)2d(x−x1)
∫
x
2
−
1
1
+
x
4
d
x
=
∫
1
−
1
x
2
1
x
2
+
x
2
d
x
=
∫
d
(
x
+
1
x
)
(
x
+
1
x
)
2
−
(
2
)
2
\int\frac{x^2-1}{1+x^4}\text{d}x=\int\frac{1-\frac{1}{x^2}}{\frac{1}{x^2}+x^2}\text{d}x=\int\frac{\text{d}(x+\frac{1}{x})}{(x+\frac{1}{x})^2-(\sqrt{2})^2}
∫1+x4x2−1dx=∫x21+x21−x21dx=∫(x+x1)2−(2)2d(x+x1)
∫
1
1
+
x
4
d
x
=
1
2
(
∫
x
2
+
1
1
+
x
4
d
x
−
∫
x
2
−
1
1
+
x
4
d
x
)
\int\frac{1}{1+x^4}\text{d}x=\frac{1}{2}\bigg(\int\frac{x^2+1}{1+x^4}\text{d}x-\int\frac{x^2-1}{1+x^4}\text{d}x\bigg)
∫1+x41dx=21(∫1+x4x2+1dx−∫1+x4x2−1dx)
(2) 几种重要 凑 齐 {\color{Blue}凑齐} 凑齐的思路:
a. 凑分母:
∫
x
e
x
(
x
+
1
)
2
d
x
=
∫
(
x
+
1
)
−
1
(
x
+
1
)
2
e
x
d
x
=
∫
[
1
x
+
1
−
1
(
x
+
1
)
2
]
e
x
=
e
x
x
+
1
+
C
\int\frac{xe^x}{(x+1)^2}\text{d}x=\int\frac{(x+1)-1}{(x+1)^2}e^x\text{d}x=\int\bigg[\frac{1}{x+1}-\frac{1}{(x+1)^2}\bigg]e^x=\frac{e^x}{x+1}+C
∫(x+1)2xexdx=∫(x+1)2(x+1)−1exdx=∫[x+11−(x+1)21]ex=x+1ex+C
∫
x
3
1
+
x
2
d
x
=
∫
x
3
+
x
−
x
1
+
x
2
d
x
\int\frac{x^3}{\sqrt{1+x^2}}\text{d}x=\int\frac{x^3+x-x}{\sqrt{1+x^2}}\text{d}x
∫1+x2x3dx=∫1+x2x3+x−xdx
b. 凑分母的导数:
∫
x
−
2
x
2
+
x
+
2
d
x
=
1
2
∫
2
x
+
1
−
5
x
2
+
x
+
2
d
x
=
1
2
∫
d
(
x
2
+
x
+
2
)
x
2
+
x
+
2
−
5
2
∫
d
(
x
+
1
2
)
(
x
+
1
2
)
2
+
7
4
\int\frac{x-2}{x^2+x+2}\text{d}x=\frac{1}{2}\int\frac{2x+1-5}{x^2+x+2}\text{d}x=\frac{1}{2}\int\frac{\text{d}(x^2+x+2)}{x^2+x+2}-\frac{5}{2}\int\frac{\text{d}(x+\frac{1}{2})}{(x+\frac{1}{2})^2+\frac{7}{4}}
∫x2+x+2x−2dx=21∫x2+x+22x+1−5dx=21∫x2+x+2d(x2+x+2)−25∫(x+21)2+47d(x+21)
c. 凑分母的次数:
∫
d
x
x
(
x
4
+
2
)
=
∫
x
3
x
4
(
x
4
+
2
)
=
1
4
∫
d
(
x
4
+
2
)
x
4
(
x
4
+
2
)
\int\frac{\text{d}x}{x(x^4+2)}=\int\frac{x^3}{x^4(x^4+2)}=\frac{1}{4}\int\frac{\text{d}(x^4+2)}{x^4(x^4+2)}
∫x(x4+2)dx=∫x4(x4+2)x3=41∫x4(x4+2)d(x4+2)
∫
d
x
x
(
1
+
x
7
)
=
∫
x
6
x
7
(
1
+
x
7
)
=
1
7
∫
d
(
x
7
)
x
7
(
1
+
x
7
)
\int\frac{\text{d}x}{x(1+x^7)}=\int\frac{x^6}{x^7(1+x^7)}=\frac{1}{7}\int\frac{\text{d}(x^7)}{x^7(1+x^7)}
∫x(1+x7)dx=∫x7(1+x7)x6=71∫x7(1+x7)d(x7)
(3) 关于
e
x
{\,\color{Blue}e^x\,}
ex:
可以考虑提一项
e
Δ
\,e^\Delta\,
eΔ出来:
∫
d
x
e
x
−
1
=
∫
d
x
e
x
2
1
−
e
−
x
=
−
2
∫
d
(
e
−
x
2
)
1
−
(
e
−
x
2
2
)
2
\int\frac{\text{d}x}{\sqrt{e^x-1}}=\int\frac{\text{d}x}{e^{\frac{x}{2}}\sqrt{1-e^{-x}}}=-2\int\frac{\text{d}(e^{-\frac{x}{2}})}{\sqrt{1-(e^{-\frac{x^2}{2}})^2}}
∫ex−1dx=∫e2x1−e−xdx=−2∫1−(e−2x2)2d(e−2x)
与(1)类似的思路:
(
e
x
±
e
−
x
)
2
=
e
2
x
+
e
−
2
x
±
2
{\color{Purple} (e^x\pm e^{-x})^2=e^{2x}+e^{-2x}\pm 2}\,
(ex±e−x)2=e2x+e−2x±2
∫
e
3
x
+
e
x
e
4
x
+
e
2
x
+
1
d
x
=
∫
e
x
+
e
−
x
e
2
x
+
e
−
2
x
+
1
d
x
\int \frac{e^{3x}+e^x}{e^{4x}+e^{2x}+1}\text{d}x=\int\frac{e^{x}+e^{-x}}{e^{2x}+e^{-2x}+1}\text{d}x
∫e4x+e2x+1e3x+exdx=∫e2x+e−2x+1ex+e−xdx
(4) 连 续 换 元 {\color{Blue}连续换元\,} 连续换元 (换元的基础上再换元)
∫ x sin x cos 3 x d x = − ∫ x d ( cos x ) cos 3 x = 1 2 ∫ x d ( 1 cos 2 x ) \int\frac{x\text{sin}{x}}{\text{cos}^3x}\text{d}x={\color{Purple} -\int\frac{x \text{d}(\text{cos}x)}{\text{cos}^3x}=\frac{1}{2}\int xd\big(\frac{1}{\text{cos}^2x}\big)} ∫cos3xxsinxdx=−∫cos3xxd(cosx)=21∫xd(cos2x1)
第二类换元积分法
使用范围狭窄. 思路与第一类换元积分法正好相反,是将一个 x \,x\, x替换为 t \,t\, t的表达式. 有以下三种使用情形:
(1) 无理函数 ⇒ \,\Rightarrow\, ⇒有理函数
主要是针对处理不了的 f ( x ) \,\sqrt{f(x)} f(x),最后得到 t \,t\, t的积分结果后,直接把 x \,x\, x代回即可.
例:
∫ d x 1 + x = x = t 2 ∫ t 1 + t d t \int\frac{\text{d}x}{1+\sqrt{x}} \xlongequal{\sqrt{x}=t}2\int\frac{t}{1+t}\text{d}t ∫1+xdxx=t2∫1+ttdt ∫ ln ( 1 + x + 1 x ) d x = x + 1 x = t ∫ ln ( 1 + t ) d ( 1 t 2 − 1 ) \int\text{ln}(1+\sqrt{\frac{x+1}{x}})\text{d}x\xlongequal{\sqrt{\frac{x+1}{x}}=t}\int\text{ln}(1+t)\,\text{d}(\frac{1}{t^2-1}) ∫ln(1+xx+1)dxxx+1=t∫ln(1+t)d(t2−11) ∫ d x x + x 3 = x = t 6 6 ∫ t 3 t + 1 d t \int\frac{\text{d}x}{\sqrt{x}+\sqrt[3]{x}}\xlongequal{x=t^6}6\int\frac{t^3}{t+1}\text{d}t ∫x+3xdxx=t66∫t+1t3dt ∫ 1 x 1 + x 1 − x d x = 1 + x 1 − x = t . . . \int\frac{1}{x}\sqrt{\frac{1+x}{1-x}}\text{d}x\xlongequal{\sqrt{\frac{1+x}{1-x}}=t}... ∫x11−x1+xdx1−x1+x=t...
(2) 三角代换
针对被积函数含有处理不了的平方差或平方和. 读者需尤其注意 sec \,\text{sec}\, sec代换必须要分类讨论.
重要手法:
(1) 分子或分母出现 a 2 − x 2 \,\color{Blue}\sqrt{a^2-x^2} a2−x2 ( a > 0 a>0 a>0)
令 x = a ⋅ sin t \,\color{Purple}x=a\cdot\text{sin}t x=a⋅sint, t ∈ ( − π 2 , π 2 ) \color{Purple}t\in(-\frac{\pi}{2},\frac{\pi}{2}) t∈(−2π,2π).
则 t = arcsin x a \,t=\text{arcsin}\frac{x}{a} t=arcsinax, a 2 − x 2 = a ∣ cos t ∣ = a cos t \sqrt{a^2-x^2}=a|{\text{cos}t}|=a\text{cos}t a2−x2=a∣cost∣=acost.
请读者尤其关注三角代换中 t \,t\, t的取值范围. 在正式计算过程中,不可忽略此范围!此范围保证了以下三点:
a ) a) a) 开区间保证 a 2 − x 2 \,\sqrt{a^2-x^2}\, a2−x2出现在分母时不为 0 \,0 0.
b ) b) b) 确保了反三角函数( arcsin \text{arcsin} arcsin)的范围在定义域内: − 1 < x a < 1 -1<\frac{x}{a}<1 −1<ax<1.
c ) c) c) 最终代换的结果无需带绝对值.
(2) 分子或分母出现 x 2 + a 2 \,\color{Blue}\sqrt{x^2+a^2} x2+a2 ( a > 0 a>0 a>0)
令 x = a ⋅ tan t \,\color{Purple}x=a\cdot\text{tan}t x=a⋅tant, t ∈ ( − π 2 , π 2 ) \color{Purple}t\in(-\frac{\pi}{2},\frac{\pi}{2}) t∈(−2π,2π).
则 t = arctan x a \,t=\text{arctan}\frac{x}{a} t=arctanax, x 2 + a 2 = a ∣ sec t ∣ = a sec t \sqrt{x^2+a^2}=a|{\text{sec}t}|=a\text{sec}t x2+a2=a∣sect∣=asect.
t t\, t的范围保证了以下三点:
a ) a) a) 开区间保证 x 2 + a 2 \,\sqrt{x^2+a^2}\, x2+a2出现在分母时不为 0 \,0 0.
b ) b) b) 确保了反三角函数( arctan \text{arctan} arctan)的范围在定义域内: − ∞ < x a < + ∞ -\infty<\frac{x}{a}<+\infty −∞<ax<+∞.
c ) c) c) 最终代换的结果无需带绝对值.
(3) 分子或分母出现 x 2 − a 2 \,\color{Blue}\sqrt{x^2-a^2} x2−a2 ( a > 0 a>0 a>0)
令 x = a ⋅ sec t \,\color{Purple}x=a\cdot\text{sec}t x=a⋅sect, t ∈ ( 0 , π 2 ) ∪ ( π 2 , π ) \color{Purple}t\in(0,\frac{\pi}{2})\cup(\frac{\pi}{2},\pi) t∈(0,2π)∪(2π,π).
则 t = arccos a x \,t=\text{arccos}\frac{a}{x} t=arccosxa, x 2 − a 2 = a ∣ tan t ∣ \sqrt{x^2-a^2}=a{\color{Red}|}{\text{tan}t}{\color{Red}|} x2−a2=a∣tant∣. 此绝对值不可去掉!(除非题目说明 x > a \,x>a x>a)
t t\, t的范围保证了以下两点:
a ) a) a) 开区间保证 x 2 − a 2 \,\sqrt{x^2-a^2}\, x2−a2出现在分母时不为 0 \,0 0.
b ) b) b) 确保了反三角函数( arccos \text{arccos} arccos)的范围在定义域内: − 1 < a x < 1 -1<\frac{a}{x}<1 −1<xa<1.
由于绝对值不可去掉,之后就需要对 t \,t\, t的两段区间进行分类讨论,得到综合的结果.
得到 t \,t\, t的积分结果后,需要通过画三角形分析得到 x = f ( t ) \,x=f(t)\, x=f(t)再代回.
(3) 倒代换
令 x = 1 t 令\,x=\frac{1}{t} 令x=t1
一般遇到分母次数高,分子次数低的情况可以考虑使用倒代换.
∫ d x x 3 x 4 + 1 = x = 1 t ∫ − 1 t 2 1 t 3 ⋅ 1 + 1 t 4 d t = − ∫ t 3 t 4 + 1 d t \int\frac{\text{d}x}{x^3\sqrt{x^4+1}}\xlongequal{x=\frac{1}{t}}\int\frac{-\frac{1}{t^2}}{\frac{1}{t^3}\cdot\sqrt{1+\frac{1}{t^4}}}\text{d}t=-\int\frac{t^3}{\sqrt{t^4+1}}\text{d}t ∫x3x4+1dxx=t1∫t31⋅1+t41−t21dt=−∫t4+1t3dt
(4) 简化高次项
在被积函数最低次是一个高次项时,直接分析可能比较混乱,难以看清套路,可以考虑对其进行整体代换.
∫ x 14 ( x 5 + 1 ) 4 d x = 1 15 ∫ d ( x 15 ) ( x 5 + 1 ) 4 = x 5 = t 1 5 ∫ t 2 ( t + 1 ) 4 dt = 1 5 ∫ ( t + 1 ) 2 − 2 ( t + 1 ) + 1 ( t + 1 ) 4 d t \int\frac{x^{14}}{(x^5+1)^4}\text{d}x=\frac{1}{15}\int\frac{\text{d}(x^{15})}{(x^5+1)^4}\xlongequal{x^5=t}\frac{1}{5}\int\frac{t^2}{(t+1)^4}\text{dt}=\frac{1}{5}\int\frac{(t+1)^2-2(t+1)+1}{(t+1)^4}\text{d}t ∫(x5+1)4x14dx=151∫(x5+1)4d(x15)x5=t51∫(t+1)4t2dt=51∫(t+1)4(t+1)2−2(t+1)+1dt
(二) 分部积分法
∫ u d v = u v − ∫ v d u \int u\text{d}v=uv-\int v\text{d}u ∫udv=uv−∫vdu
一定注意将不能处理的项放在左侧,能处理的项都清理干净全部放在右侧,再使用分部积分法. 强烈建议使用表格法计算这类积分,可大大提升计算速度!
六种基本情况:
(1)
∫
\int\,
∫幂函数
×
\,\times\,
×指数函数
d
x
\,\text{d}x
dx
将指数函数往后移:
∫
x
2
e
x
d
x
=
∫
x
2
d
(
e
x
)
\int x^2e^x\text{d}x=\int{x^2}\text{d}(e^x)
∫x2exdx=∫x2d(ex)
(2)
∫
\int\,
∫幂函数
×
\,\times\,
×对数函数
d
x
\,\text{d}x
dx
将幂函数往后移:
∫
x
ln
2
x
d
x
=
1
2
∫
ln
2
x
d
(
x
2
)
\int x\text{ln}^2x\text{d}x=\frac{1}{2}\int\text{ln}^2x\text{d}({x^2})
∫xln2xdx=21∫ln2xd(x2)
(3)
∫
\int\,
∫幂函数
×
\,\times\,
×三角函数
d
x
\,\text{d}x
dx
将三角函数往后移:
∫
x
2
cos
2
x
d
x
=
1
2
∫
x
2
d
(
sin
2
x
)
\int x^2\text{cos}2x\text{d}x=\frac{1}{2}\int x^2\text{d}(\text{sin}2x)
∫x2cos2xdx=21∫x2d(sin2x)
若三角函数带平方,要先考虑降次.
(4)
∫
\int\,
∫幂函数
×
\,\times\,
×反三角函数
d
x
\,\text{d}x
dx
将幂函数往后移:
∫
x
2
arctan
x
d
x
=
1
3
∫
arctan
x
d
(
x
3
)
\int x^2\text{arctan}x\text{d}x=\frac{1}{3}\int\text{arctan}x\text{d}(x^3)
∫x2arctanxdx=31∫arctanxd(x3)
又比如下面这种直接使用分部积分即可:
∫
arcsin
x
⋅
arccos
x
d
x
\int\text{arc}\text{sin}x\cdot\text{arc}\text{cos}x\text{d}x
∫arcsinx⋅arccosxdx
∫ ( arcsin x ) 2 d x \int(\text{arcsin}x)^2\text{d}x ∫(arcsinx)2dx
(5)
∫
e
a
x
×
{
sin
b
x
cos
b
x
d
x
\int e^{ax}\times\begin{cases}\text{sin}bx\\\text{cos}bx\end{cases}\text{d}x
∫eax×{sinbxcosbxdx
这种情况会出现循环!
要先设
I
=
\,I=\,
I=原式
=
.
.
.
\,=...
=...
(6)
∫
{
sec
n
x
csc
n
x
d
x
\int \begin{cases}\text{sec}^nx\\\text{csc}^nx\end{cases}\text{d}x\,\,
∫{secnxcscnxdx(
n
n\,
n为奇数).
这种情况会出现循环!
要先设
I
n
=
\,I_n=\,
In=原式
=
.
.
.
\,=...
=...
裂出无法求出积分的项:
在使用分部积分法的过程中,可能会裂出无法直接求出积分的项. 应该先不做处理,继续使用分部积分裂出的新项可能将其抵消掉.
特征:通常含有
e
a
x
\,\color{Purple}e^{ax}
eax.
∫ x e x ( x + 1 ) 2 d x = ∫ ( x + 1 ) e x − e x ( x + 1 ) 2 d x \int\frac{xe^x}{(x+1)^2}\text{d}x=\int\frac{(x+1)e^x-e^x}{(x+1)^2}\text{d}x ∫(x+1)2xexdx=∫(x+1)2(x+1)ex−exdx = ∫ e x x + 1 d x − ∫ e x ( x + 1 ) 2 d x ={\color{Blue}\int\frac{e^x}{x+1}\text{d}x}-\int\frac{e^x}{(x+1)^2}\text{d}x =∫x+1exdx−∫(x+1)2exdx = ∫ e x x + 1 d x + ∫ e x d ( 1 x + 1 ) ={\color{Blue}\int\frac{e^x}{x+1}\text{d}x}+\int e^x\text{d}(\frac{1}{x+1}) =∫x+1exdx+∫exd(x+11) = ∫ e x x + 1 d x + e x x + 1 − ∫ e x x + 1 d x = e x x + 1 + C ={\color{Purple}\int\frac{e^x}{x+1}\text{d}x}+\frac{e^x}{x+1}-{\color{Purple}\int\frac{e^x}{x+1}\text{d}x}=\frac{e^x}{x+1}+C =∫x+1exdx+x+1ex−∫x+1exdx=x+1ex+C
推广分布积分公式:
∫ u v ( n + 1 ) d x = u v ( n ) − u ′ v ( n − 1 ) + u ′ ′ v ( n − 2 ) − . . . + ( − 1 ) n u ( n ) v + ( − 1 ) ( n + 1 ) ∫ u ( n + 1 ) v d x \int uv^{(n+1)}\text{d}x=uv^{(n)}-u'v^{(n-1)}+u''v^{(n-2)}-...+(-1)^nu^{(n)}v+(-1)^{(n+1)}\int u^{(n+1)}v\text{d}x ∫uv(n+1)dx=uv(n)−u′v(n−1)+u′′v(n−2)−...+(−1)nu(n)v+(−1)(n+1)∫u(n+1)vdx
3 两类特殊函数的不定积分
(一) 有理函数不定积分
定义:
P
(
x
)
、
Q
(
x
)
P(x)、Q(x)\,
P(x)、Q(x)为多项式:
∫
R
(
x
)
d
x
,
R
(
x
)
=
P
(
x
)
Q
(
x
)
\int R(x)\text{d}x,R(x)=\frac{P(x)}{Q(x)}
∫R(x)dx,R(x)=Q(x)P(x)
If
d
e
g
(
P
)
<
d
e
g
(
Q
)
\text{If}\;\;deg(P)<deg(Q)
Ifdeg(P)<deg(Q),
R
(
x
)
R(x)\,
R(x)为真分式;
If
d
e
g
(
P
)
⩾
d
e
g
(
Q
)
\text{If}\;\;deg(P)\geqslant deg(Q)
Ifdeg(P)⩾deg(Q),
R
(
x
)
R(x)\,
R(x)为假分式;
∫
R
(
x
)
d
x
\int R(x)\text{d}x\,
∫R(x)dx即为有理函数的不定积分.
d e g ( X ) deg(X) deg(X),表示多项式 X \,X\, X的次数.
求解步骤:拆分、求待定系数、求不定积分.
拆分方法
A
.
A.
A.
R
(
x
)
\,R(x)\,
R(x)为假分式:
R
(
x
)
=
多
项
式
+
真
分
式
R(x)=多项式+真分式
R(x)=多项式+真分式
使用凑项、多项式除法等方法进行拆分.
B
.
B.
B.
R
(
x
)
\,R(x)\,
R(x)为真分式:
R
(
x
)
=
分
子
不
变
因
式
分
解
=
(
拆
分
成
的
)
部
分
和
R(x)=\frac{分子不变}{因式分解}=(拆分成的)部分和
R(x)=因式分解分子不变=(拆分成的)部分和
(1) 分母中含
(
x
−
a
)
m
\,(x-a)^m\,
(x−a)m,则分解为:
A
1
x
−
a
+
A
2
(
x
−
a
)
2
+
.
.
.
+
A
m
(
x
−
a
)
m
\frac{A_1}{x-a}+\frac{A_2}{(x-a)^2}+...+\frac{A_m}{(x-a)^m}
x−aA1+(x−a)2A2+...+(x−a)mAm
(2) 分母中含
(
a
x
2
+
b
x
+
c
)
m
\,(ax^2+bx+c)^m\;
(ax2+bx+c)m
(
b
2
−
4
a
c
<
0
(b^2-4ac<0
(b2−4ac<0,即不可因式分解的因子
)
)
),则分解为:
A
1
x
+
B
1
a
x
2
+
b
x
+
c
+
A
2
x
+
B
2
(
a
x
2
+
b
x
+
c
)
2
+
.
.
.
+
A
m
x
+
B
m
(
a
x
2
+
b
x
+
c
)
m
\frac{A_1x+B_1}{ax^2+bx+c}+\frac{A_2x+B_2}{(ax^2+bx+c)^2}+...+\frac{A_mx+B_m}{(ax^2+bx+c)^m}
ax2+bx+cA1x+B1+(ax2+bx+c)2A2x+B2+...+(ax2+bx+c)mAmx+Bm
下面列举一些实例:
case 1:
分母为 ( 2 x + 1 ) ( x − 1 ) \,(2x+1)(x-1) (2x+1)(x−1),拆为:
A 2 x + 1 + B x − 1 \frac{A}{2x+1}+\frac{B}{x-1} 2x+1A+x−1Bcase 2:
分母为 x ( x − 1 ) 2 \,x(x-1)^2 x(x−1)2,拆为:
A x + B x − 1 + C ( x − 1 ) 2 \frac{A}{x}+\frac{B}{x-1}+\frac{C}{(x-1)^2} xA+x−1B+(x−1)2C分母为 ( x + 1 ) 3 \,(x+1)^3 (x+1)3,拆为:
A x + 1 + B ( x + 1 ) 2 + C ( x + 1 ) 3 \frac{A}{x+1}+\frac{B}{(x+1)^2}+\frac{C}{(x+1)^3} x+1A+(x+1)2B+(x+1)3Ccase 3:
分母为 ( 2 x − 1 ) ( x 2 + 1 ) \,(2x-1)(x^2+1) (2x−1)(x2+1),拆为:
A 2 x − 1 + B x + C x 2 + 1 \frac{A}{2x-1}+\frac{Bx+C}{x^2+1} 2x−1A+x2+1Bx+C分母为 ( x − 2 ) ( x 2 + x + 3 ) \,(x-2)(x^2+x+3) (x−2)(x2+x+3),拆为:
A x − 2 + B x + C x 2 + x + 3 \frac{A}{x-2}+\frac{Bx+C}{x^2+x+3} x−2A+x2+x+3Bx+C
复杂因式分解:试根、多项式除法.
如: 1 x 3 − 3 x 2 + 2 \frac{1}{x^3-3x^2+2} x3−3x2+21
(1) 试根,很容易观察到当 x = 1 \,x=1\, x=1时, x 3 − 3 x 2 + 2 = 0 {x^3-3x^2+2}=0 x3−3x2+2=0.
(2) 多项式除法, x 3 − 3 x 2 + 2 {x^3-3x^2+2}\, x3−3x2+2除以 ( x − 1 ) \,(x-1) (x−1),得 x 2 − 2 x − 2 \,x^2-2x-2 x2−2x−2. 于是 x 3 − 3 x 2 + 2 = ( x − 1 ) ( x 2 − 2 x − 2 ) \,{x^3-3x^2+2}=(x-1)(x^2-2x-2) x3−3x2+2=(x−1)(x2−2x−2). 之后可进一步对 ( x 2 − 2 x − 2 ) \,(x^2-2x-2)\, (x2−2x−2)进行因式分解.
求解待定系数的技巧
求解待定系数的通法是列方程组求解,因此计算相对复杂. 对于不同的类型的因子,可以使用以下这些方法快速确定待定系数:
a. 留数法
因子类型: ( x − a ) m (x-a)^m (x−a)m.
思路:
(1) 对于最高次幂:直接使用留数法.
(2) 对于其他次幂:还需要结合其他方法 (两边求导、特殊值法、极限法).
例. 1 ( x − 1 ) ( x − 2 ) ( x − 3 ) \frac{1}{(x-1)(x-2)(x-3)} (x−1)(x−2)(x−3)1
思路:
1 ( x − 1 ) ( x − 2 ) ( x − 3 ) = a x − 1 + b x − 2 + c x − 3 \frac{1}{(x-1)(x-2)(x-3)}=\frac{a}{x-1}+\frac{b}{x-2}+\frac{c}{x-3} (x−1)(x−2)(x−3)1=x−1a+x−2b+x−3c两边同乘 ( x − 1 ) \,(x-1)\, (x−1):
1 ( x − 2 ) ( x − 3 ) = a + ( b x − 2 + c x − 3 ) ( x − 1 ) \frac{1}{(x-2)(x-3)}=a+\bigg(\frac{b}{x-2}+\frac{c}{x-3}\bigg)(x-1) (x−2)(x−3)1=a+(x−2b+x−3c)(x−1)令 x = 1 \,x=1\, x=1, a = 1 2 a=\frac{1}{2} a=21. 同样的方法可以求出 b = − 1 , c = 1 2 \,b=-1,\,c=\frac{1}{2}\, b=−1,c=21
b. 特殊值法
因子类型:
(1)
(
x
−
a
)
m
(x-a)^m
(x−a)m,但
m
\,m\,
m不是最高次幂.
(2)
(
a
x
2
+
b
x
+
c
)
m
\,(ax^2+bx+c)^m\;
(ax2+bx+c)m
(
b
2
−
4
a
c
<
0
)
(b^2-4ac<0)
(b2−4ac<0).
思路:由于不是最高次幂,使用留数法以后会出现代入 x = a \,x=a\, x=a等于无穷的情况,考虑代入其他特殊值:
例. 5 x + 1 ( x + 1 ) 2 \frac{5x+1}{(x+1)^2} (x+1)25x+1
思路:
5 x + 1 ( x + 1 ) 2 = a x + 1 + b ( x + 1 ) 2 ( ∗ ) \frac{5x+1}{(x+1)^2}=\frac{a}{x+1}+\frac{b}{(x+1)^2}\;\;\;(*) (x+1)25x+1=x+1a+(x+1)2b(∗)( ∗ ) (*)\, (∗)式两边同乘 ( x + 1 ) 2 \,(x+1)^2\, (x+1)2:
5 x + 1 = a ( x + 1 ) + b 5x+1=a(x+1)+b 5x+1=a(x+1)+b令 x = − 1 \,x=-1\, x=−1, b = − 4 b=-4 b=−4.
(特殊值法)
( ∗ ) (*)\, (∗)式两边同乘 ( x + 1 ) \,(x+1)\; (x+1)(不是最高次幂):
5 x + 1 x + 1 = a − 4 x + 1 \frac{5x+1}{x+1}=a-\frac{4}{x+1} x+15x+1=a−x+14
此时不能代入 x = − 1 x=-1 x=−1,考虑代入 x = 1 \,x=1 x=1,解得 a = 5 \,a=5 a=5.
c. 极限法
因子类型:
(1)
(
x
−
a
)
m
(x-a)^m
(x−a)m,但
m
\,m\,
m不是最高次幂.
(2)
(
a
x
2
+
b
x
+
c
)
m
\,(ax^2+bx+c)^m\;
(ax2+bx+c)m
(
b
2
−
4
a
c
<
0
)
(b^2-4ac<0)
(b2−4ac<0).
思路:极限法与特殊值法应用场景相同,哪个方便用哪个. 由于不是最高次幂,使用留数法以后会出现代入 x = a \,x=a\, x=a等于无穷的情况,考虑代入其他特殊值:
例. 5 x + 1 ( x + 1 ) 2 \frac{5x+1}{(x+1)^2} (x+1)25x+1
思路:
5 x + 1 ( x + 1 ) 2 = a x + 1 + b ( x + 1 ) 2 ( ∗ ) \frac{5x+1}{(x+1)^2}=\frac{a}{x+1}+\frac{b}{(x+1)^2}\;\;\;(*) (x+1)25x+1=x+1a+(x+1)2b(∗)( ∗ ) (*)\, (∗)式两边同乘 ( x + 1 ) 2 \,(x+1)^2\, (x+1)2:
5 x + 1 = a ( x + 1 ) + b 5x+1=a(x+1)+b 5x+1=a(x+1)+b令 x = − 1 \,x=-1\, x=−1, b = − 4 b=-4 b=−4.
(极限法)
( ∗ ) (*)\, (∗)式两边同乘 ( x + 1 ) \,(x+1)\; (x+1)(不是最高次幂):
5 x + 1 x + 1 = a − 4 x + 1 \frac{5x+1}{x+1}=a-\frac{4}{x+1} x+15x+1=a−x+14
此时不能代入 x = − 1 x=-1 x=−1,考虑令 x → ∞ \,x\to\infty\, x→∞,解得 a = 5 \,a=5 a=5.
(二) 三角函数的不定积分
下面提供一些处理含三角函数的思路:
(1) 积分出现
1
+
cos
x
\;{\color{Blue}1+\text{cos}x}
1+cosx,考虑如下转换:
1
+
cos
x
=
2
cos
2
x
2
{\color{Purple} 1+\text{cos}x=2\text{cos}^2\frac{x}{2} }
1+cosx=2cos22x
∫ d x 1 + cos x = ∫ d x 2 cos 2 x 2 = 1 2 ∫ sec 2 x 2 d x = tan x 2 + C \int\frac{\text{d}x}{1+\text{cos}x}=\int\frac{\text{d}x}{2\text{cos}^2\frac{x}{2}}=\frac{1}{2}\int\text{sec}^2\frac{x}{2}\text{d}x=\text{tan}\frac{x}{2}+C ∫1+cosxdx=∫2cos22xdx=21∫sec22xdx=tan2x+C
(2) 积分出现
1
+
sin
x
\;{\color{Blue}1+\text{sin}x}
1+sinx,可考虑如下三种转换:
1
+
sin
x
=
1
+
cos
(
x
−
π
2
)
{\color{Purple} 1+\text{sin}x=1+\text{cos}(x-\frac{\pi}{2}) }
1+sinx=1+cos(x−2π)
1
+
sin
x
=
sin
2
x
+
cos
2
x
+
2
sin
x
2
cos
x
2
=
(
sin
x
2
+
cos
x
2
)
2
{\color{Purple} 1+\text{sin}x=\text{sin}^2x+\text{cos}^2x+2\,\text{sin}\frac{x}{2}\text{cos}\frac{x}{2}=(\text{sin}\frac{x}{2}+\text{cos}\frac{x}{2})^2}
1+sinx=sin2x+cos2x+2sin2xcos2x=(sin2x+cos2x)2
1
1
+
sin
x
=
1
−
sin
x
cos
2
x
=
sec
2
x
−
tan
x
⋅
sec
x
{\color{Purple} \frac{1}{1+\text{sin}x}=\frac{1-\text{sin}x}{\text{cos}^2x}=\text{sec}^2x-\text{tan}x\cdot\text{sec}x}
1+sinx1=cos2x1−sinx=sec2x−tanx⋅secx
∫ d x 1 + sin x = ∫ d ( x − π 2 ) 1 + cos ( x − π 2 ) = 2 ∫ d ( x 2 − π 4 ) 2 cos 2 ( x 2 − π 4 ) = tan ( x 2 − π 4 ) + C \int\frac{\text{d}x}{1+\text{sin}x}=\int\frac{\text{d}(x-\frac{\pi}{2})}{1+\text{cos}(x-\frac{\pi}{2})}=2\int\frac{\text{d}(\frac{x}{2}-\frac{\pi}{4})}{2\text{cos}^2(\frac{x}{2}-\frac{\pi}{4})}=\text{tan}(\frac{x}{2}-\frac{\pi}{4})+C ∫1+sinxdx=∫1+cos(x−2π)d(x−2π)=2∫2cos2(2x−4π)d(2x−4π)=tan(2x−4π)+C ∫ d x 1 + sin x = ∫ d x ( sin x 2 + cos x 2 ) 2 = ∫ sec 2 x 2 ( 1 + tan x 2 ) 2 d x \int\frac{\text{d}x}{1+\text{sin}x}=\int\frac{\text{d}x}{(\text{sin}\frac{x}{2}+\text{cos}\frac{x}{2})^2}=\int\frac{\text{sec}^2\frac{x}{2}}{(1+\text{tan}\frac{x}{2})^2}\text{d}x ∫1+sinxdx=∫(sin2x+cos2x)2dx=∫(1+tan2x)2sec22xdx ∫ d x 1 + sin x = ∫ 1 − sin x cos 2 x d x = . . . \int\frac{\text{d}x}{1+\text{sin}x}=\int\frac{1-\text{sin}x}{\text{cos}^2x}\text{d}x=... ∫1+sinxdx=∫cos2x1−sinxdx=...
(3) 积分出现
a
sin
x
+
b
cos
x
\,{\color{Blue}a\text{sin}x+b\text{cos}x}
asinx+bcosx,可考虑辅助角公式:
a
sin
x
+
b
cos
x
=
a
2
+
b
2
sin
(
x
+
arctan
b
a
)
(
a
>
0
)
{\color{Purple} a\,\text{sin}x+b\,\text{cos}x=\sqrt{a^2+b^2}\,\text{sin}(x+\text{arctan}\frac{b}{a})\;\;(a>0)}
asinx+bcosx=a2+b2sin(x+arctanab)(a>0)
a
sin
x
+
b
cos
x
=
a
2
+
b
2
cos
(
x
−
arctan
a
b
)
(
b
>
0
)
{\color{Purple} a\,\text{sin}x+b\,\text{cos}x=\sqrt{a^2+b^2}\,\text{cos}(x-\text{arctan}\frac{a}{b})\;\;(b>0)}
asinx+bcosx=a2+b2cos(x−arctanba)(b>0)
∫ d x 2 + sin x + cos x = 1 2 ∫ d x 1 + sin ( x + π 4 ) \int\frac{\text{d}x}{\sqrt{2}+\text{sin}x+\text{cos}x}=\frac{1}{\sqrt{2}}\int\frac{\text{d}x}{1+\text{sin}(x+\frac{\pi}{4})} ∫2+sinx+cosxdx=21∫1+sin(x+4π)dx ∫ 1 cos x − sin x d x = 1 2 ∫ d ( x + π 4 ) cos ( x + π 4 ) \int\frac{1}{\text{cos}{x}-\text{sin}x}\text{d}x=\frac{1}{\sqrt{2}}\int\frac{\text{d}(x+\frac{\pi}{4})}{\text{cos}(x+\frac{\pi}{4})} ∫cosx−sinx1dx=21∫cos(x+4π)d(x+4π)
(4) 积分出现
sin
2
x
\,{\color{Blue}\text{sin}^2x}
sin2x、
cos
2
x
{\color{Blue}\text{cos}^2x}\,
cos2x和
常
数
{\,\color{Blue}常数}\,
常数时,考虑进行如下转换 (此法运用十分广泛):
分
子
分
母
同
除
:
cos
2
x
{\color{Purple} 分子分母同除:\text{cos}^2x}
分子分母同除:cos2x
∫ d x 1 + cos 2 x = ∫ sec 2 x sec 2 x + 1 d x = ∫ d ( tan x ) ( 2 ) 2 + tan 2 x \int\frac{\text{d}x}{1+\text{cos}^2x}=\int\frac{\text{sec}^2x}{\text{sec}^2x+1}\text{d}x=\int\frac{\text{d}(\text{tan}x)}{(\sqrt{2})^2+\text{tan}^2x} ∫1+cos2xdx=∫sec2x+1sec2xdx=∫(2)2+tan2xd(tanx)
(5) 积分出现
sin
x
⋅
cos
x
\,{\color{Blue}\text{sin}x\cdot\text{cos}x}
sinx⋅cosx,进行如下转换:
sin
x
⋅
cos
x
=
1
2
⋅
sin
2
x
{\color{Purple} \text{sin}x\cdot\text{cos}x=\frac{1} {2}\cdot\text{sin}2x}
sinx⋅cosx=21⋅sin2x
(6) 当被积函数可表示为:
a
sin
x
+
b
cos
x
c
sin
x
+
d
cos
x
\,{\color{Blue}\frac{a\,\text{sin}x+b\,\text{cos}x}{c\,\text{sin}x+d\,\text{cos}x}}
csinx+dcosxasinx+bcosx
令 a sin x + b cos x = A ( c sin x + d cos x ) + B ( c sin x + d cos x ) ′ \;\;{\color{Purple} a\,\text{sin}x+b\,\text{cos}x=A(c\,\text{sin}x+d\,\text{cos}x)+B(c\,\text{sin}x+d\,\text{cos}x)' } asinx+bcosx=A(csinx+dcosx)+B(csinx+dcosx)′
例:
∫ d x 1 + 2 tan x = ∫ cos x 2 sin x + cos x d x \int\frac{\text{d}x}{1+2\text{tan}x}=\int\frac{\text{cos}x}{2\text{sin}x+\text{cos}x}\text{d}x ∫1+2tanxdx=∫2sinx+cosxcosxdx 令 cos x = a ( 2 sin x + cos x ) + b ( 2 sin x + cos x ) ′ ⇒ { 2 a − b = 0 a + 2 b = 1 ⇒ a = 1 5 , b = 2 5 \;\text{cos}x=a(2\text{sin}x+\text{cos}x)+b(2\text{sin}x+\text{cos}x)'\Rightarrow\begin{cases}2a-b=0\\a+2b=1\end{cases}\Rightarrow a=\frac{1}{5},b=\frac{2}{5} cosx=a(2sinx+cosx)+b(2sinx+cosx)′⇒{2a−b=0a+2b=1⇒a=51,b=52.
故:
∫ d x 1 + 2 tan x = 1 5 ∫ d x + 2 5 ∫ d ( 2 sin x + cos x ) 2 sin x + cos x = x 5 + 2 5 ln ∣ 2 sin x + cos x ∣ + C \int\frac{\text{d}x}{1+2\text{tan}x}=\frac{1}{5}\int\text{d}x+\frac{2}{5}\int\frac{\text{d}(2\text{sin}x+\text{cos}x)}{2\text{sin}x+\text{cos}x}=\frac{x}{5}+\frac{2}{5}\text{ln}|2\text{sin}x+\text{cos}x|+C ∫1+2tanxdx=51∫dx+52∫2sinx+cosxd(2sinx+cosx)=5x+52ln∣2sinx+cosx∣+C
(7) 被积函数分子为
1
\,{\color{Blue}1}\,
1,分母为
三
角
函
数
乘
积
\,{\color{Blue}三角函数乘积}\,
三角函数乘积时,进行如下转换:
1
=
sin
2
x
+
cos
2
x
{\color{Purple} 1=\text{sin}^2x+\text{cos}^2x }
1=sin2x+cos2x
∫ d x sin x ⋅ sin2 x = 1 2 ∫ d x sin 2 x ⋅ cos x = 1 2 ∫ sin 2 x + cos 2 x sin 2 x ⋅ cos x \int\frac{\text{d}x}{\text{sin}x\cdot\text{sin2}x}=\frac{1}{2}\int\frac{\text{d}x}{\text{sin}^2x\cdot\text{cos}x}=\frac{1}{2}\int\frac{\text{sin}^2x+\text{cos}^2x}{\text{sin}^2x\cdot\text{cos}x} ∫sinx⋅sin2xdx=21∫sin2x⋅cosxdx=21∫sin2x⋅cosxsin2x+cos2x
连用两次 1 = sin 2 x + cos 2 x \,1=\text{sin}^2x+\text{cos}^2x 1=sin2x+cos2x:
∫ d x sin x cos x 4 \int\frac{\text{d}x}{\text{sin}x\text{cos}x^4} ∫sinxcosx4dx
(8) 积分出现
sin
2
x
\,{\color{Blue}\text{sin}^2x}
sin2x、
cos
2
x
{\color{Blue}\text{cos}^2x}\,
cos2x、
sin
2
x
(
或
sin
x
cos
x
)
{\color{Blue}\text{sin}2x\,(或\text{sin}x\text{cos}x)}\,
sin2x(或sinxcosx)时,考虑进行如下转换:
(
sin
2
x
)
′
=
sin
2
x
,
(
cos
2
x
)
′
=
−
sin
2
x
{\color{Purple} (\text{sin}^2x)' = \text{sin}2x,(\text{cos}^2x)' = -\text{sin}2x}
(sin2x)′=sin2x,(cos2x)′=−sin2x
( a sin 2 x + b cos 2 x ) ′ = ( a − b ) sin 2 x (a\,\text{sin}^2x+b\,\text{cos}^2x)'=(a-b)\text{sin}2x (asin2x+bcos2x)′=(a−b)sin2x
∫ sin 2 x d x sin 2 x − 2 cos 2 x : \int\frac{\text{sin}2x\,\text{d}x}{\text{sin}^2x-2\text{cos}^2x}: ∫sin2x−2cos2xsin2xdx: 因为: ( sin 2 x − 2 cos 2 x ) ′ = 3 sin 2 x (\text{sin}^2x-2\text{cos}^2x)'=3\text{sin}^2x (sin2x−2cos2x)′=3sin2x,
∫ sin 2 x d x sin 2 x − 2 cos 2 x = 1 3 ∫ 3 sin 2 x d x sin 2 x − 2 cos 2 x = 1 3 ∫ d ( sin 2 x − 2 cos 2 x ) sin 2 x − 2 cos 2 x \int\frac{\text{sin}2x\,\text{d}x}{\text{sin}^2x-2\text{cos}^2x}=\frac{1}{3}\int\frac{3\text{sin}2x\,\text{d}x}{\text{sin}^2x-2\text{cos}^2x}=\frac{1}{3}\int\frac{\text{d}(\text{sin}^2x-2\text{cos}^2x)}{\text{sin}^2x-2\text{cos}^2x} ∫sin2x−2cos2xsin2xdx=31∫sin2x−2cos2x3sin2xdx=31∫sin2x−2cos2xd(sin2x−2cos2x)
(9) 积分出现
cos
2
x
\,{\color{Blue}\text{cos}2x}
cos2x、
sin
x
cos
x
{\color{Blue} {\text{sin}x\text{cos}x}}\,
sinxcosx时,进行如下转换:
(
sin
x
cos
x
)
′
=
cos
2
x
{\color{Purple} (\text{sin}x\text{cos}x)'=\text{cos}2x}
(sinxcosx)′=cos2x
∫ cos 2 x d x ( 3 + sin x cos x ) 2 : \int\frac{\text{cos}2x\,\text{d}x}{(3+\text{sin}x\text{cos}x)^2}: ∫(3+sinxcosx)2cos2xdx: 因为: ( 3 + sin x cos x ) ′ = cos 2 x (3+\text{sin}x\text{cos}x)'=\text{cos}2x (3+sinxcosx)′=cos2x,
∫ cos 2 x d x ( 3 + sin x cos x ) 2 = ∫ d ( 3 + sin x cos x ) 3 + sin x cos x \int\frac{\text{cos}2x\,\text{d}x}{(3+\text{sin}x\text{cos}x)^2}=\int\frac{\text{d}(3+\text{sin}x\text{cos}x)}{3+\text{sin}x\text{cos}x} ∫(3+sinxcosx)2cos2xdx=∫3+sinxcosxd(3+sinxcosx)
(10) 积分出现积分出现
sin
4
x
+
cos
4
x
\,{\color{Blue}\text{sin}^4x+\text{cos}^4x}\,
sin4x+cos4x时,进行如下转换:
sin
4
x
+
cos
4
x
=
1
−
2
sin
2
x
cos
2
x
{\color{Purple} \text{sin}^4x+\text{cos}^4x=1-2\text{sin}^2x\text{cos}^2x}
sin4x+cos4x=1−2sin2xcos2x
(11) 积分出现
sin
2
x
\,{\color{Blue}\text{sin}^2x}
sin2x、
cos
2
x
{\color{Blue}\text{cos}^2x}\,
cos2x和
tan
x
{\,\color{Blue}\text{tan}x}\,
tanx时,进行如下转换:
sin
2
x
+
cos
2
x
=
cos
2
x
(
tan
x
2
+
1
)
{\color{Purple}\text{sin}^2x+\text{cos}^2x= \text{cos}^2x(\text{tan}x^2+1)}
sin2x+cos2x=cos2x(tanx2+1)
∫ tan x d x a 2 sin 2 x + b 2 cos 2 x = ∫ tan x d x cos 2 x ( a 2 tan 2 x + b 2 ) = ∫ tan x a 2 tan 2 x + b 2 d ( tan x ) ( a b ≠ 0 ) \int\frac{\text{tan}x\text{d}x}{a^2\text{sin}^2x+b^2\text{cos}^2x}=\int\frac{\text{tan}x\text{d}x}{\text{cos}^2x(a^2\text{tan}^2x+b^2)}=\int\frac{\text{tan}x}{a^2\text{tan}^2x+b^2} \text{d}(\text{tan}x)\;\;(ab\neq 0) ∫a2sin2x+b2cos2xtanxdx=∫cos2x(a2tan2x+b2)tanxdx=∫a2tan2x+b2tanxd(tanx)(ab=0)
(12) 万能公式 (应用范围最广,但通常比较耗时,不建议直接使用)
使用条件:被积函数只含三角函数.
令
u
=
tan
x
2
(
−
π
<
x
<
π
)
\;\color{Purple}u=\text{tan}\frac{x}{2}\;(-\pi<x<\pi)
u=tan2x(−π<x<π),
sin
x
=
2
u
1
+
u
2
,
cos
x
=
1
−
u
2
1
+
u
2
,
d
x
=
2
1
+
u
2
d
u
\color{Purple}\text{sin}x=\frac{2u}{1+u^2},\text{cos}x=\frac{1-u^2}{1+u^2},\text{d}x=\frac{2}{1+u^2}\text{d}u
sinx=1+u22u,cosx=1+u21−u2,dx=1+u22du
注意:
a) 建议先进行适当整理,再使用万能公式,可减少计算量 (尽量剩下
sin
x
、
cos
x
、
tan
x
2
\,\text{sin}x、\text{cos}x、\text{tan}\frac{x}{2}
sinx、cosx、tan2x).
b) 如果是关于
x
\,x\,
x的三角函数,设
u
=
tan
x
2
\,u=\text{tan}\frac{x}{2}
u=tan2x. 如果是关于
2
x
\,2x\,
2x的三角函数,设
u
=
tan
x
\,u=\text{tan}x
u=tanx. 如果是关于
4
x
\,4x\,
4x的三角函数,设
u
=
tan
2
x
\,u=\text{tan}2x
u=tan2x…以此类推.
∫ d x sin 2 x + 2 sin x = 1 2 ∫ d(tan x 2 ) sin x = 1 2 ∫ ( 1 u + u ) d u \int\frac{\text{d}x}{\text{sin}2x+2\text{sin}x}=\frac{1}{2}\int{\frac{\text{d(tan}\frac{x}{2}) }{\text{sin}x}}=\frac{1}{2}\int{(\frac{1}{u}+u)\text{d}u} ∫sin2x+2sinxdx=21∫sinxd(tan2x)=21∫(u1+u)du
4 重要结论
1. 连续函数必有原函数,但有原函数的函数不一定连续.
2. 积分一定是连续函数.
3. 有第一类间断点的函数一定没有原函数.
4. 有第二类间断点的函数有可能有原函数,也可能没有原函数.
5. 若
f
(
x
)
\,f(x)\,
f(x)有原函数,则一定有无数个原函数,且任意两个原函数之差为常数.
题型
1 基本概念 (选择题)
2 求不定积分
(一) 换元积分法
(二) 分部积分法
(三) 有理函数不定积分
思路:
参考记忆内容部分的有理函数不定积分.
(四) 三角函数不定积分
思路:
参考记忆内容部分的三角函数不定积分.
(五) 分段有理函数积分
思路:
下面以
∫
e
∣
x
∣
d
x
\int e^{|x|}\text{d}x
∫e∣x∣dx为例:
1
o
1^o\;
1o求出分段函数:
e
∣
x
∣
=
{
e
x
,
x
⩾
0
,
e
−
x
,
x
<
0
,
e^{|x|}=\begin{cases}e^x,&x\geqslant0,\\e^{-x},&x<0,\end{cases}
e∣x∣={ex,e−x,x⩾0,x<0,
2
o
2^o\;
2o分段求出积分,每一段结果后加的常数要分别写为
C
1
,
C
2
,
.
.
.
,
C
n
\,C_1,C_2,...,C_n
C1,C2,...,Cn:
∫
e
∣
x
∣
d
x
=
{
e
x
+
C
1
,
x
⩾
0
,
−
e
−
x
+
C
2
,
x
<
0
,
\int e^{|x|}\text{d}x=\begin{cases}e^x+C_1,&x\geqslant0,\\-e^{-x}+C_2,&x<0,\end{cases}
∫e∣x∣dx={ex+C1,−e−x+C2,x⩾0,x<0,
3
o
3^o\;
3o确定
C
i
\,C_i\,
Ci之间的关系 (因为积分一定是连续函数):
取
C
1
=
C
\,C_1=C
C1=C,由
1
+
C
=
−
1
+
C
2
\,1+C=-1+C_2
1+C=−1+C2,得
C
2
=
C
+
2
\,C_2=C+2
C2=C+2.
∫
e
∣
x
∣
d
x
=
{
e
x
+
C
,
x
⩾
0
,
−
e
−
x
+
C
+
2
,
x
<
0.
\int e^{|x|}\text{d}x=\begin{cases}e^x+C,&x\geqslant0,\\-e^{-x}+C+2,&x<0.\end{cases}
∫e∣x∣dx={ex+C,−e−x+C+2,x⩾0,x<0.
特别注意:如果间断点不止一个(比如出现其中一段的范围是
2
⩽
x
⩽
5
\,2\leqslant x\leqslant 5
2⩽x⩽5,
x
=
2
x=2\,
x=2和
x
=
5
\,x=5\,
x=5都是间断点),且通过按照第
3
o
\,3^o\,
3o步解得的关系不同(
x
=
2
x=2\,
x=2和
x
=
5
\,x=5\,
x=5分别得到两个不同的关系),此时同一个段函数积分后需要再拆成两段!
(六) 综合型不定积分
特征:
综合使用两类换元积分法、分部积分法、有理函数/三角函数不定积分.
3 根据已知条件求不定积分
主要有以下几种题型:
(1) 根据函数关系式解出函数,再求其不定积分
例.
f
(
x
2
−
1
)
=
ln
x
2
x
2
−
2
f(x^2-1)=\text{ln}{\frac{x^2}{x^2-2}}
f(x2−1)=lnx2−2x2,且
f
[
φ
(
x
)
]
=
ln
x
\,f[\varphi(x)]=\text{ln}x
f[φ(x)]=lnx,求
∫
φ
(
x
)
d
x
\int\varphi(x)\text{d}x
∫φ(x)dx.
(2) 函数是一个极限. 先求极限,再求其不定积分.
例.
f
(
x
)
=
lim
t
→
x
(
x
−
1
t
−
1
)
1
x
−
t
f(x)=\lim\limits_{t \to x}\big(\frac{x-1}{t-1}\big)^{\frac{1}{x-t}}
f(x)=t→xlim(t−1x−1)x−t1,求
∫
f
(
x
)
(
x
−
1
)
2
d
x
\,\int\frac{f(x)}{(x-1)^2}\text{d}x
∫(x−1)2f(x)dx.
(3) 通过
F
(
x
)
\,F(x)\,
F(x)求不定积分
Part 2 定积分及其应用
记忆内容
1 基本概念
(一) 定积分的定义
∫ a b f ( x ) d x = lim λ → 0 ∑ i = 1 n f ( ξ i ) Δ x i \int^b_af(x)\text{d}x=\lim\limits_{\lambda\to 0} \sum\limits^{n}_{i=1} f(\xi_i)\Delta x_i ∫abf(x)dx=λ→0limi=1∑nf(ξi)Δxi
注意:
(1)
λ
→
0
⇒
n
→
∞
\lambda\to0\Rightarrow n\to\infty
λ→0⇒n→∞,反之不对.
(2)
lim
λ
→
0
f
(
ξ
i
)
Δ
x
i
\lim\limits_{\lambda\to 0}f(\xi_i)\Delta x_i\,
λ→0limf(ξi)Δxi与
[
a
,
b
]
\,[a,b]\,
[a,b]的分法、
ξ
i
\xi_i\,
ξi的取法都无关.
(3)
f
(
x
)
f(x)\,
f(x)在
[
a
,
b
]
\,[a,b]\,
[a,b]上有界只是可积的必要条件.
(4) 定积分由上下限和函数关系决定,与积分变量无关.
(5) 重要关系 (用于求极限):
lim
n
→
∞
1
n
∑
i
=
1
n
f
(
i
n
)
=
lim
n
→
∞
1
n
∑
i
=
1
n
f
(
i
−
1
n
)
=
∫
0
1
f
(
x
)
d
x
\lim\limits_{n \to \infty} \frac{1}{n} \sum\limits_{i=1}^{n}f\bigg(\frac{i}{n}\bigg)=\lim\limits_{n \to \infty}{\frac{1}{n}\sum\limits_{i=1}^{n}{f\bigg(\frac{i-1}{n}\bigg)}}=\int_{0}^{1}f(x)dx
n→∞limn1i=1∑nf(ni)=n→∞limn1i=1∑nf(ni−1)=∫01f(x)dx
lim
n
→
∞
1
n
∑
i
=
1
k
n
f
(
i
n
)
=
∫
0
k
f
(
x
)
d
x
\lim\limits_{n \to \infty} \frac{1}{n} \sum\limits_{i=1}^{kn}f\bigg(\frac{i}{n}\bigg)=\int_{0}^{k}f(x)dx
n→∞limn1i=1∑knf(ni)=∫0kf(x)dx
lim
n
→
∞
b
−
a
n
∑
i
=
1
n
f
[
a
+
i
n
(
b
−
a
)
]
=
∫
a
b
f
(
x
)
d
x
\lim_{n\to\infty}\frac{b-a}{n}\sum\limits_{i=1}^nf\bigg[a+\frac{i}{n}(b-a)\bigg]=\int^b_af(x)\text{d}x
n→∞limnb−ai=1∑nf[a+ni(b−a)]=∫abf(x)dx
(二) 原函数存在条件
1. 连续函数
f
(
x
)
\,f(x)\,
f(x)必有原函数
F
(
x
)
\,F(x)\,
F(x).
2. 含有第一类间断点、无穷间断点的函数
f
(
x
)
\,f(x)\,
f(x)没有原函数 (可由导数介值定理确定).
从第2点可以看出,原函数可导,其求导后得到的导函数要么连续,要么含有振荡间断点,只能是两种情况之一.
(三) 可积的条件 (定积分的存在性)
满足下列条件之一,
f
(
x
)
f(x)\,
f(x)在
[
a
,
b
]
\,[a,b]\,
[a,b]上可积:
1.
f
(
x
)
∈
C
[
a
,
b
]
f(x)\in C[a,b]
f(x)∈C[a,b].
2.
f
(
x
)
f(x)\,
f(x)有界且在
[
a
,
b
]
\,[a,b]\,
[a,b]上存在有限个间断点 (即不含无穷间断点,可能含有第一类间断点或振荡间断点).
3.
f
(
x
)
f(x)\,
f(x)在
[
a
,
b
]
\,[a,b]\,
[a,b]上单调.
注意:
(1) 可积与存在原函数是不同的概念. 可积,原函数不一定存在;原函数存在,不一定可积,二者没有必然关系.
(2) 可积的必要条件:有界. 以上三个条件都包含了有界.
积不出来的定积分总结:
有的定积分虽然满足可积条件,但无法使用求定积分的方法求解.
∫
a
b
x
2
n
e
±
a
x
2
d
x
(
a
≠
0
,
n
=
0
,
1
,
2
,
.
.
.
)
\int^b_ax^{\color{Red}2n}e^{\pm ax^2}\text{d}x\;\;(a\neq 0,n=0,1,2,...)
∫abx2ne±ax2dx(a=0,n=0,1,2,...)
∫
a
b
e
k
x
d
x
\int^b_ae^{\frac{k}{x}}\text{d}x
∫abexkdx
∫
a
b
e
a
x
x
d
x
(
a
≠
0
)
\int^b_a\frac{e^{ax}}x\text{d}x\;\;(a\neq 0)
∫abxeaxdx(a=0)
∫
a
b
sin
k
x
d
x
,
∫
a
b
cos
k
x
d
x
\int^b_a\text{sin}{\frac{k}{x}}\text{d}x,\int^b_a\text{cos}{\frac{k}{x}}\text{d}x
∫absinxkdx,∫abcosxkdx
∫
a
b
sin
x
x
d
x
,
∫
a
b
cos
x
x
d
x
,
∫
a
b
tan
x
x
d
x
\int^b_a\frac{\text{sin}x}{x}\text{d}x,\int^b_a\frac{\text{cos}x}{x}\text{d}x,\int^b_a\frac{\text{tan}x}{x}\text{d}x
∫abxsinxdx,∫abxcosxdx,∫abxtanxdx
∫
a
b
sin
x
2
d
x
,
∫
a
b
cos
x
2
d
x
,
∫
a
b
tan
x
2
d
x
\int^b_a\text{sin}x^2\text{d}x,\int^b_a\text{cos}x^2\text{d}x,\int^b_a\text{tan}x^2\text{d}x
∫absinx2dx,∫abcosx2dx,∫abtanx2dx
∫
a
b
x
n
ln
x
d
x
(
n
≠
−
1
)
\int^b_a\frac{x^n}{\text{ln}x}\text{d}x\;\;(n\neq-1)
∫ablnxxndx(n=−1)
∫
a
b
ln
x
x
+
a
d
x
(
a
≠
0
)
\int^b_a\frac{\text{ln}x}{x+a}\text{d}x\;\;(a\neq0)
∫abx+alnxdx(a=0)
∫
a
b
1
x
4
+
a
d
x
(
a
≠
0
)
\int^b_a\frac{1}{\sqrt{x^4+a}}\text{d}x\;\;(a\neq 0)
∫abx4+a1dx(a=0)
∫
a
b
x
1
+
x
3
d
x
\int^b_a\frac{x}{\sqrt{1+x^{3}}}\text{d}x
∫ab1+x3xdx
(四) F ( x ) F(x)\, F(x)的性质
若 f ( x ) \,f(x)\, f(x)可积,则有 F ( x ) = ∫ a x f ( t ) d t \,F(x)=\int_a^xf(t)\text{d}t F(x)=∫axf(t)dt:
1.
F
(
x
)
∈
C
[
a
,
b
]
F(x)\in C[a,b]
F(x)∈C[a,b],且:
(1) 若
x
\,x\,
x为
f
(
x
)
\,f(x)\,
f(x)连续点,则
F
(
x
)
\,F(x)\,
F(x)在该点可导.
(2) 若
x
\,x\,
x为
f
(
x
)
\,f(x)\,
f(x)间断点,则
F
(
x
)
\,F(x)\,
F(x)在该点连续但不一定可导.
注意:由于可积条件已经排除无穷间断点,所以这里的间断点可能是第一类间断点或振荡间断点:
被积函数为可去间断点, F ( x ) F(x)\, F(x)在该点可导.
被积函数为跳跃间断点, F ( x ) F(x)\, F(x)在该点不可导. (其左右导数分别等于被积函数这点的左右极限)
被积函数为振荡间断点, F ( x ) F(x)\, F(x)在该点导数可能存在,也可能不存在. 具体来说,如果是有界振荡点,则可导;如果是无界振荡点,则导数不存在(根本不满足可积的条件).
2.
F
(
x
)
F(x)\,
F(x)与
f
(
x
)
\,f(x)\,
f(x)奇偶性关系:
(1) 若
f
(
x
)
\,f(x)\,
f(x)为奇函数,则
F
(
x
)
\,F(x)\,
F(x)一定是偶函数.
(2) 若
f
(
x
)
\,f(x)\,
f(x)为偶函数,则
F
(
x
)
\,F(x)\,
F(x)不一定是奇函数,但
∫
0
x
f
(
t
)
d
t
\,\int^x_0f(t)\text{d}t\,
∫0xf(t)dt一定是奇函数.
3.
F
(
x
)
F(x)\,
F(x)与
f
(
x
)
\,f(x)\,
f(x)周期性关系:
(1) 若
f
(
x
)
\,f(x)\,
f(x)是周期函数,
F
(
x
)
F(x)\,
F(x)不一定是周期函数.
(2) 若
f
(
x
)
\,f(x)\,
f(x)是周期函数且
∫
0
T
f
(
x
)
d
x
=
0
\,\int^T_0f(x)\text{d}x=0\,
∫0Tf(x)dx=0,则
F
(
x
)
\,F(x)\,
F(x)必为是周期函数.
∫ 0 T f ( x ) d x = 0 ⇔ F ( x ) = F ( x + T ) \int^T_0f(x)\text{d}x=0\Leftrightarrow F(x)=F(x+T) ∫0Tf(x)dx=0⇔F(x)=F(x+T)
2 微积分基本定理
(一) 变积分限函数
定理:
f
(
x
)
∈
C
[
a
,
b
]
f(x)\in C[a,b]
f(x)∈C[a,b],
Φ
(
x
)
=
∫
0
x
f
(
t
)
d
t
\Phi(x)=\int^x_0f(t)\text{d}t
Φ(x)=∫0xf(t)dt,则
Φ
′
(
x
)
=
f
(
x
)
\,\Phi'(x)=f(x)
Φ′(x)=f(x).
注意:
(1) 连续函数必然存在原函数:
f
(
x
)
f(x)\,
f(x)连续
⇒
Φ
(
x
)
=
∫
a
x
f
(
t
)
d
t
\,\Rightarrow\Phi(x)=\int^x_af(t)\text{d}t\,
⇒Φ(x)=∫axf(t)dt为
f
(
x
)
\,f(x)\,
f(x)原函数.
(2) d d x ∫ a x f ( t ) d t = f ( x ) \frac{\text{d}}{\text{d}x}\int^x_af(t)\text{d}t=f(x) dxd∫axf(t)dt=f(x)
(3) d d x ∫ a φ ( x ) f ( t ) d t = f [ φ ( x ) ] ⋅ φ ′ ( x ) \frac{\text{d}}{\text{d}x}\int^{\varphi(x)}_af(t)\text{d}t=f[\varphi(x)]\cdot\varphi'(x) dxd∫aφ(x)f(t)dt=f[φ(x)]⋅φ′(x)
(4) d d x ∫ φ 1 ( x ) φ 2 ( x ) f ( t ) d t = f [ φ 2 ( x ) ] ⋅ φ 2 ′ ( x ) − f [ φ 1 ( x ) ] ⋅ φ 1 ′ ( x ) \frac{\text{d}}{\text{d}x}\int^{\varphi_2(x)}_{\varphi_1(x)}f(t)\text{d}t=f[\varphi_2(x)]\cdot\varphi'_2(x)-f[\varphi_1(x)]\cdot\varphi'_1(x) dxd∫φ1(x)φ2(x)f(t)dt=f[φ2(x)]⋅φ2′(x)−f[φ1(x)]⋅φ1′(x)
(5) 使用变积分限函数计算时,必须先将被积函数中的积分限变量清理干净 (通过直接拆、积分限变换两种方式),再求导数:
F ( x ) = ∫ 0 x ( x − t ) f ( t ) d t = x ∫ 0 x f ( t ) d t − ∫ 0 x t f ( t ) d t F(x)=\int^x_0(x-t)f(t)\text{d}t=x\int^x_0f(t)\text{d}t-\int^x_0tf(t)\text{d}t F(x)=∫0x(x−t)f(t)dt=x∫0xf(t)dt−∫0xtf(t)dt F ( x ) = ∫ 0 x f ( x − t ) d t = x − t = u ∫ 0 x f ( u ) d u F(x)=\int^x_0f(x-t)\text{d}t\xlongequal{x-t=u}\int_0^x f(u)\text{d}u F(x)=∫0xf(x−t)dtx−t=u∫0xf(u)du
(6) 有的积分看上去是定积分,实际上也是变积分限函数.
如:
lim x → 0 ∫ − 1 2 e − x 2 t 2 d t − 3 x 2 \lim\limits_{x\to 0}\frac{\int^2_{-1}e^{-x^2t^2}\text{d}t-3}{x^2} x→0limx2∫−12e−x2t2dt−3其中的 ∫ − 1 2 e − x 2 t 2 d t \,\int^2_{-1}e^{-x^2t^2}\text{d}t\, ∫−12e−x2t2dt实际上就是变积分限函数 (用代换清理被积函数中的 x \,x\, x后,会发现积分上下限中都出现 x \,x x)
正因如此,我们可以直接进行下面等价无穷小的替换简化极限求解.
∫ − 1 2 e − x 2 t 2 d t − 3 = ∫ − 1 2 ( e − x 2 t 2 − 1 ) d t ∼ ∫ − 1 2 − x 2 t 2 d t = − 3 x 2 \int^2_{-1}e^{-x^2t^2}\text{d}t-3=\int^2_{-1}(e^{-x^2t^2}-1)\text{d}t\sim\int^2_{-1}-x^2t^2\text{d}t=-3x^2 ∫−12e−x2t2dt−3=∫−12(e−x2t2−1)dt∼∫−12−x2t2dt=−3x2
(二) N . − L . N.-L. N.−L. (牛顿-莱布尼茨公式)
定理:
f
(
x
)
∈
C
[
a
,
b
]
f(x)\in C[a,b]
f(x)∈C[a,b],且
F
(
x
)
\,F(x)\,
F(x)为
f
(
x
)
\,f(x)\,
f(x)的一个原函数,则
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
.
\int^b_af(x)\text{d}x=F(b)-F(a).
∫abf(x)dx=F(b)−F(a).
注意:
(1)
N
.
−
L
.
N.-L.\,
N.−L.的这两种形式也要熟悉:
F
(
b
)
=
F
(
a
)
+
∫
a
b
f
(
x
)
d
x
F(b)=F(a)+\int^b_af(x)\text{d}x
F(b)=F(a)+∫abf(x)dx
f
(
b
)
−
f
(
a
)
=
∫
a
b
f
′
(
x
)
d
x
f(b)-f(a)=\int^b_af'(x)\text{d}x
f(b)−f(a)=∫abf′(x)dx
(2) 导数的定义结合
N
.
−
L
.
\,N.-L.\,
N.−L.要能一眼看出,且能构造:
lim
x
→
a
∫
a
x
f
(
u
)
d
u
x
−
a
=
lim
x
→
a
f
(
x
)
\lim\limits_{x\to a}\frac{\int^x_af(u)\text{d}u}{x-a}=\lim\limits_{x\to a}f(x)
x→alimx−a∫axf(u)du=x→alimf(x)
(3) 使用 N . − L . \,N.-L.\, N.−L.必须保证函数在区间上有定义且连续.
3 定积分的性质
(一) 一般性质
简单性质
∫ a b f ( x ) d x = − ∫ b a f ( x ) d x \int^b_af(x)\text{d}x=-\int_b^af(x)\text{d}x ∫abf(x)dx=−∫baf(x)dx ∫ a a f ( x ) d x = 0 \int_a^af(x)\text{d}x=0 ∫aaf(x)dx=0 ∫ a b [ f ( x ) ± g ( x ) ] d x = ∫ a b f ( x ) d x ± ∫ a b g ( x ) d x \int^b_a[f(x)\pm g(x)]\text{d}x=\int^b_af(x)\text{d}x\pm\int^b_ag(x)\text{d}x ∫ab[f(x)±g(x)]dx=∫abf(x)dx±∫abg(x)dx ∫ a b k f ( x ) d x = k ∫ a b f ( x ) d x \int^b_akf(x)\text{d}x=k\int^b_af(x)\text{d}x ∫abkf(x)dx=k∫abf(x)dx ∫ a b f ( x ) d x = ∫ a c f ( x ) d x + ∫ c b f ( x ) d x \int^b_af(x)\text{d}x=\int^c_af(x)\text{d}x+\int^b_cf(x)\text{d}x ∫abf(x)dx=∫acf(x)dx+∫cbf(x)dx ∫ a b 1 d x = b − a \int^b_a1\text{d}x=b-a ∫ab1dx=b−a f ( x ) ⩾ 0 ( a ⩽ x ⩽ b ) ⇒ ∫ a b f ( x ) d x ⩾ 0 f(x)\geqslant0\;\;(a\leqslant x\leqslant b) \Rightarrow \int^b_af(x)\text{d}x\geqslant0 f(x)⩾0(a⩽x⩽b)⇒∫abf(x)dx⩾0 f ( x ) ⩾ g ( x ) ( a ⩽ x ⩽ b ) ⇒ ∫ a b f ( x ) d x ⩾ ∫ a b g ( x ) d x f(x)\geqslant g(x)\;\;(a\leqslant x\leqslant b) \Rightarrow \int^b_af(x)\text{d}x\geqslant\int^b_ag(x)\text{d}x f(x)⩾g(x)(a⩽x⩽b)⇒∫abf(x)dx⩾∫abg(x)dx
若 f ( x ) ⩾ g ( x ) \,f(x)\geqslant g(x)\, f(x)⩾g(x)且 f ( x ) ≢ g ( x ) \,f(x)\not\equiv g(x) f(x)≡g(x),则必有 ∫ a b f ( x ) d x > ∫ a b g ( x ) d x \,\int^b_af(x)\text{d}x>\int^b_ag(x)\text{d}x ∫abf(x)dx>∫abg(x)dx
∣ ∫ a b f ( x ) d x ∣ ⩽ ∫ a b ∣ f ( x ) ∣ d x \bigg|\int^b_af(x)\text{d}x\bigg|\leqslant\int^b_a\bigg|f(x)\bigg|\text{d}x ∣∣∣∣∫abf(x)dx∣∣∣∣⩽∫ab∣∣∣∣f(x)∣∣∣∣dx m ( b − a ) ⩽ ∫ a b f ( x ) d x ⩽ M ( b − a ) m(b-a)\leqslant \int^b_af(x)\text{d}x\leqslant M(b-a) m(b−a)⩽∫abf(x)dx⩽M(b−a)
积分中值定理
(基本形式)
f
(
x
)
∈
C
[
a
,
b
]
f(x)\in C{[a,b]}
f(x)∈C[a,b],则
∃
ξ
∈
[
a
,
b
]
\,\exist\xi\in{\color{Blue}[}a,b{\color{Blue}]}
∃ξ∈[a,b],使
∫
a
b
f
(
x
)
d
x
=
f
(
ξ
)
(
b
−
a
)
.
\int_a^bf(x)\text{d}x=f(\xi)(b-a).
∫abf(x)dx=f(ξ)(b−a).
(推广积分中值定理)
f
(
x
)
∈
C
[
a
,
b
]
f(x)\in C[a,b]
f(x)∈C[a,b],则
∃
ξ
∈
(
a
,
b
)
\,\exist\xi\in{\color{Blue}(}a,b{\color{Blue})}
∃ξ∈(a,b),使
∫
a
b
f
(
x
)
d
x
=
f
(
ξ
)
(
b
−
a
)
.
\int_a^bf(x)\text{d}x=f(\xi)(b-a).
∫abf(x)dx=f(ξ)(b−a).
(积分第一中值定理)
f
(
x
)
∈
C
[
a
,
b
]
f(x)\in C[a,b]
f(x)∈C[a,b],
g
(
x
)
g(x)\,
g(x)在
[
a
,
b
]
\,[a,b]\,
[a,b]上可积且不变号,则
∃
ξ
∈
[
a
,
b
]
\,\exist\xi\in{\color{Blue}[}a,b{\color{Blue}]}
∃ξ∈[a,b],使
∫
a
b
f
(
x
)
g
(
x
)
d
x
=
f
(
ξ
)
∫
a
b
g
(
x
)
d
x
.
\int_a^bf(x)g(x)\text{d}x=f(\xi)\int_a^bg(x)\text{d}x.
∫abf(x)g(x)dx=f(ξ)∫abg(x)dx.
变号的出去,不变号的留下!
(推广积分第一中值定理)
f
(
x
)
∈
C
[
a
,
b
]
f(x)\in C[a,b]
f(x)∈C[a,b],
g
(
x
)
g(x)\,
g(x)在
[
a
,
b
]
\,[a,b]\,
[a,b]上可积且不变号,则
∃
ξ
∈
(
a
,
b
)
\,\exist\xi\in{\color{Blue}(}a,b{\color{Blue})}
∃ξ∈(a,b),使
∫
a
b
f
(
x
)
g
(
x
)
d
x
=
f
(
ξ
)
∫
a
b
g
(
x
)
d
x
.
\int_a^bf(x)g(x)\text{d}x=f(\xi)\int_a^bg(x)\text{d}x.
∫abf(x)g(x)dx=f(ξ)∫abg(x)dx.
强烈建议读者掌握几种积分中值定理的证明过程. 证明基本形式和积分第一中值定理需要用到介值定理,证明两种推广积分中值定理则是使用中值定理 (推广积分中值定理使用 L \,\text{L}\, L证明,推广积分第一中值定理使用 C \,\text{C}\, C证明).
注意:
(1) 在定积分相关证明题目的条件中,若出现定积分的积分区间长度与其系数成倒数关系,应该第一时间考虑使用积分中值定理.
(2) 注意积分中值定理基本形式和积分第一中值定理针对闭区间;推广积分中值定理和推广积分第一中值定理则是针对开区间.
判断定积分大小
case1:
{
f
(
x
)
∈
C
[
a
,
b
]
f
(
x
)
⩾
0
∫
a
b
f
(
x
)
d
x
=
0
⇒
f
(
x
)
≡
0
(
a
⩽
x
⩽
b
)
\begin{cases}f(x)\in C[a,b]\\f(x)\geqslant0\\\int^b_af(x)\text{d}x=0\end{cases}\Rightarrow f(x)\equiv 0\;\;(a\leqslant x\leqslant b)
⎩⎪⎨⎪⎧f(x)∈C[a,b]f(x)⩾0∫abf(x)dx=0⇒f(x)≡0(a⩽x⩽b)
case2:
{
f
(
x
)
∈
C
[
a
,
b
]
f
(
x
)
⩾
0
f
(
x
)
≢
0
⇒
∫
a
b
f
(
x
)
d
x
>
0
\begin{cases}f(x)\in C[a,b]\\f(x)\geqslant0\\f(x)\not\equiv0\end{cases}\Rightarrow \int_a^b f(x)\text{d}x > 0
⎩⎪⎨⎪⎧f(x)∈C[a,b]f(x)⩾0f(x)≡0⇒∫abf(x)dx>0
case3:
{
f
(
x
)
、
g
(
x
)
∈
C
[
a
,
b
]
f
(
x
)
⩾
g
(
x
)
f
(
x
)
≢
g
(
x
)
⇒
∫
a
b
f
(
x
)
d
x
>
∫
a
b
g
(
x
)
d
x
\begin{cases}f(x)、g(x)\in C[a,b]\\f(x)\geqslant g(x)\\f(x)\not\equivg(x)\end{cases}\Rightarrow \int_a^b f(x)\text{d}x > \int_a^b g(x)\text{d}x
⎩⎪⎨⎪⎧f(x)、g(x)∈C[a,b]f(x)⩾g(x)f(x)≡g(x)⇒∫abf(x)dx>∫abg(x)dx
柯西不等式
f
(
x
)
、
g
(
x
)
∈
C
[
a
,
b
]
f(x)、g(x)\in C[a,b]
f(x)、g(x)∈C[a,b],则
[
∫
a
b
f
(
x
)
g
(
x
)
d
x
]
2
⩽
∫
a
b
f
2
(
x
)
d
x
⋅
∫
a
b
g
2
(
x
)
d
x
\bigg[\int^b_af(x)g(x)\text{d}x\bigg]^2\leqslant \int_a^b f^2(x)\text{d}x\cdot\int_a^b g^2(x)\text{d}x
[∫abf(x)g(x)dx]2⩽∫abf2(x)dx⋅∫abg2(x)dx
记忆口诀:积的平方小于等于平方的积.
附 (柯西不等式一般形式):
∑ i = 1 n a i 2 ⋅ ∑ i = 1 n b i 2 ⩾ ( ∑ i = 1 n a i b i ) 2 \sum\limits^{n}_{i=1}a_i^2\cdot\sum\limits^{n}_{i=1}b_i^2\geqslant\bigg(\sum\limits^{n}_{i=1}{a_ib_i}\bigg)^2 i=1∑nai2⋅i=1∑nbi2⩾(i=1∑naibi)2
等号成立条件为: a 1 b 1 = a 2 b 2 = . . . = a n b n \frac{a_1}{b_1}=\frac{a_2}{b_2}=...=\frac{a_n}{b_n} b1a1=b2a2=...=bnan,或 a i \,a_i ai、 b i ( i = 1 , 2 , . . . , n ) b_i\;(i=1,2,...,n)\, bi(i=1,2,...,n)中至少有一方全为 0 \,0 0.
(二) 特殊性质
对称区间的定积分性质
f
(
x
)
∈
C
[
−
a
,
a
]
f(x)\in C[-a,a]
f(x)∈C[−a,a],则
∫
−
a
a
f
(
x
)
d
x
=
∫
0
a
[
f
(
x
)
+
f
(
−
x
)
]
d
x
.
\int^a_{-a}f(x)\text{d}x=\int^a_0[f(x)+f(-x)]\text{d}x.
∫−aaf(x)dx=∫0a[f(x)+f(−x)]dx.
特别地,
(1) 若 f ( x ) = − f ( − x ) \,f(x)=-f(-x) f(x)=−f(−x),则 ∫ − a a f ( x ) d x = 0 \,\int_{-a}^af(x)\text{d}x=0 ∫−aaf(x)dx=0;
(2) 若 f ( x ) = f ( − x ) \,f(x)=f(-x) f(x)=f(−x),则 ∫ − a a f ( x ) d x = 2 ∫ 0 a f ( x ) d x \,\int_{-a}^af(x)\text{d}x=2\int_0^af(x)\text{d}x ∫−aaf(x)dx=2∫0af(x)dx.
三角函数的定积分性质
(1)
sin
x
\text{sin}x\,
sinx与
cos
x
\,\text{cos}x\,
cosx互换性质
f
(
x
)
∈
C
[
0
,
1
]
f(x)\in C[0,1]
f(x)∈C[0,1],则
∫
0
π
2
f
(
sin
x
)
d
x
=
∫
0
π
2
f
(
cos
x
)
d
x
.
\,\int_0^{\frac{\pi}{2}}f(\text{sin}x)\text{d}x=\int^{\frac{\pi}{2}}_0f(\text{cos}x)\text{d}x.
∫02πf(sinx)dx=∫02πf(cosx)dx.
∫ 0 π 2 lnsin x d x = ∫ 0 π 2 lncos x d x \int^\frac{\pi}{2}_0\text{ln}\text{sin}x\text{d}x=\int^{\frac{\pi}{2}}_0\text{ln}\text{cos}x\text{d}x ∫02πlnsinxdx=∫02πlncosxdx
特别地, I n = ∫ 0 π 2 sin n x d x = ∫ 0 π 2 cos n x d x I_n=\int_0^{\frac{\pi}{2}}\text{sin}^nx\text{d}x=\int_0^{\frac{\pi}{2}}\text{cos}^nx\text{d}x In=∫02πsinnxdx=∫02πcosnxdx,且 { I n = n − 1 n I n − 2 I 0 = π 2 I 1 = 1 \,\begin{cases}I_n=\frac{n-1}{n}I_{n-2}\\I_0=\frac{\pi}{2}\\I_1=1\end{cases} ⎩⎪⎨⎪⎧In=nn−1In−2I0=2πI1=1
计算举例:
∫ 0 π 2 sin 4 x d x = 3 4 ⋅ 1 2 ⋅ π 2 = 3 π 16 \int^\frac{\pi}{2}_0\text{sin}^4{x}\text{d}x=\frac{3}{4}\cdot\frac{1}{2}\cdot\frac{\pi}{2}=\frac{3\pi}{16} ∫02πsin4xdx=43⋅21⋅2π=163π ∫ 0 π 2 sin 5 x d x = 4 5 ⋅ 2 3 ⋅ 1 = 8 15 \int^\frac{\pi}{2}_0\text{sin}^5{x}\text{d}x=\frac{4}{5}\cdot\frac{2}{3}\cdot 1=\frac{8}{15} ∫02πsin5xdx=54⋅32⋅1=158
(2) 2倍性质
对于
sin
x
\,\text{sin}x
sinx:
∫
0
π
f
(
sin
x
)
d
x
=
2
∫
0
π
2
f
(
sin
x
)
d
x
\int_0^{\pi}f(\text{sin}x)\text{d}x=2\int_0^{\frac{\pi}{2}}f(\text{sin}x)\text{d}x
∫0πf(sinx)dx=2∫02πf(sinx)dx
∫
0
π
2
f
(
sin
x
)
d
x
=
∫
π
2
π
f
(
sin
x
)
d
x
\int_0^{\frac{\pi}{2}}f(\text{sin}x)\text{d}x=\int_{\frac{\pi}{2}}^{\pi}f(\text{sin}x)\text{d}x
∫02πf(sinx)dx=∫2ππf(sinx)dx
特别地,
∫
0
π
sin
n
x
d
x
=
2
∫
0
π
2
sin
n
x
d
x
=
2
I
n
\int_0^{\pi}\text{sin}^nx\text{d}x=2\int_0^{\frac{\pi}{2}}\text{sin}^nx\text{d}x=2I_n
∫0πsinnxdx=2∫02πsinnxdx=2In
对于
cos
x
\,\text{cos}x
cosx:
∫
0
π
f
(
∣
cos
x
∣
)
d
x
=
2
∫
0
π
2
f
(
cos
x
)
d
x
\int_0^{\pi}f(|\text{cos}x|)\text{d}x=2\int_0^{\frac{\pi}{2}}f(\text{cos}x)\text{d}x
∫0πf(∣cosx∣)dx=2∫02πf(cosx)dx
特别地,
∫
0
π
cos
n
x
d
x
=
{
2
∫
0
π
2
cos
n
x
d
x
=
2
I
n
,
n
=
2
,
4
,
6
,
.
.
.
0
,
n
=
1
,
3
,
5
,
.
.
.
\int_0^{\pi}\text{cos}^nx\text{d}x=\begin{cases}2\int_0^{\frac{\pi}{2}}\text{cos}^nx\text{d}x=2I_n,\;\;\;n=2,4,6,...\\0,\;\;\;n=1,3,5,...\end{cases}
∫0πcosnxdx={2∫02πcosnxdx=2In,n=2,4,6,...0,n=1,3,5,...
(3) 消
x
\,x\,
x性质
f
(
x
)
∈
C
[
0
,
1
]
f(x)\in C[0,1]
f(x)∈C[0,1],则
∫
0
π
x
f
(
sin
x
)
d
x
=
π
2
∫
0
π
f
(
sin
x
)
d
x
=
π
∫
0
π
2
f
(
sin
x
)
d
x
\int_0^\pi xf(\text{sin}x)\text{d}x=\frac{\pi}{2}\int^\pi_0f(\text{sin}x)\text{d}x=\pi\int^{\frac{\pi}{2}}_0f(\text{sin}x)\text{d}x
∫0πxf(sinx)dx=2π∫0πf(sinx)dx=π∫02πf(sinx)dx
注意:式中出现 cos x \,\text{cos}{x}\, cosx:只要 cos x \,\text{cos}{x}\, cosx带绝对值或为偶次项,则上面的性质同样满足.
(4) 2
π
\pi\,
π绝对值性质
∫
0
2
π
f
(
∣
sin
x
∣
)
d
x
=
4
∫
0
π
2
f
(
sin
x
)
d
x
\int^{2\pi}_0f(|\text{sin}x|)\text{d}x=4\int^{\frac{\pi}{2}}_0f(\text{sin}x)\text{d}x
∫02πf(∣sinx∣)dx=4∫02πf(sinx)dx
∫
0
2
π
f
(
∣
cos
x
∣
)
d
x
=
4
∫
0
π
2
f
(
cos
x
)
d
x
\int^{2\pi}_0f(|\text{cos}x|)\text{d}x=4\int^{\frac{\pi}{2}}_0f(\text{cos}x)\text{d}x
∫02πf(∣cosx∣)dx=4∫02πf(cosx)dx
周期函数定积分性质
设 f ( x ) \,f(x)\, f(x)是以 T \,T\, T为周期的连续函数,则
(1) 平移性质
∫
a
a
+
T
f
(
x
)
d
x
=
∫
0
T
f
(
x
)
d
x
\int^{a+T}_af(x)\text{d}x=\int^T_0f(x)\text{d}x
∫aa+Tf(x)dx=∫0Tf(x)dx
注意:平移位置根据需求任意选择.
(2) n倍性质
∫
a
n
T
f
(
x
)
d
x
=
n
∫
0
T
f
(
x
)
d
x
\int^{nT}_af(x)\text{d}x=n\int^T_0f(x)\text{d}x
∫anTf(x)dx=n∫0Tf(x)dx
4 积分区间变换技巧
(1) 最简单的变换:
∫
−
a
0
f
(
x
)
d
x
=
x
=
−
t
∫
a
0
f
(
−
t
)
d
(
−
t
)
=
∫
0
a
f
(
−
t
)
d
t
\int^0_{-a}f(x)\text{d}x\xlongequal{\color{Blue}x=-t}\int^0_{a}f(-t)\text{d}(-t)=\int^a_0f(-t)\text{d}t
∫−a0f(x)dxx=−t∫a0f(−t)d(−t)=∫0af(−t)dt
(2) 证明定积分相等,且定积分区间相同:
∫
a
b
f
(
x
)
d
x
=
x
+
t
=
a
+
b
∫
b
a
f
(
a
+
b
−
t
)
d
(
a
+
b
−
t
)
=
∫
a
b
f
(
a
+
b
−
t
)
d
t
\int^b_{a}f(x)\text{d}x\xlongequal{\color{Blue}x+t=a+b}\int^a_bf(a+b-t)\text{d}(a+b-t)=\int^b_af(a+b-t)\text{d}t
∫abf(x)dxx+t=a+b∫baf(a+b−t)d(a+b−t)=∫abf(a+b−t)dt
(3) 0-1变换,证明定积分相等,且另一个定积分积分区间是
[
0
,
1
]
\,[0,1]
[0,1]:
∫
a
b
f
(
x
)
d
x
=
x
=
a
+
(
b
−
a
)
t
(
b
−
a
)
∫
0
1
f
[
a
+
(
b
−
a
)
t
]
d
t
\int^b_af(x)\text{d}x\xlongequal{\color{Blue}x=a+(b-a)t}(b-a)\int^1_0f[a+(b-a)t]\text{d}t
∫abf(x)dxx=a+(b−a)t(b−a)∫01f[a+(b−a)t]dt
(4) 三角函数变换:
π
\pi\,
π型:通过该变换,可实现区间的平移,方便使用特殊性质. 可证明
∫
0
π
x
f
(
sin
x
)
d
x
\,\int^{\pi}_0xf(\text{sin}x)\text{d}x\,
∫0πxf(sinx)dx的特殊性质:
∫
π
2
3
π
2
f
(
cos
x
)
d
x
=
x
−
π
=
t
∫
−
π
2
π
2
f
(
cos
t
)
d
t
=
2
∫
0
π
2
f
(
cos
t
)
d
t
\int_{\frac{\pi}{2}}^{\frac{3\pi}{2}}f(\text{cos}x)\text{d}x\xlongequal{x-{\color{Blue}\pi}=t}\int^{\frac{\pi}{2}}_{-\frac{\pi}{2}}f(\text{cos}t)\text{d}t=2\int^{\frac{\pi}{2}}_0f(\text{cos}t)\text{d}t
∫2π23πf(cosx)dxx−π=t∫−2π2πf(cost)dt=2∫02πf(cost)dt
π
2
\frac{\pi}{2}\,
2π型:通过该变换,可实现被积函数中
sin
x
\,\text{sin}x\,
sinx与
cos
x
\,\text{cos}x\,
cosx、
tan
x
\,\text{tan}x\,
tanx与
cot
x
\,\text{cot}x\,
cotx的转换:
∫
0
π
f
(
cos
x
)
d
x
=
x
=
π
2
−
t
∫
π
2
−
π
2
f
(
sin
t
)
(
−
d
t
)
=
∫
−
π
2
π
2
f
(
sin
t
)
d
t
\int_0^{\pi}f(\text{cos}x)\text{d}x\xlongequal{x={\color{Blue}\frac{\pi}{2}}-t}\int^{-\frac{\pi}{2}}_{\frac{\pi}{2}}f(\text{sin}t)(-\text{d}t)=\int^{\frac{\pi}{2}}_{-\frac{\pi}{2}}f(\text{sin}t)\text{d}t
∫0πf(cosx)dxx=2π−t∫2π−2πf(sint)(−dt)=∫−2π2πf(sint)dt
5 定积分的积分方法
(一) 换元积分法
与不定积分一致.
注意:
(1) 特别强调下面这种基本构造手法,应当非常熟练:
∫
0
2
x
2
2
x
−
x
2
d
x
=
∫
0
2
[
(
x
−
1
)
+
1
]
2
1
−
(
x
−
1
)
2
d
(
x
−
1
)
\int^2_0x^2\sqrt{2x-x^2}\text{d}x=\int^2_0[(x-1)+1]^2\sqrt{1-(x-1)^2}\text{d}(x-1)
∫02x22x−x2dx=∫02[(x−1)+1]21−(x−1)2d(x−1)
∫
0
1
x
arctan
(
x
−
1
)
2
d
x
=
∫
0
1
(
x
−
1
)
arctan
(
x
−
1
)
2
d
(
x
−
1
)
+
∫
0
1
arctan
(
x
−
1
)
2
d
(
x
−
1
)
\int^1_0x\text{arctan}(x-1)^2\text{d}x=\int^1_0(x-1)\text{arctan}(x-1)^2\text{d}(x-1)+\int^1_0\text{arctan}(x-1)^2\text{d}(x-1)
∫01xarctan(x−1)2dx=∫01(x−1)arctan(x−1)2d(x−1)+∫01arctan(x−1)2d(x−1)
(2) 同不定积分,当分母次数高,分子次数低(通常为1)时,要考虑倒代换.
(二) 分部积分法
与不定积分一致.
(三) 根据几何意义
定积分的几何意义:定积分等于被积函数与坐标轴围成的面积,x轴之上部分为正,x轴之下部分为负.
尤其是圆相关的积分,直接看圆的面积计算更快 (可以避免三角代换),如: ∫ 0 2 2 x − x 2 d x \int^2_0\sqrt{2x-x^2}\text{d}x ∫022x−x2dx
y = 2 x − x 2 y=\sqrt{2x-x^2}\, y=2x−x2围成面积为一个半径为 1 \,1\, 1的半圆,所以 ∫ 0 2 2 x − x 2 d x = π 2 \,\int^2_0\sqrt{2x-x^2}\text{d}x=\frac{\pi}{2} ∫022x−x2dx=2π.
(四) 区间再现公式
∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x \int^b_af(x)\text{d}x=\int^b_af(a+b-x)\text{d}x ∫abf(x)dx=∫abf(a+b−x)dx
6 其他重要技巧
(1) 分母有理化
分母有理化在积分中依然有用武之地:
∫
−
1
1
x
x
+
x
2
+
1
d
x
=
∫
−
1
1
x
(
x
2
+
1
−
x
)
(
x
2
+
1
+
x
)
(
x
2
+
1
−
x
)
d
x
\int^{1}_{-1}\frac{x}{x+\sqrt{x^2+1}}\text{d}x=\int^1_{-1}\frac{x(\sqrt{x^2+1}-x)}{(\sqrt{x^2+1}+x)(\sqrt{x^2+1}-x)}\text{d}x
∫−11x+x2+1xdx=∫−11(x2+1+x)(x2+1−x)x(x2+1−x)dx
(2) 拆积分限
极其重要的手法,一旦定积分出现
n
\,n\,
n、出现
Σ
\,\Sigma\,
Σ都要考虑是否需要拆.
拆开以后逐段考虑.
∫
0
n
π
x
∣
cos
x
∣
d
x
=
∫
0
π
x
∣
cos
x
∣
d
x
+
∫
π
2
π
∣
cos
x
∣
d
x
+
.
.
.
+
∫
(
n
−
1
)
π
n
π
∣
cos
x
∣
d
x
\int^{n\pi}_0x|\text{cos}x|\text{d}x=\int^\pi_0x|\text{cos}x|\text{d}x+\int_\pi^{2\pi}|\text{cos}x|\text{d}x+...+\int_{(n-1)\pi}^{n\pi}|\text{cos}x|\text{d}x
∫0nπx∣cosx∣dx=∫0πx∣cosx∣dx+∫π2π∣cosx∣dx+...+∫(n−1)πnπ∣cosx∣dx
∫
0
a
f
(
x
)
d
x
−
a
∫
0
1
f
(
x
)
d
x
=
(
1
−
a
)
∫
0
a
f
(
x
)
d
x
−
a
∫
a
1
f
(
x
)
d
x
\int^a_0f(x)\text{d}x-a\int^1_0f(x)\text{d}x=(1-a)\int^a_0f(x)\text{d}x-a\int^1_af(x)\text{d}x
∫0af(x)dx−a∫01f(x)dx=(1−a)∫0af(x)dx−a∫a1f(x)dx
(3) 定积分+非定积分
一个式子出现一项是定积分,另一项不含定积分,有以下两种处理思路:
(1) 都化为定积分:
∫
a
x
f
(
t
)
d
t
−
(
x
−
a
)
f
(
a
)
=
∫
a
x
f
(
t
)
d
t
−
∫
a
x
f
(
a
)
d
t
=
∫
a
x
[
f
(
t
)
−
f
(
a
)
]
d
t
\int^x_af(t)\text{d}t-(x-a)f(a)=\int^x_af(t)\text{d}t-\int^x_af(a)\text{d}t=\int^x_a\big[f(t)-f(a)\big]\text{d}t
∫axf(t)dt−(x−a)f(a)=∫axf(t)dt−∫axf(a)dt=∫ax[f(t)−f(a)]dt
(2) 都化为不含定积分的项 (积分中值定理):
1
b
−
a
∫
a
b
f
(
x
)
d
x
−
f
(
c
)
=
f
(
ξ
)
−
f
(
c
)
,
ξ
∈
[
a
,
b
]
\frac{1}{b-a}\int^b_af(x)\text{d}x-f(c)=f(\xi)-f(c),\xi\in[a,b]
b−a1∫abf(x)dx−f(c)=f(ξ)−f(c),ξ∈[a,b]
(4) 证明定积分遇到绝对值
应当条件反射:
∣
∫
a
b
f
(
x
)
d
x
∣
⩽
∫
a
b
∣
f
(
x
)
∣
d
x
\bigg|\int^b_af(x)\text{d}x\bigg|\leqslant\int^b_a\big|f(x)\big|\text{d}x
∣∣∣∣∫abf(x)dx∣∣∣∣⩽∫ab∣∣f(x)∣∣dx
(5) 积分过程发现与原式相同的项
立即设 I = \,\text{I}=\, I=原式,然后移项求解.
(6) 周期函数相关总结
1. 三角函数周期 (只讨论
sin
x
\,\text{sin}x\,
sinx和
cos
x
\,\text{cos}x\,
cosx) 的性质:
(1)
sin
n
x
\text{sin}^nx\,
sinnx或
cos
n
x
\,\text{cos}^nx\,
cosnx的周期:
当
n
\,n\,
n为奇数时,周期为
2
π
\,2π
2π;
当
n
\,n\,
n为偶数时,周期为
π
\,π
π.
(2)
sin
ω
x
\text{sin}\omega x
sinωx、
cos
ω
x
\text{cos}\omega x
cosωx的周期为
2
π
ω
\,\frac{2\pi}{\omega}
ω2π.
(3) 一次正余弦加绝对值周期减半:
∣
sin
ω
x
∣
|\text{sin}\omega x|
∣sinωx∣、
∣
cos
ω
x
∣
|\text{cos}\omega x|
∣cosωx∣的周期为
π
ω
\frac{\pi}{\omega}
ωπ.
(4) 有的时候周期不是那么显而易见,但是熟悉周期函数的性质 (
f
(
x
)
=
f
(
x
+
T
)
f(x)=f(x+T)
f(x)=f(x+T))也能很容易看出,如:
f
(
x
)
=
e
sin
x
f(x)=e^{\text{sin}x}
f(x)=esinx,
f
(
x
+
2
π
)
=
e
sin
(
x
+
2
π
)
=
e
sin
x
f(x+2\pi)=e^{\text{sin}(x+2\pi)}=e^{\text{sin}x}
f(x+2π)=esin(x+2π)=esinx,周期还是
2
π
\,2\pi
2π,
可见
e
\,e\,
e的三角函数次幂的周期性等于三角函数的周期;
f
(
x
)
=
sin
2
x
−
sin
4
x
f(x)=\sqrt{\text{sin}^2x-\text{sin}^4x}
f(x)=sin2x−sin4x,显然
sin
2
x
\,\text{sin}^2x\,
sin2x与
sin
4
x
\,\text{sin}^4x\,
sin4x周期都是
π
\,\pi\,
π,根据
f
(
x
)
=
f
(
x
+
π
)
\,f(x)=f(x+\pi)
f(x)=f(x+π),周期还是
π
\,\pi\,
π,
可见一个由三角函数构成的多项式,只要其中每一项的周期都一致,那么开根号不会影响周期.
2. 解答题中经常使用的结论:
对
∀
x
\;\forall\,x
∀x,都存在非负整数
n
\,n\,
n,使得
n
T
⩽
x
⩽
(
n
+
1
)
T
\,\color{Blue}nT\leqslant x\leqslant(n+1)T
nT⩽x⩽(n+1)T.
尤其是题目出现下面这种极限,多半就要使用上面的结论并运用夹逼定理求解:
lim
x
→
+
∞
∫
0
x
f
(
t
)
d
t
x
\lim\limits_{x\to+\infty}{\frac{\int_0^xf(t)\text{d}t}{x}}
x→+∞limx∫0xf(t)dt
若周期函数
f
(
x
)
⩾
0
f(x)\geqslant0
f(x)⩾0,
n
∫
0
T
f
(
x
)
d
x
⩽
∫
0
x
f
(
x
)
d
x
⩽
(
n
+
1
)
∫
0
T
f
(
x
)
d
x
n\int^{T}_0f(x)\text{d}x\leqslant\int^x_0f(x)\text{d}x\leqslant(n+1)\int^{T}_0f(x)\text{d}x
n∫0Tf(x)dx⩽∫0xf(x)dx⩽(n+1)∫0Tf(x)dx
若
f
(
x
)
⩽
0
f(x)\leqslant0
f(x)⩽0,
n
∫
0
T
f
(
x
)
d
x
⩾
∫
0
x
f
(
x
)
d
x
⩾
(
n
+
1
)
∫
0
T
f
(
x
)
d
x
n\int^T_0f(x)\text{d}x\geqslant\int^x_0f(x)\text{d}x\geqslant(n+1)\int^{T}_0f(x)\text{d}x
n∫0Tf(x)dx⩾∫0xf(x)dx⩾(n+1)∫0Tf(x)dx
3. 既是奇函数又是周期函数的函数,每个周期内积分必为0.
(7) 变积分限函数前面有分式
在对带变积分限函数的方程两边求导时,必须保证变积分限函数前面没有下面这种带
x
\,x\,
x分式:
f
(
x
)
−
1
x
+
1
∫
0
x
t
f
(
t
)
d
t
=
1
f(x)-\frac{1}{x+1}\int^x_0tf(t)\text{d}t=1
f(x)−x+11∫0xtf(t)dt=1
必须先两边乘以 x + 1 \,x+1 x+1,否则变积分限函数永远清理不掉.
7 反常积分 (广义积分)
概念:
不满足可积条件的积分.
满足下列条件之一, f ( x ) f(x)\, f(x)在 [ a , b ] \,[a,b]\, [a,b]上可积:
1. f ( x ) ∈ C [ a , b ] f(x)\in C[a,b] f(x)∈C[a,b].
2. f ( x ) f(x)\, f(x)有界且在 [ a , b ] \,[a,b]\, [a,b]上存在有限个间断点 (即不含无穷间断点,可能含有第一类间断点或振荡间断点).
3. f ( x ) f(x)\, f(x)在 [ a , b ] \,[a,b]\, [a,b]上单调.
注意:由可积条件可知,并非有间断点就是反常积分!
所有情况一览:
{ 区 间 无 限 { ( a , + ∞ ) ( − ∞ , a ) ( − ∞ , + ∞ ) 区 间 有 限 ( 无 界 函 数 ) { ( a , b ] [ a , b ) [ a , c ) ∪ ( c , b ] \begin{cases}区间无限\begin{cases}(a,+\infty)\\(-\infty,a)\\(-\infty,+\infty)\end{cases}\\ 区间有限(无界函数)\begin{cases}(a,b]\\{[a,b)}\\{[a,c)\cup(c,b]}\end{cases}\end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧区间无限⎩⎪⎨⎪⎧(a,+∞)(−∞,a)(−∞,+∞)区间有限(无界函数)⎩⎪⎨⎪⎧(a,b][a,b)[a,c)∪(c,b]
(一) Γ \Gamma\, Γ函数
Γ ( α ) = ∫ 0 + ∞ x α − 1 e − x d x \Gamma(\alpha)=\int^{+\infty}_0x^{\alpha-1}e^{-x}\text{d}x Γ(α)=∫0+∞xα−1e−xdx
三个重要性质:
Γ ( α + 1 ) = α ⋅ Γ ( α ) \Gamma(\alpha+1)=\alpha\cdot\Gamma{(\alpha)} Γ(α+1)=α⋅Γ(α) Γ ( n + 1 ) = n ! \Gamma(n+1)=n! Γ(n+1)=n! Γ ( 1 2 ) = π \Gamma(\frac{1}{2})=\sqrt{\pi} Γ(21)=π
举例:
∫ 0 + ∞ x 5 e − x d x = Γ ( 6 ) = 5 ! \int^{+\infty}_0x^{{\color{Red}5}}e^{-x}\text{d}x=\Gamma({\color{Blue}6})={\color{Red}5}! ∫0+∞x5e−xdx=Γ(6)=5! ∫ 0 + ∞ x e − x d x = Γ ( 3 2 ) = 1 2 Γ ( 1 2 ) = π 2 \int^{+\infty}_0\sqrt{x}e^{-x}\text{d}x=\Gamma(\frac{3}{2})=\frac{1}{2}\,\Gamma(\frac{1}{2})=\frac{\sqrt{\pi}}{2} ∫0+∞xe−xdx=Γ(23)=21Γ(21)=2π ∫ 0 + ∞ x 3 2 e − x d x = Γ ( 5 2 ) = Γ ( 1 + 3 2 ) = 3 2 Γ ( 1 + 1 2 ) = 3 2 ⋅ 1 2 Γ ( 1 2 ) = 3 4 π \int^{+\infty}_0x^{\frac{3}{2}}e^{-x}\text{d}x=\Gamma(\frac{5}{2})=\Gamma(1+\frac{3}{2})=\frac{3}{2}\Gamma(1+\frac{1}{2})=\frac{3}{2}\cdot\frac{1}{2}\Gamma(\frac{1}{2})=\frac{3}{4}\pi ∫0+∞x23e−xdx=Γ(25)=Γ(1+23)=23Γ(1+21)=23⋅21Γ(21)=43π
(二) 无穷限积分 (积分区间无限)
设 ∫ a b f ( x ) d x = F ( b ) − F ( a ) \,\int_a^bf(x)\text{d}x=F(b)-F(a) ∫abf(x)dx=F(b)−F(a):
1 f ( x ) f(x)\, f(x)在 [ a , + ∞ ) \,[a,+\infty)\, [a,+∞)上连续
(1) 定义
收敛:若
lim
b
→
+
∞
[
F
(
b
)
−
F
(
a
)
]
=
A
\,\lim\limits_{b\to+\infty}[F(b)-F(a)]=A
b→+∞lim[F(b)−F(a)]=A,则反常积分
∫
a
+
∞
f
(
x
)
d
x
=
A
\int_a^{+\infty}f(x)\text{d}x=A
∫a+∞f(x)dx=A,收敛.
发散:若
lim
b
→
+
∞
[
F
(
b
)
−
F
(
a
)
]
\,\lim\limits_{b\to+\infty}[F(b)-F(a)]\,
b→+∞lim[F(b)−F(a)]不存在,则反常积分
∫
a
+
∞
f
(
x
)
d
x
\int_a^{+\infty}f(x)\text{d}x\,
∫a+∞f(x)dx发散.
(2) 判别法
lim
x
→
+
∞
x
α
f
(
x
)
=
C
0
(
≠
0
)
{
α
>
1
,
收
敛
α
⩽
1
,
发
散
\lim\limits_{x\to+\infty}x^\alpha f(x)=C_0\;(\neq 0)\begin{cases}\alpha>1,收敛 \\\alpha\leqslant1,发散\end{cases}
x→+∞limxαf(x)=C0(=0){α>1,收敛α⩽1,发散
2 f ( x ) f(x)\, f(x)在 ( − ∞ , a ] \,(-\infty,a]\, (−∞,a]上连续
(1) 定义
收敛:若
lim
b
→
−
∞
[
F
(
b
)
−
F
(
a
)
]
=
A
\,\lim\limits_{b\to-\infty}[F(b)-F(a)]=A
b→−∞lim[F(b)−F(a)]=A,则反常积分
∫
−
∞
a
f
(
x
)
d
x
=
A
\int^a_{-\infty}f(x)\text{d}x=A
∫−∞af(x)dx=A,收敛.
发散:若
lim
b
→
−
∞
[
F
(
b
)
−
F
(
a
)
]
\,\lim\limits_{b\to-\infty}[F(b)-F(a)]\,
b→−∞lim[F(b)−F(a)]不存在,则反常积分
∫
−
∞
a
f
(
x
)
d
x
\int^a_{-\infty}f(x)\text{d}x\,
∫−∞af(x)dx发散.
(2) 判别法
lim
x
→
−
∞
x
α
f
(
x
)
=
C
0
(
≠
0
)
{
α
>
1
,
收
敛
α
⩽
1
,
发
散
\lim\limits_{x\to-\infty}x^\alpha f(x)=C_0\;(\neq 0)\begin{cases}\alpha>1,收敛 \\\alpha\leqslant1,发散\end{cases}
x→−∞limxαf(x)=C0(=0){α>1,收敛α⩽1,发散
3 f ( x ) f(x)\, f(x)在 ( − ∞ , + ∞ ) \,(-\infty,+\infty)\, (−∞,+∞)上连续
若 ∫ − ∞ a f ( x ) d x \,\int^a_{-\infty}f(x)\text{d}x ∫−∞af(x)dx、 ∫ a + ∞ f ( x ) d x \int_a^{+\infty}f(x)\text{d}x\, ∫a+∞f(x)dx都收敛,则反常积分 ∫ − ∞ + ∞ f ( x ) d x \,\int^{+\infty}_{-\infty}f(x)\text{d}x\, ∫−∞+∞f(x)dx收敛,否则发散.
若 ∫ − ∞ + ∞ f ( x ) d x \,\int^{+\infty}_{-\infty}f(x)\text{d}x\, ∫−∞+∞f(x)dx收敛,则存在常数 A \,A A、 B B B,使得 ∫ − ∞ + ∞ f ( x ) d x = lim A → + ∞ B → − ∞ ∫ B A f ( x ) d x ∃ \,\int^{+\infty}_{-\infty}f(x)\text{d}x=\lim\limits_{A\to+\infty\atop B\to -\infty}\int^A_Bf(x)\text{d}x\exist ∫−∞+∞f(x)dx=B→−∞A→+∞lim∫BAf(x)dx∃.
(三) 瑕积分 (积分区间有限)
1 f ( x ) f(x)\, f(x)在 ( a , b ] \,(a,b]\, (a,b]上连续,在 x = a \,x=a\, x=a的右邻域内无界
设 ϵ > 0 \,\epsilon>0 ϵ>0, ∫ a + ϵ b f ( x ) d x = F ( b ) − F ( a + ϵ ) \,\int_{a+\epsilon}^{b}f(x)\text{d}x=F(b)-F(a+\epsilon) ∫a+ϵbf(x)dx=F(b)−F(a+ϵ):
(1) 定义
收敛:若
lim
ϵ
→
0
+
[
F
(
b
)
−
F
(
a
+
ϵ
)
]
=
A
\,\lim\limits_{\epsilon\to 0^+}[F(b)-F(a+\epsilon)]=A
ϵ→0+lim[F(b)−F(a+ϵ)]=A,则反常积分
∫
b
a
f
(
x
)
d
x
=
A
\int^a_{b}f(x)\text{d}x=A
∫baf(x)dx=A,收敛.
发散:若
lim
ϵ
→
0
+
[
F
(
b
)
−
F
(
a
+
ϵ
)
]
\,\lim\limits_{\epsilon\to 0^+}[F(b)-F(a+\epsilon)]\,
ϵ→0+lim[F(b)−F(a+ϵ)]不存在,则反常积分
∫
b
a
f
(
x
)
d
x
\int^a_{b}f(x)\text{d}x\,
∫baf(x)dx发散.
(2) 判别法
lim
x
→
a
+
(
x
−
a
)
α
f
(
x
)
=
C
0
(
≠
0
)
{
α
<
1
,
收
敛
α
⩾
1
,
发
散
\lim\limits_{x\to a^+}(x-a)^\alpha f(x)=C_0\;(\neq 0)\begin{cases}\alpha<1,收敛 \\\alpha\geqslant1,发散\end{cases}
x→a+lim(x−a)αf(x)=C0(=0){α<1,收敛α⩾1,发散
区间不能取到的端点(该点函数极限无穷)称为瑕点,带瑕点的反常积分称为瑕积分.
2 f ( x ) f(x)\, f(x)在 [ a , b ) \,[a,b)\, [a,b)上连续,在 x = b \,x=b\, x=b的左邻域内无界
设 ϵ > 0 \,\epsilon>0 ϵ>0, ∫ a b − ϵ f ( x ) d x = F ( b − ϵ ) − F ( a ) \,\int_{a}^{b-\epsilon}f(x)\text{d}x=F(b-\epsilon)-F(a) ∫ab−ϵf(x)dx=F(b−ϵ)−F(a):
(1) 定义
收敛:若
lim
ϵ
→
0
+
[
F
(
b
−
ϵ
)
−
F
(
a
)
]
=
A
\,\lim\limits_{\epsilon\to 0^+}[F(b-\epsilon)-F(a)]=A
ϵ→0+lim[F(b−ϵ)−F(a)]=A,则反常积分
∫
b
a
f
(
x
)
d
x
=
A
\int^a_{b}f(x)\text{d}x=A
∫baf(x)dx=A,收敛.
发散:若
lim
ϵ
→
0
+
[
F
(
b
−
ϵ
)
−
F
(
a
)
]
\,\lim\limits_{\epsilon\to 0^+}[F(b-\epsilon)-F(a)]\,
ϵ→0+lim[F(b−ϵ)−F(a)]不存在,则反常积分
∫
b
a
f
(
x
)
d
x
\int^a_{b}f(x)\text{d}x\,
∫baf(x)dx发散.
(2) 判别法
lim
x
→
b
−
(
b
−
x
)
α
f
(
x
)
=
C
0
(
≠
0
)
{
α
<
1
,
收
敛
α
⩾
1
,
发
散
\lim\limits_{x\to b^-}(b-x)^\alpha f(x)=C_0\;(\neq 0)\begin{cases}\alpha<1,收敛 \\\alpha\geqslant1,发散\end{cases}
x→b−lim(b−x)αf(x)=C0(=0){α<1,收敛α⩾1,发散
3 f ( x ) f(x)\, f(x)在 [ a , c ) ∪ ( c , b ] \,[a,c)\cup(c,b]\, [a,c)∪(c,b]上连续,在 x = c \,x=c\, x=c的去心领域内无界
若
∫
a
c
f
(
x
)
d
x
\,\int_{a}^{c}f(x)\text{d}x
∫acf(x)dx、
∫
c
b
f
(
x
)
d
x
\int_{c}^{b}f(x)\text{d}x\,
∫cbf(x)dx都收敛时,则反常积分
∫
b
a
f
(
x
)
d
x
\,\int^{a}_{b}f(x)\text{d}x\,
∫baf(x)dx收敛,且
∫
b
a
f
(
x
)
d
x
=
∫
a
c
f
(
x
)
d
x
+
∫
c
b
f
(
x
)
d
x
\int^{a}_{b}f(x)\text{d}x=\int_{a}^{c}f(x)\text{d}x+\int_{c}^{b}f(x)\text{d}x
∫baf(x)dx=∫acf(x)dx+∫cbf(x)dx
否则发散.
(四) 反常积分敛散性判别技巧
预备知识
无穷小与无穷大的关系:
(1) 无穷小的倒数是无穷大(趋近于
0
\,0\,
0的过程不等于
0
\,0\,
0),无穷大的倒数是无穷小;
(2) A A\, A和 B \,B\, B都是无穷大,且 A \,A\, A趋于无穷大的速度比 B \,B\, B快,那么 1 A \,\frac{1}{A}\, A1趋近于 0 \,0\, 0的速度就比 1 B \,\frac{1}{B}\, B1快;
A A\, A是比 B \,B\, B更高阶的无穷大 ⇒ \,\Rightarrow\, ⇒ 1 A \frac{1}{A}\, A1是比 1 B \,\frac{1}{B}\, B1更高阶的无穷大.
(3) A A\, A和 B \,B\, B都是无穷小,且 A \,A\, A趋于无穷小的速度比 B \,B\, B快,趋近于 0 \,0\, 0的过程 A B ≠ 0 \,AB\neq 0 AB=0,那么 1 A \,\frac{1}{A}\, A1趋近于无穷大的速度就比 1 B \,\frac{1}{B}\, B1快.
A A\, A是比 B \,B\, B更高阶的无穷小 ⇒ \,\Rightarrow\, ⇒ 1 A \frac{1}{A}\, A1是比 1 B \,\frac{1}{B}\, B1更高阶的无穷小.
ln
x
\text{ln}x\,
lnx任意次幂比牛还慢的两个重要结论:
x
→
0
+
x\to 0^+
x→0+时,
ln
x
\text{ln}x\,
lnx趋近于无穷的速度比
1
x
\,\frac{1}{x}\,
x1的任意次幂都要慢;
x
→
+
∞
x\to +\infty\,
x→+∞时,
ln
x
\text{ln}x\,
lnx趋近于无穷的速度比
x
\,x\,
x的任意次幂都要慢;
(1) 三种基本反常积分 (可以直接积出来)
以下三种反常积分通过直接积出来的办法可以直接检验是否收敛,使用频繁,需要记忆.
(1) 无穷限积分
∫
a
+
∞
d
x
x
p
=
{
发
散
,
0
<
p
⩽
1
,
收
敛
,
p
>
1.
(
a
>
0
,
p
>
0
)
\int^{+\infty}_a\frac{\text{d}x}{x^p}= \begin{cases}发散,&0<p\leqslant 1,\\ 收敛,&p>1. \end{cases}\;\;(a>0,\,p>0)
∫a+∞xpdx={发散,收敛,0<p⩽1,p>1.(a>0,p>0)
理解:积分区间延展到无穷,要想收敛,被积函数就要尽可能小,即 p \,p\, p要尽可能大. 记住这个界限是 1 \,1\, 1.
(2) 瑕积分
∫
a
b
d
x
(
x
−
a
)
q
=
{
发
散
,
q
⩾
1
,
收
敛
,
0
<
q
<
1.
(
q
>
0
)
\int^{b}_a\frac{\text{d}x}{(x-a)^q}= \begin{cases}发散,&q\geqslant1,\\ 收敛,&0<q<1. \end{cases}\;\;(q>0)
∫ab(x−a)qdx={发散,收敛,q⩾1,0<q<1.(q>0)
理解:瑕积分是某点 ( x = a x=a x=a) 的函数值趋近于无穷,要想收敛,同样要使被积函数尽可能小,当 x → a \,x\to a\, x→a时, ( x − a ) (x-a)\, (x−a)是一个很小的数,所以 q \,q\, q也要尽可能小. 记住这个界限是 1 \,1\, 1.
为帮助记忆以上结论,可以通俗理解为:“大的喜欢大的,小的喜欢小的”,并且 p \,p\, p或 q \,q\, q等于 1 \,1 1,积分发散.
“大的喜欢大的,小的喜欢小的”:上面的无穷限积分区间很大,就要 p \,p\, p足够大,而上面的瑕积分区间小,就要 q \,q\, q足够小.
(3) 无穷限积分 (带
ln
\,\ln
ln)
∫
a
+
∞
d
x
x
p
ln
q
x
=
{
收
敛
,
p
>
1
,
收
敛
,
p
=
1
且
q
>
1
,
发
散
,
p
=
1
且
q
⩽
1
,
发
散
,
p
<
1.
(
a
>
1
)
\int^{+\infty}_a\frac{\text{d}x}{x^p\text{ln}^qx}= \begin{cases}收敛,&p>1,\\ 收敛,&p=1\,且\,q>1,\\ 发散,&p=1\,且\,q\leqslant1,\\ 发散,&p<1.\\ \end{cases}\;\;(a>1)
∫a+∞xplnqxdx=⎩⎪⎪⎪⎨⎪⎪⎪⎧收敛,收敛,发散,发散,p>1,p=1且q>1,p=1且q⩽1,p<1.(a>1)
理解:类比第 ( 1 ) \,(1)\, (1)种反常积分,也是需要让分母足够小,即 p \,p\, p和 q \,q\, q足够大. 现在是 p \,p\, p和 q \,q\, q共同控制积分的敛散性. 指数函数比对数函数决定权更大. 当 p > 1 \,p>1\, p>1时,无论如何积分都收敛. 当 p = 1 \,p=1\, p=1时情况比较特殊,需要额外考虑 q \,q\, q的大小来决定敛散性,当 p < 1 \,p<1\, p<1时,无论如何积分都发散.
(2) 找等价或同阶无穷小
定理1 (用于判别无穷限积分):
设函数
f
(
x
)
\,f(x)\,
f(x)在区间
[
a
,
+
∞
)
\,[a,\,+\infty)\,
[a,+∞)上连续,且
f
(
x
)
⩾
0
\,f(x)\geqslant0
f(x)⩾0. 若存在常数
p
>
1
\,p>1
p>1,使得
lim
x
→
+
∞
x
p
f
(
x
)
\,\lim\limits_{x\to+\infty}x^p f(x)\,
x→+∞limxpf(x)存在,那么反常积分
∫
a
+
∞
f
(
x
)
d
x
\,\int^{+\infty}_af(x)\text{d}x\,
∫a+∞f(x)dx收敛;如果
lim
x
→
+
∞
x
f
(
x
)
=
d
>
0
\,\lim\limits_{x\to+\infty}x f(x)=d>0\,
x→+∞limxf(x)=d>0(或
d
=
+
∞
\,d=+\infty
d=+∞),反常积分发散.
定理1使用:
(1) 相当于找
x
→
∞
\,x\to\infty\,
x→∞时,被积函数
f
(
x
)
\,f(x)\,
f(x)的等价或同阶无穷小
1
x
p
\,\frac{1}{x^p}
xp1,
∫
a
+
∞
f
(
x
)
d
x
\int_a^{+\infty}f(x)\text{d}x
∫a+∞f(x)dx与
∫
a
+
∞
1
x
p
d
x
\int_a^{+\infty}\frac{1}{x^p}\text{d}x\,
∫a+∞xp1dx同敛散,而后者是三种常见反常积分的第一种,很好判断.
(2) 若找不到同阶无穷小,还可用比较的方法. 假设能找到比
f
(
x
)
\,f(x)\,
f(x)更高阶无穷小
1
x
p
\,\frac{1}{x^p}
xp1(趋近于
0
\,0\,
0的速度比
f
(
x
)
\,f(x)\,
f(x)快),若
∫
a
+
∞
1
x
p
d
x
\,\int_a^{+\infty}\frac{1}{x^p}\text{d}x\,
∫a+∞xp1dx发散,那么
∫
a
+
∞
f
(
x
)
d
x
\,\int_a^{+\infty}f(x)\text{d}x\,
∫a+∞f(x)dx也发散. 同样,若能找到比
f
(
x
)
\,f(x)\,
f(x)更低阶无穷小
1
x
p
\,\frac{1}{x^p}
xp1(趋近于
0
\,0\,
0的速度比
f
(
x
)
\,f(x)\,
f(x)慢),若
∫
a
+
∞
1
x
p
d
x
\,\int_a^{+\infty}\frac{1}{x^p}\text{d}x\,
∫a+∞xp1dx收敛,那么
∫
a
+
∞
f
(
x
)
d
x
\,\int_a^{+\infty}f(x)\text{d}x\,
∫a+∞f(x)dx也收敛.
定理2 (用于判别瑕积分):
设函数
f
(
x
)
\,f(x)\,
f(x)在区间
(
a
,
b
]
\,(a,\,b]\,
(a,b]上连续,且
f
(
x
)
⩾
0
\,f(x)\geqslant0
f(x)⩾0.
x
=
a
x=a\,
x=a为
f
(
x
)
\,f(x)\,
f(x)的瑕点. 若存在常数
0
<
q
<
1
\,0<q<1
0<q<1,使得
lim
x
→
+
∞
(
x
−
a
)
q
f
(
x
)
\,\lim\limits_{x\to+\infty}(x-a)^q f(x)\,
x→+∞lim(x−a)qf(x)存在,那么反常积分
∫
a
b
f
(
x
)
d
x
\,\int^{b}_af(x)\text{d}x\,
∫abf(x)dx收敛;如果
lim
x
→
a
+
(
x
−
a
)
f
(
x
)
=
d
>
0
\,\lim\limits_{x\to a^+}(x-a) f(x)=d>0\,
x→a+lim(x−a)f(x)=d>0(或
d
=
+
∞
\,d=+\infty
d=+∞),反常积分发散.
定理2使用:
(1) 找到在瑕点附近,被积函数
f
(
x
)
\,f(x)\,
f(x)的等价或同阶无穷大. (无穷大的倒数是无穷小,所以相当于找分母的等价或同阶无穷小),二者瑕积分同敛散.
(2) 找不到同阶无穷大,也可用比较的方法.
(3) 两个瑕点、上下限都是无穷、既有瑕点又是无穷限积分
思路:选取某些点将反常积分进行拆分,使得每一个积分都可以被单独研究. 该点的选取是随意的.
例. 设 m \,m m、 n n\, n是正整数,判断 m \,m m、 n n\, n与下面反常积分敛散性的关系:
∫ 0 1 ln 2 ( 1 − x ) m x n d x \int^1_0\frac{\sqrt[m]{\text{ln}^2(1-x)}}{\sqrt[n]x}\text{d}x ∫01nxmln2(1−x)dx解:该积分有两个瑕点 ( x = 0 x=0\, x=0和 x = 1 \,x=1 x=1),故先做如下拆分,分开考虑:
∫ 0 1 ln 2 ( 1 − x ) m x n d x = ∫ 0 1 2 ln 2 ( 1 − x ) m x n d x + ∫ 1 2 1 ln 2 ( 1 − x ) m x n d x \int^1_0\frac{\sqrt[m]{\text{ln}^2(1-x)}}{\sqrt[n]x}\text{d}x=\int^\frac{1}{2}_0\frac{\sqrt[m]{\text{ln}^2(1-x)}}{\sqrt[n]x}\text{d}x+\int^1_\frac{1}{2}\frac{\sqrt[m]{\text{ln}^2(1-x)}}{\sqrt[n]x}\text{d}x ∫01nxmln2(1−x)dx=∫021nxmln2(1−x)dx+∫211nxmln2(1−x)dx(1) 对于 ∫ 0 1 2 ln 2 ( 1 − x ) m x n d x \,\int^\frac{1}{2}_0\frac{\sqrt[m]{\text{ln}^2(1-x)}}{\sqrt[n]x}\text{d}x ∫021nxmln2(1−x)dx,应当使用定理2进行判断,尝试找被积函数在 x → 0 \,x\to 0\, x→0时的等价或同阶无穷大. 先找倒数的无穷小:
x n ln 2 ( 1 − x ) m ∼ x 1 n [ ln ( 1 − x ) ] 2 m ∼ x 1 n x 2 m = x 1 n − 2 m \frac{\sqrt[n]x}{\sqrt[m]{\text{ln}^2(1-x)}}\sim\frac{x^{\frac{1}{n}}}{[\text{ln}(1-x)]^{\frac{2}{m}}}\sim \frac{x^{\frac{1}{n}}}{x^{\frac{2}{m}}}=x^{\frac{1}{n}-\frac{2}{m}} mln2(1−x)nx∼[ln(1−x)]m2xn1∼xm2xn1=xn1−m2所以 ln 2 ( 1 − x ) m x n \frac{\sqrt[m]{\text{ln}^2(1-x)}}{\sqrt[n]x}\, nxmln2(1−x)对应的等价无穷大就是: 1 x 1 n − 2 m \frac{1}{x^{\frac{1}{n}-\frac{2}{m}}} xn1−m21
因为 m \,m m、 n n\, n是正整数,所以 1 n − 2 m < 1 n ⩽ 1 \,{\frac{1}{n}-\frac{2}{m}}<\frac{1}{n}\leqslant 1 n1−m2<n1⩽1, ∫ 0 1 2 1 x 1 n − 2 m d x \int^\frac{1}{2}_0\frac{1}{x^{\frac{1}{n}-\frac{2}{m}}}\text{d}x\, ∫021xn1−m21dx收敛,
所以 ∫ 0 1 2 ln 2 ( 1 − x ) m x n d x \,\int^\frac{1}{2}_0\frac{\sqrt[m]{\text{ln}^2(1-x)}}{\sqrt[n]x}\text{d}x\, ∫021nxmln2(1−x)dx也收敛.(2) 对于 ∫ 1 2 1 ln 2 ( 1 − x ) m x n d x \,\int^1_\frac{1}{2}\frac{\sqrt[m]{\text{ln}^2(1-x)}}{\sqrt[n]x}\text{d}x ∫211nxmln2(1−x)dx,应当使用定理2进行判断,尝试找被积函数在 x → 1 − \,x\to1^-\, x→1−时的等价或同阶无穷大:
ln 2 ( 1 − x ) m x n ∼ [ ln ( 1 − x ) ] 2 m x 1 n ∼ [ ln ( 1 − x ) ] 2 m \frac{\sqrt[m]{\text{ln}^2(1-x)}}{\sqrt[n]x}\sim\frac{[\text{ln}(1-x)]^{\frac{2}{m}}}{x^{\frac{1}{n}}}\sim [\text{ln}(1-x)]^{\frac{2}{m}} nxmln2(1−x)∼xn1[ln(1−x)]m2∼[ln(1−x)]m2
因为当 x → 0 + \,x\to 0^+ x→0+时, ln x \text{ln}x\, lnx趋近于无穷的速度比 1 x \,\frac{1}{x}\, x1的任意次幂都要慢,
所以当 x → 1 − \,x\to 1^- x→1−时, ln ( 1 − x ) \text{ln}(1-x)\, ln(1−x)趋近于无穷的速度比 1 1 − x \,\frac{1}{1-x}\, 1−x1的任意次幂都要慢,
而 ∫ 1 2 1 1 1 − x d x \int^1_\frac{1}{2}\frac{1}{{\sqrt{1-x}}}\text{d}x\, ∫2111−x1dx收敛 (不选 1 1 − x \,\frac{1}{1-x}\, 1−x1是因为 ∫ 1 2 1 1 1 − x d x \int^1_\frac{1}{2}\frac{1}{{1-x}}\text{d}x\, ∫2111−x1dx发散),
所以 ∫ 1 2 1 ln 2 ( 1 − x ) m x n d x \,\int^1_\frac{1}{2}\frac{\sqrt[m]{\text{ln}^2(1-x)}}{\sqrt[n]x}\text{d}x ∫211nxmln2(1−x)dx也收敛.
综上:原反常积分的敛散性与 m \,m m、 n n\, n取值无关.
(五) 反常积分相关性质总结
(1) 对于无穷限积分 ∫ 0 + ∞ f ( x ) d x \,\int^{+\infty}_{0}f(x)\text{d}x\, ∫0+∞f(x)dx和 ∫ − ∞ 0 f ( x ) d x \,\int^{0}_{-\infty}f(x)\text{d}x ∫−∞0f(x)dx,只要其中之一发散,则 ∫ − ∞ + ∞ f ( x ) d x \,\int^{+\infty}_{-\infty}f(x)\text{d}x\, ∫−∞+∞f(x)dx发散.
换言之, ∫ − ∞ + ∞ f ( x ) d x \,\int^{+\infty}_{-\infty}f(x)\text{d}x\, ∫−∞+∞f(x)dx收敛,当且仅当 ∫ 0 + ∞ f ( x ) d x \,\int^{+\infty}_{0}f(x)\text{d}x\, ∫0+∞f(x)dx和 ∫ − ∞ 0 f ( x ) d x \,\int^{0}_{-\infty}f(x)\text{d}x\, ∫−∞0f(x)dx都收敛. 反常积分不收敛,不能使用奇偶性质.
(2) 若 ∫ − ∞ + ∞ f ( x ) d x \,\int^{+\infty}_{-\infty}f(x)\text{d}x\, ∫−∞+∞f(x)dx收敛,则 ∫ − ∞ + ∞ f ( x ) d x = { 0 , f ( x ) 是 奇 函 数 , 2 ∫ 0 + ∞ f ( x ) d x , f ( x ) 是 偶 函 数 . \int^{+\infty}_{-\infty}f(x)\text{d}x=\begin{cases}0,&f(x)是奇函数,\\2\int^{+\infty}_0f(x)\text{d}x,&f(x)是偶函数.\end{cases} ∫−∞+∞f(x)dx={0,2∫0+∞f(x)dx,f(x)是奇函数,f(x)是偶函数.
反常积分一定要小心发散的情况. 反常积分收敛,才能使用奇偶性质.
比如: ∫ − ∞ + ∞ sin x d x \int^{+\infty}_{-\infty}\text{sin}x\text{d}x ∫−∞+∞sinxdx:由 ∫ 0 + ∞ sin x d x \,\int^{+\infty}_{0}\text{sin}x\text{d}x\, ∫0+∞sinxdx发散,可知 ∫ − ∞ + ∞ sin x d x \,\int^{+\infty}_{-\infty}\text{sin}x\text{d}x\, ∫−∞+∞sinxdx发散,并不等于 0 \,0 0.
(3) 若 ∫ − ∞ + ∞ f ( x ) d x \,\int^{+\infty}_{-\infty}f(x)\text{d}x\, ∫−∞+∞f(x)dx收敛,则有 lim R → + ∞ ∫ − R R f ( x ) d x ∃ \lim\limits_{R\to+\infty}\int^R_{-R}f(x)\text{d}x\,\exist R→+∞lim∫−RRf(x)dx∃
反之,若 lim R → + ∞ ∫ − R R f ( x ) d x ∃ \,\lim\limits_{R\to+\infty}\int^R_{-R}f(x)\text{d}x\,\exist R→+∞lim∫−RRf(x)dx∃, ∫ − ∞ + ∞ f ( x ) d x \int^{+\infty}_{-\infty}f(x)\text{d}x\, ∫−∞+∞f(x)dx不一定收敛.
比如 lim R → + ∞ ∫ − R R sin x d x = 0 \,\lim\limits_{R\to+\infty}\int^R_{-R}\text{sin}x\text{d}x=0 R→+∞lim∫−RRsinxdx=0,但 ∫ − ∞ + ∞ sin x d x \,\int^{+\infty}_{-\infty}\text{sin}x\text{d}x\, ∫−∞+∞sinxdx不存在. (3)本质上同(1)、(2)一样,是因为反常积分定义要求两段必须都收敛,整段才收敛.
(4) 对于无穷限积分 ∫ a + ∞ f ( x ) d x \,\int^{+\infty}_{a}f(x)\text{d}x ∫a+∞f(x)dx、 ∫ a + ∞ g ( x ) d x \int^{+\infty}_{a}g(x)\text{d}x\, ∫a+∞g(x)dx,有以下结论:
∫ a + ∞ f ( x ) d x \int^{+\infty}_{a}f(x)\text{d}x\, ∫a+∞f(x)dx收敛, ∫ a + ∞ g ( x ) d x \int^{+\infty}_{a}g(x)\text{d}x\, ∫a+∞g(x)dx收敛,则 ∫ a + ∞ [ f ( x ) ± g ( x ) ] d x \,\int^{+\infty}_{a}[f(x)\pm g(x)]\text{d}x\, ∫a+∞[f(x)±g(x)]dx收敛.
∫
a
+
∞
f
(
x
)
d
x
\int^{+\infty}_{a}f(x)\text{d}x\,
∫a+∞f(x)dx收敛,
∫
a
+
∞
g
(
x
)
d
x
\int^{+\infty}_{a}g(x)\text{d}x\,
∫a+∞g(x)dx发散,则
∫
a
+
∞
[
f
(
x
)
±
g
(
x
)
]
d
x
\,\int^{+\infty}_{a}[f(x)\pm g(x)]\text{d}x\,
∫a+∞[f(x)±g(x)]dx发散.
p[[[[[[
∫
a
+
∞
f
(
x
)
d
x
\int^{+\infty}_{a}f(x)\text{d}x\,
∫a+∞f(x)dx发散,
∫
a
+
∞
g
(
x
)
d
x
\int^{+\infty}_{a}g(x)\text{d}x\,
∫a+∞g(x)dx发散,则
∫
a
+
∞
[
f
(
x
)
±
g
(
x
)
]
d
x
\,\int^{+\infty}_{a}[f(x)\pm g(x)]\text{d}x\,
∫a+∞[f(x)±g(x)]dx敛散性不确定.
8 定积分的几何应用
(一) 特殊曲线总结
务必要十分熟悉下面的曲线和相关方程:
(1) y y\, y轴圆
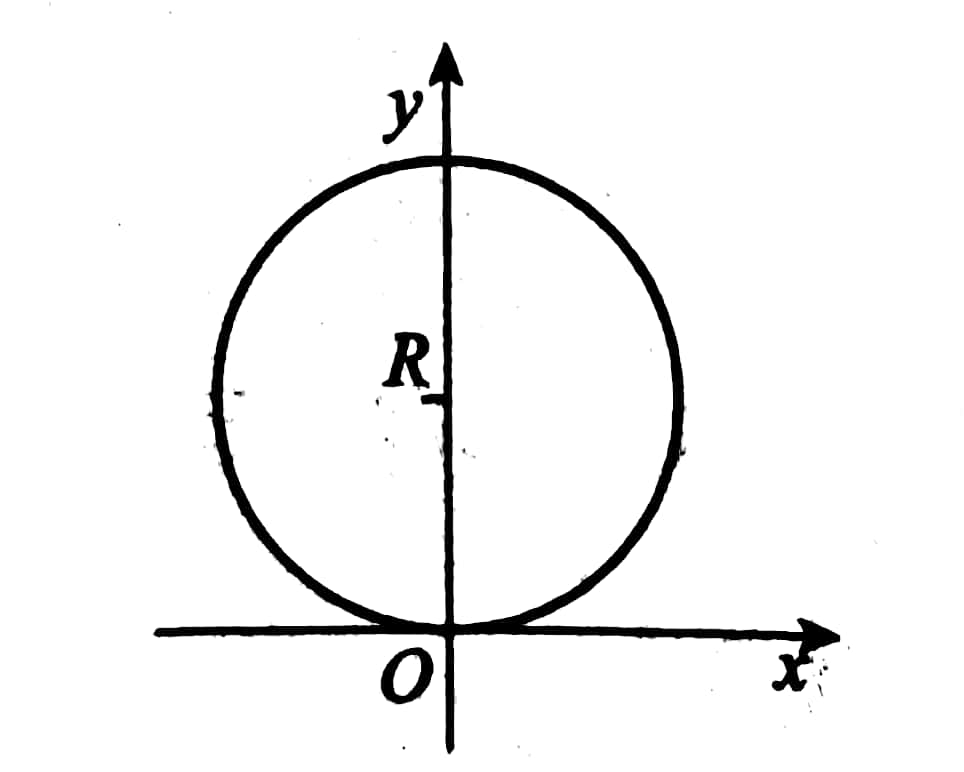
x 2 + y 2 = 2 R x \color{Blue}x^2+y^2=2Rx x2+y2=2Rx r = 2 R cos θ \color{Red}r=2R\,\text{cos}\theta r=2Rcosθ
(2) x x\, x轴圆
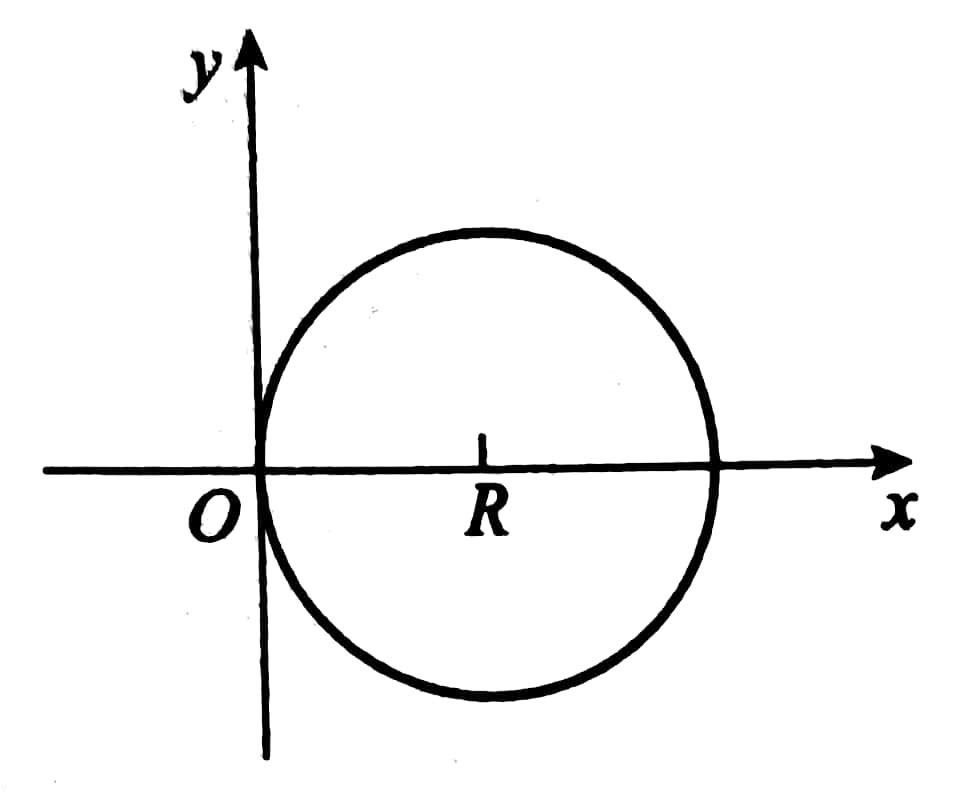
x 2 + y 2 = 2 R y \color{Blue}x^2+y^2=2Ry x2+y2=2Ry r = 2 R sin θ \color{Red}r=2R\,\text{sin}\theta r=2Rsinθ
(3) 摆线
生成:一个圆沿一条直线运动时,圆边界上一定点所形成的轨迹:
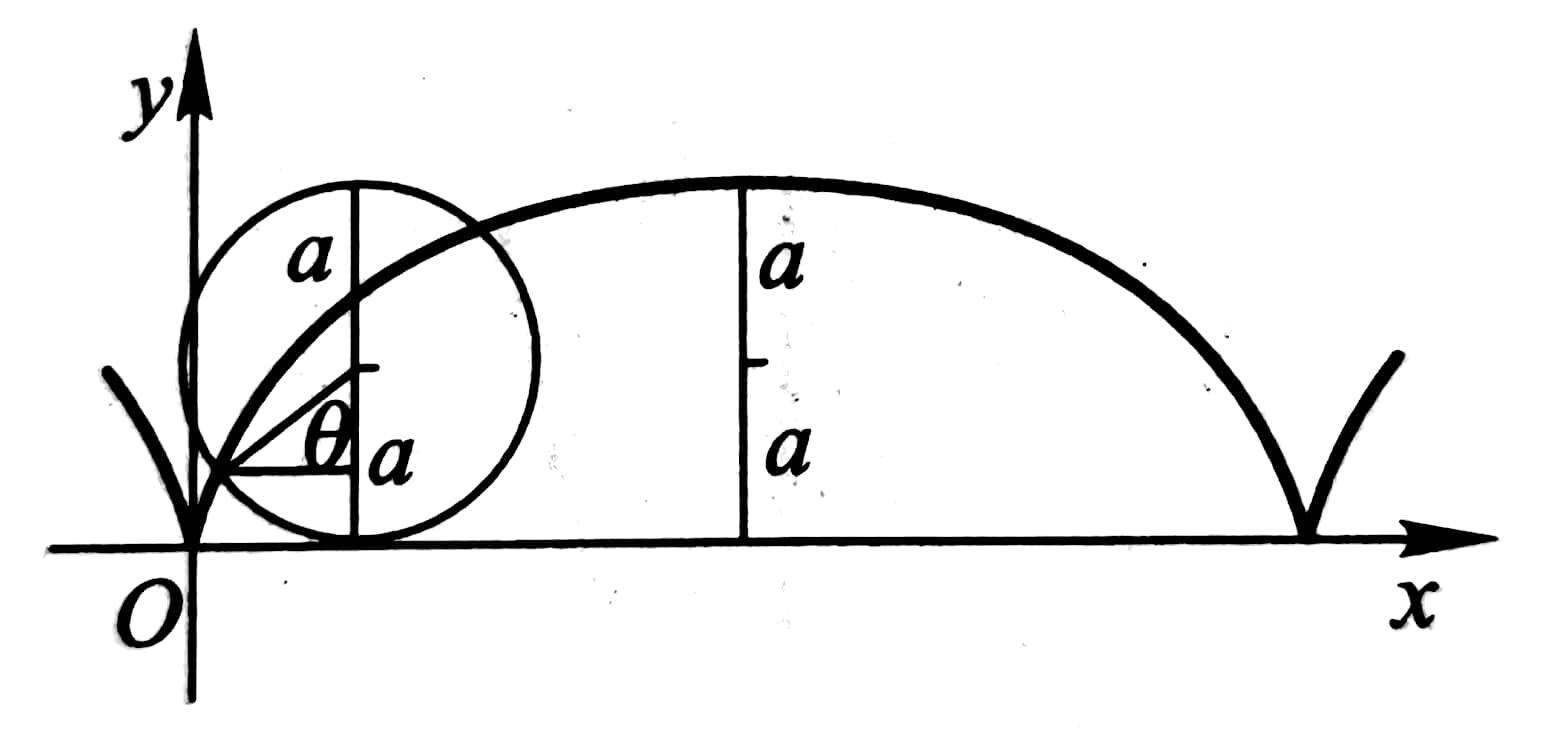
上图与 x \,x\, x轴交点分别为 x = 0 \,x=0\, x=0和 x = 2 π a \,x=2\pi a x=2πa.
摆线的参数方程:
{
x
=
a
(
θ
−
sin
θ
)
y
=
a
(
1
−
cos
θ
)
\begin{cases}\color{Purple}x=a(\theta-\text{sin}\theta)\\\color{Purple}y=a(1-\text{cos}\theta)\end{cases}
{x=a(θ−sinθ)y=a(1−cosθ)
注意:
(1)
x
\,x\,
x的方程中是
θ
−
sin
θ
\,{\color{Red}\theta}-\text{sin}\theta
θ−sinθ.
(2)
0
⩽
θ
⩽
2
π
0\leqslant\theta\leqslant2\pi\,
0⩽θ⩽2π或
0
⩽
x
⩽
2
π
a
\,0\leqslant x\leqslant2\pi a\,
0⩽x⩽2πa对应摆线的一拱.
(3) 心形线
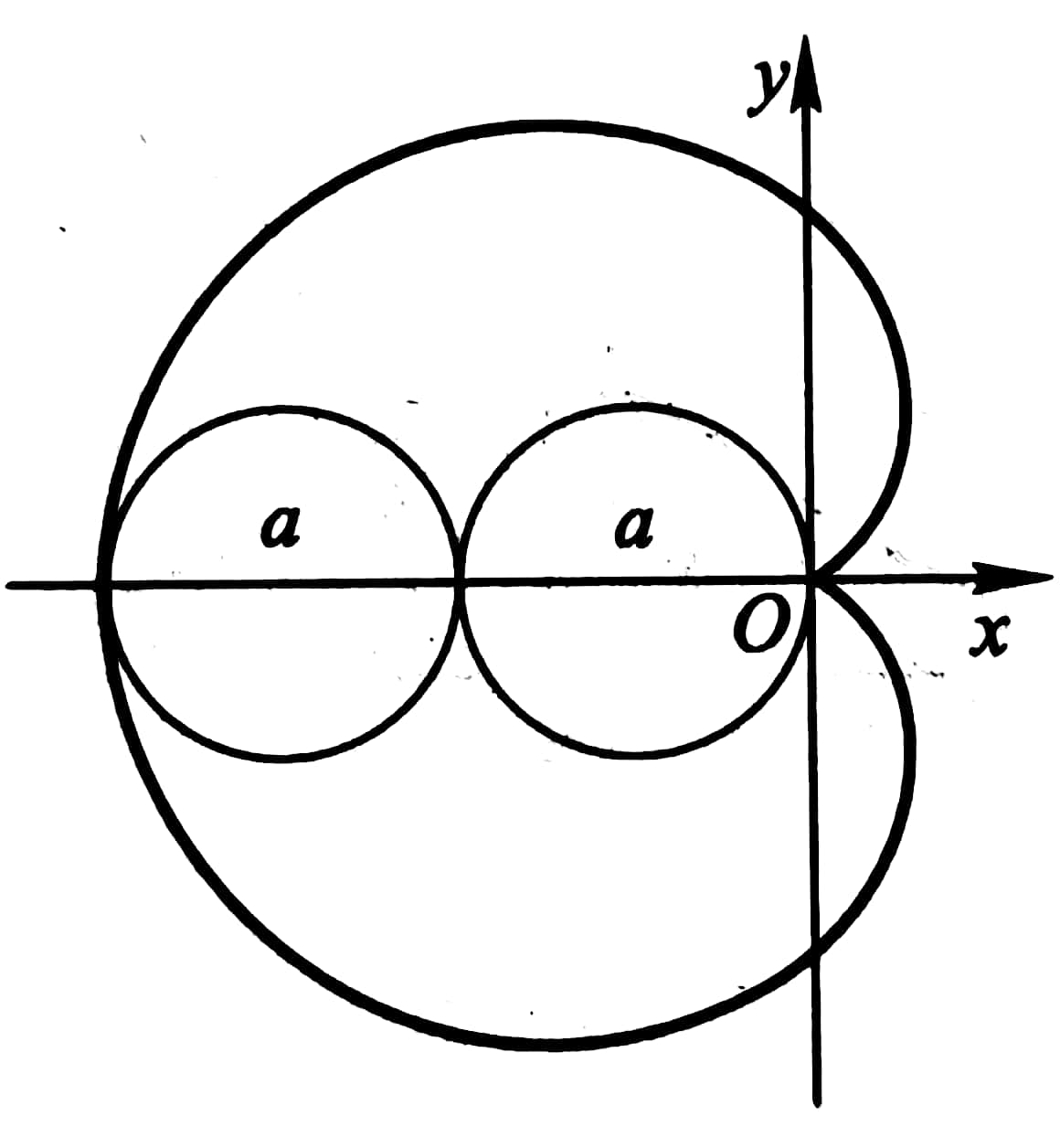
极坐标方程:
r
=
a
(
1
−
cos
θ
)
\color{Red}r=a(1-\text{cos}\theta)
r=a(1−cosθ)
如果心尖朝向相反方向 (即上图心形线的关于
y
\,y\,
y轴对称的图形),其极坐标方程为
r
=
a
(
1
+
cos
θ
)
\color{Red}r=a(1+\text{cos}\theta)
r=a(1+cosθ)
可以认为 cos θ \,\text{cos}\theta\, cosθ系数的正负决定了心尖朝向正半轴还是负半轴.
心形线所围面积: s = 3 2 π a 2 s=\frac{3}{2}\pi a^2 s=23πa2.
(4) 星型线
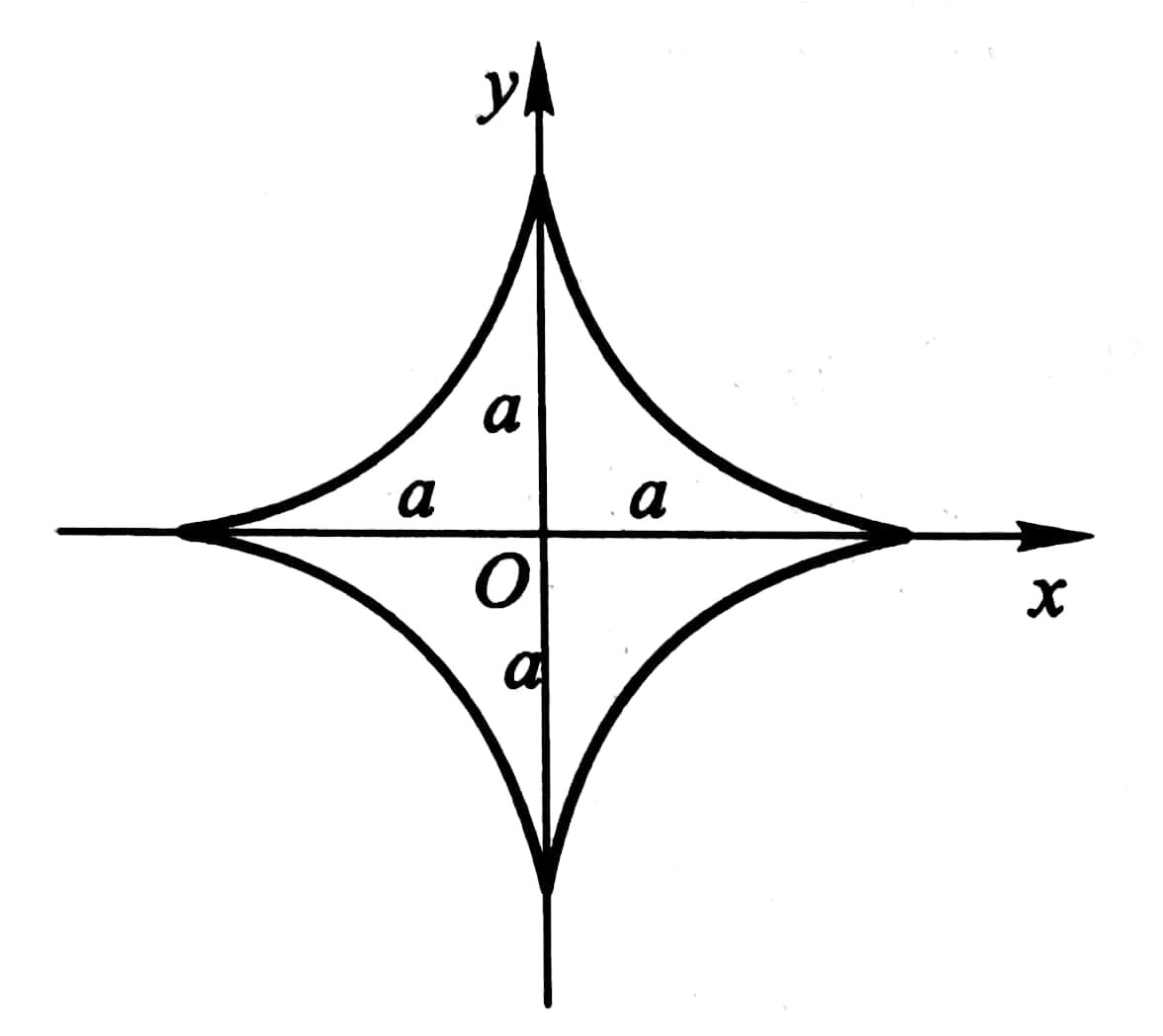
直角坐标方程:
x
2
3
+
y
2
3
=
a
2
3
\color{Blue}x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}
x32+y32=a32
参数方程:
{
x
=
a
cos
3
t
y
=
a
sin
3
t
\begin{cases}\color{Purple}x=a\,\text{cos}^3t\\\color{Purple}y=a\,\text{sin}^3t\end{cases}
{x=acos3ty=asin3t
(5) 双扭线
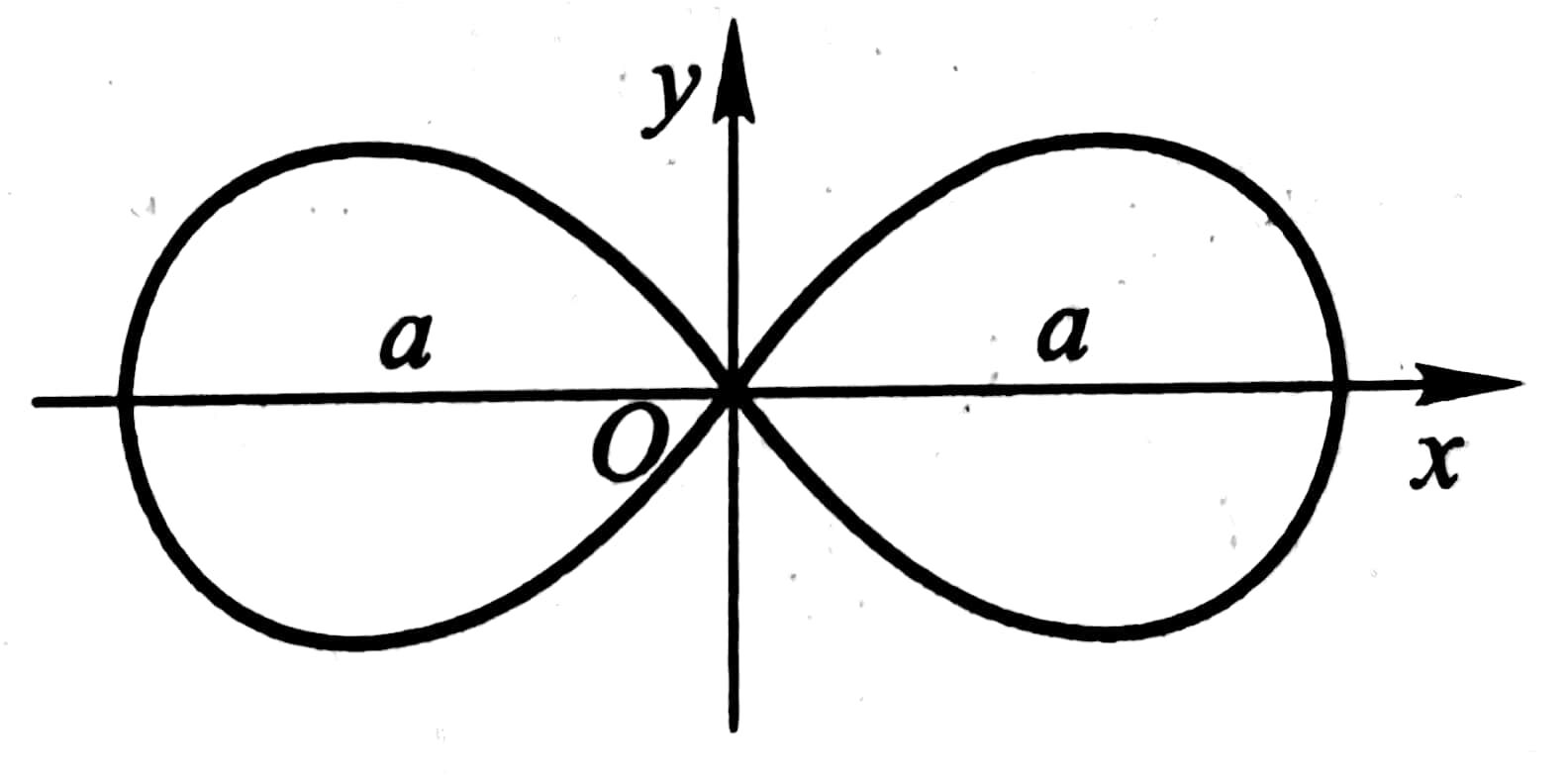
直角坐标方程:
(
x
2
+
y
2
)
2
=
a
2
(
x
2
−
y
2
)
\color{Blue}(x^2+y^2)^2=a^2(x^2-y^2)
(x2+y2)2=a2(x2−y2)
极坐标方程:
r
2
=
a
2
cos
2
θ
\color{Red}r^2=a^2\text{cos}2\theta
r2=a2cos2θ
注意:双纽线具有 y = ± x \,y=\pm x\, y=±x两条切线,因此每个象限角度范围为 0 ~ 45 ° \,0~45\degree 0~45°,第一象限 θ ∈ [ 0 , π 4 ] \,\theta\in[0,\frac{\pi}{4}] θ∈[0,4π].
sin \text{sin}\, sin型双扭线:
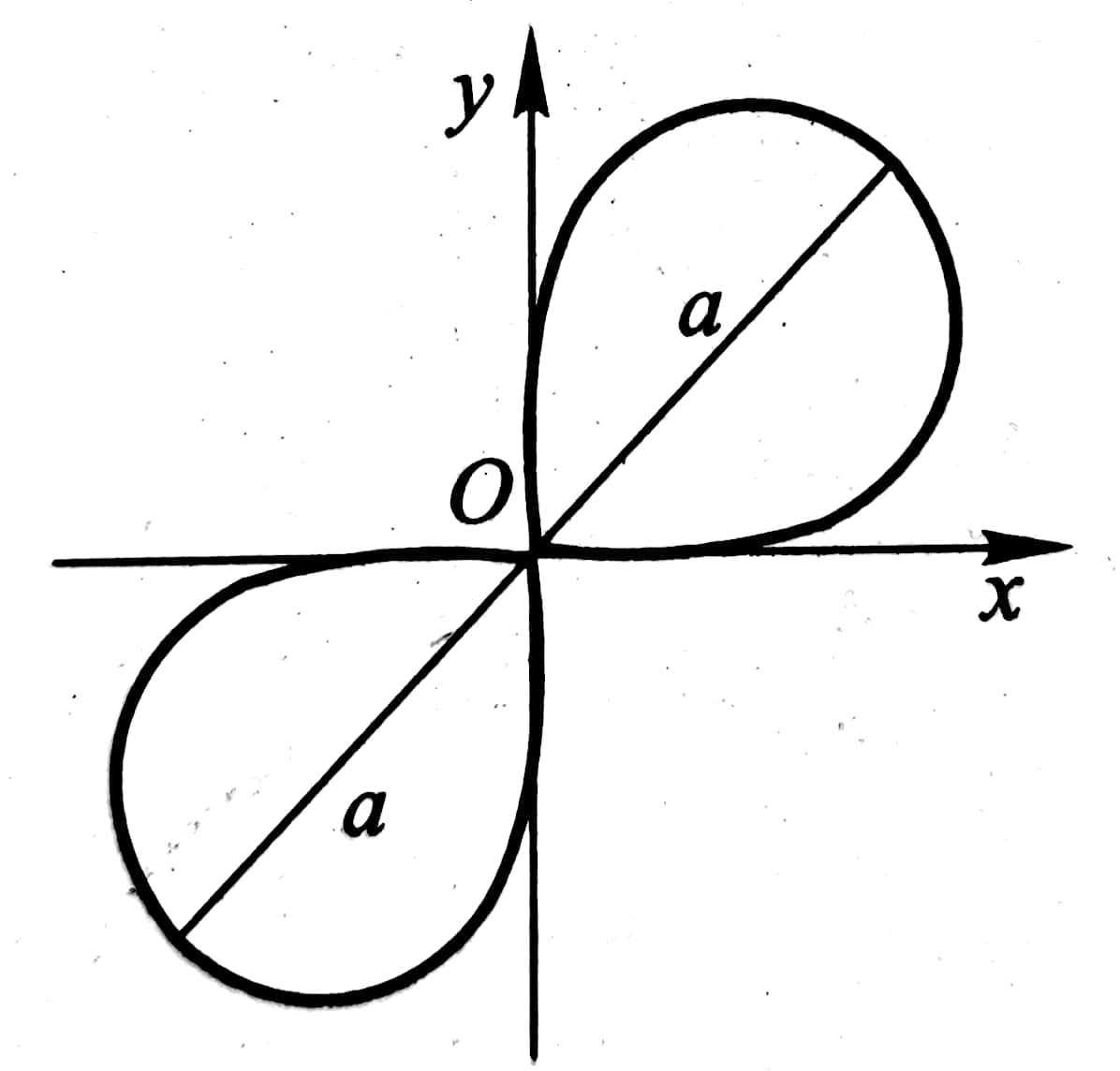
( x 2 + y 2 ) 2 = 2 a 2 x y \color{Blue}(x^2+y^2)^2=2a^2xy (x2+y2)2=2a2xy r 2 = a 2 sin 2 θ \color{Red}r^2=a^2\text{sin}2\theta r2=a2sin2θ
(二) 面积
1 直角坐标平面面积
(1) 由
y
=
f
(
x
)
⩾
0
\,y=f(x)\geqslant0
y=f(x)⩾0,
x
=
a
x=a\,
x=a及
x
=
b
(
a
<
b
)
\,x=b\;(a<b)\,
x=b(a<b)围成的面积:
A
=
∫
a
b
f
(
x
)
d
x
{\color{Blue}A=\int^b_af(x)\text{d}x}
A=∫abf(x)dx
(2) 由
y
=
f
(
x
)
\,y=f(x)
y=f(x),
y
=
g
(
x
)
y=g(x)
y=g(x),
x
=
a
x=a\,
x=a及
x
=
b
(
a
<
b
)
\,x=b\;(a<b)\,
x=b(a<b)围成的面积:
A
=
∫
a
b
∣
f
(
x
)
−
g
(
x
)
∣
d
x
{\color{Blue}A=\int^b_a\big|f(x)-g(x)\big|\text{d}x}
A=∫ab∣∣f(x)−g(x)∣∣dx
2 极坐标平面面积
(3) 由 r = r ( θ ) ( a ⩽ θ ⩽ b ) \,r=r(\theta)\;(a\leqslant\theta\leqslant b)\, r=r(θ)(a⩽θ⩽b)围成的面积:
A = 1 2 ∫ α β r 2 ( θ ) d θ {\color{Blue}A=\frac{1}{2}\int_{\alpha}^\beta r^2(\theta)\text{d}\theta} A=21∫αβr2(θ)dθ
(4) 由
r
=
r
1
(
θ
)
\,r=r_1(\theta)
r=r1(θ),
r
=
r
2
(
θ
)
(
r
1
(
θ
)
⩽
r
2
(
θ
)
,
a
⩽
θ
⩽
b
)
r=r_2(\theta)\;(r_1(\theta)\leqslant r_2(\theta),a\leqslant\theta\leqslant b)\,
r=r2(θ)(r1(θ)⩽r2(θ),a⩽θ⩽b)围成的面积:
A
=
1
2
∫
α
β
[
r
2
2
(
θ
)
−
r
1
2
(
θ
)
]
d
θ
{\color{Blue}A=\frac{1}{2}\int_{\alpha}^\beta [r_2^2(\theta)-r_1^2(\theta)]\text{d}\theta}
A=21∫αβ[r22(θ)−r12(θ)]dθ
3 旋转曲面侧面积
L : y = f ( x ) ( a ⩽ x ⩽ b ) L:y=f(x)\;(a\leqslant x\leqslant b)\, L:y=f(x)(a⩽x⩽b)绕 x \,x\, x轴旋转所得旋转体的侧面积:
1 o 1^o\;\; 1o取 [ x , x + d x ] ⊂ [ a , b ] [x,x+\text{d}x]\subset[a,b] [x,x+dx]⊂[a,b].
2 o 2^o\;\; 2o d A = 2 π ∣ f ( x ) ∣ d s \text{d}A=2\pi|f(x)|\text{d}s dA=2π∣f(x)∣ds
3 o 3^o\;\; 3o A = ∫ a b d A A=\int^b_a\text{d}A A=∫abdA
A = ∫ a b ∣ f ( x ) ∣ ⋅ 1 + f ′ 2 ( x ) d x {\color{Blue}A=\int^b_a\big|f(x)\big|\cdot\sqrt{1+f'^2(x)}\text{d}x} A=∫ab∣∣f(x)∣∣⋅1+f′2(x)dx
- 可以不需要记忆,但是要知道怎么求.
L : { x = φ ( t ) y = ψ ( t ) ( α ⩽ θ ⩽ β ) L:\begin{cases}x=\varphi(t)\\y=\psi(t)\end{cases}\;(\alpha\leqslant\theta\leqslant\beta)\, L:{x=φ(t)y=ψ(t)(α⩽θ⩽β)绕 x \,x\, x轴旋转所得旋转体的侧面积:
A = 2 π ∫ α β ∣ ψ ( t ) ∣ ⋅ φ ′ 2 ( t ) + ψ ′ 2 ( t ) d t {\color{Blue}A=2\pi\int^\beta_\alpha\big|\psi(t)\big|\cdot\sqrt{\varphi'^2(t)+\psi'^2{(t)}}\text{d}t} A=2π∫αβ∣∣ψ(t)∣∣⋅φ′2(t)+ψ′2(t)dt
(三) 体积
注意:求侧面积用 d s \,\text{d}s ds,求体积则用 d x \,\text{d}x dx.
1 绕 x \,x\, x轴旋转体
L : y = f ( x ) ( a ⩽ x ⩽ b ) L:y=f(x)\;(a\leqslant x\leqslant b)\, L:y=f(x)(a⩽x⩽b)与 x \,x\, x轴围成的图形绕 x \,x\, x轴旋转一周所得旋转体的体积:
V x = π ∫ a b f 2 ( x ) d x {\color{Blue}V_x=\pi\int^b_af^2(x)\text{d}x} Vx=π∫abf2(x)dx
2 绕 y \,y\, y轴旋转体
L : y = f ( x ) ( a ⩽ x ⩽ b ) L:y=f(x)\;(a\leqslant x\leqslant b)\, L:y=f(x)(a⩽x⩽b)与 x \,x\, x轴围成的图形绕 y \,y\, y轴旋转一周所得旋转体的体积:
V y = 2 π ∫ a b ∣ x ∣ ∣ f ( x ) ∣ d x {\color{Blue}V_y=2\pi\int^b_a\big|x\big|\big|f(x)\big|\text{d}x} Vy=2π∫ab∣∣x∣∣∣∣f(x)∣∣dx
3 截口面积求体积
几何体位于
x
=
a
\,x=a\,
x=a与
x
=
b
\,x=b\,
x=b之间,对
x
∈
[
a
,
b
]
\,x\in[a,b]
x∈[a,b],截口面积为
A
(
x
)
\,A(x)
A(x),则几何体的体积为:
V
=
∫
a
b
A
(
x
)
d
x
{\color{Blue}V=\int^b_aA(x)\text{d}x}
V=∫abA(x)dx
(四) 弧长
l = ∫ L d s l=\int_L\text{d}s l=∫Lds
以下弧长公式与弧微分的三种形式一一对应:
L
:
y
=
f
(
x
)
(
a
⩽
x
⩽
b
)
L:y=f(x)\;(a\leqslant x\;\leqslant b)
L:y=f(x)(a⩽x⩽b),则曲线
L
\,L\,
L的长度为:
l
=
∫
a
b
1
+
f
′
2
(
x
)
d
x
{\color{Blue}l=\int^b_a\sqrt{1+f'^2(x)}\text{d}x}
l=∫ab1+f′2(x)dx
L
:
{
x
=
φ
(
t
)
y
=
ψ
(
t
)
(
α
⩽
θ
⩽
β
)
L:\begin{cases}x=\varphi(t)\\y=\psi(t)\end{cases}\;(\alpha\leqslant\theta\leqslant\beta)
L:{x=φ(t)y=ψ(t)(α⩽θ⩽β),则曲线
L
\,L\,
L的长度为:
l
=
∫
α
β
φ
′
2
(
t
)
+
ψ
′
2
(
t
)
d
t
{\color{Blue}l=\int^\beta_\alpha\sqrt{\varphi'^2(t)+\psi'^2(t)}\text{d}t}
l=∫αβφ′2(t)+ψ′2(t)dt
L
:
r
=
r
(
θ
)
(
a
⩽
θ
⩽
b
)
L:r=r(\theta)\;(a\leqslant \theta\;\leqslant b)
L:r=r(θ)(a⩽θ⩽b),则曲线
L
\,L\,
L的长度为:
l
=
∫
α
β
r
2
(
θ
)
+
r
′
2
(
θ
)
)
d
θ
{\color{Blue}l=\int^\beta_\alpha\sqrt{r^2(\theta)+r'^2(\theta))}\text{d}\theta}
l=∫αβr2(θ)+r′2(θ))dθ
(五) 平均值
f ˉ = 1 b − a ∫ a b f ( x ) d x \bar{f}=\frac{1}{b-a}\int^b_af(x)\text{d}x fˉ=b−a1∫abf(x)dx
9 定积分的物理应用
(一) 变力沿直线做功
设
F
(
x
)
\,F(x)\,
F(x)为沿
x
\,x\,
x轴正向的变力,则物体从点
a
\,a\,
a移动到点
b
\,b\,
b所做的功为:
W
=
∫
b
a
F
(
x
)
d
x
W=\int^a_bF(x)\text{d}x
W=∫baF(x)dx
(二) 抽水做功
设一盛满水的容器截口面积为
A
(
x
)
\,A(x)
A(x),水面初始位于
x
=
a
\,x=a\,
x=a处,抽水后水面位于
x
=
b
\,x=b\,
x=b处,则抽水过程所做的功为:
W
=
ρ
g
∫
a
b
x
A
(
x
)
d
x
W=\rho g\int^b_axA(x)\text{d}x
W=ρg∫abxA(x)dx
注意:这类题目要根据情况适当建立坐标系.
功元素为: d W = ρ g x A ( x ) d x \text{d}W=\rho gxA(x)\text{d}x dW=ρgxA(x)dx,代表抽掉截口面积为 A ( x ) \,A(x) A(x),高度为 d x \,\text{d}x\, dx的水所做的功.
(三) 平板受到的(静)水压力
设一垂直浸没在水中的平板(上下边水平,左右边不规则),以平板上边方向建立
y
\,y\,
y轴,则其上下边与
y
\,y\,
y轴平行(
x
=
a
x=a
x=a、
x
=
b
x=b
x=b),左右边分别对应关于
x
\,x\,
x的函数
y
=
f
(
x
)
\,y=f(x)
y=f(x)、
y
=
g
(
x
)
y=g(x)
y=g(x),则平板一侧受到的压力为:
F
=
ρ
g
∫
a
b
x
[
f
(
x
)
−
g
(
x
)
]
d
x
F=\rho g \int^b_a x [f(x)-g(x)]\text{d}x
F=ρg∫abx[f(x)−g(x)]dx
力元素为: d F = ρ g x [ f ( x ) − g ( x ) ] d x \text{d}F=\rho g x [f(x)-g(x)]\text{d}x dF=ρgx[f(x)−g(x)]dx,代表深度为 x \,x x,高度为 d x \,\text{d}x\, dx的平板所受到的(水平)压力.
题型
1 概念和性质
(一) 判断原函数连续、可导性
(二) 比较定积分大小
思路:
(1) 积分区间相同,比较定积分的大小转化为比较被积函数的大小.
(2) 见到
(
b
−
a
)
\,(b-a)\,
(b−a)要能够熟练转换积分:
f
(
b
)
(
b
−
a
)
=
∫
a
b
f
(
b
)
d
x
f(b)(b-a)=\int^b_af(b)\text{d}x
f(b)(b−a)=∫abf(b)dx,便于比较.
(三) 积分中值定理
(四) 求平均值
y = f ( x ) ( a ⩽ x ⩽ b ) ⇒ y ˉ = 1 b − a ∫ a b f ( x ) d x y=f(x)\;(a\leqslant x\leqslant b)\Rightarrow\bar{y}=\frac{1}{b-a}\int^b_af(x)\text{d}x y=f(x)(a⩽x⩽b)⇒yˉ=b−a1∫abf(x)dx
2 定积分定义求n项和极限
极限与连续部分的重复考点,不再赘述.
3 由 f ( x ) \,f(x)\, f(x)含自身定积分的表达式,求 f ( x ) \,f(x) f(x) (设 A \,A A)
思路:
设
A
=
\,A=\,
A=式中出现的定积分.
例:
f ( x ) = x 1 + cos 2 x + ∫ − π π f ( x ) sin x d x , f ( x ) = ? f(x)=\frac{x}{1+\text{cos}^2x}+\int^{\pi}_{-\pi}f(x)\text{sin}x\text{d}x,f(x)=? f(x)=1+cos2xx+∫−ππf(x)sinxdx,f(x)=?
解:
1 o 1^o\; 1o设 A = ∫ − π π f ( x ) sin x d x \,A=\int^{\pi}_{-\pi}f(x)\text{sin}x\text{d}x A=∫−ππf(x)sinxdx, 则有
f ( x ) sin x = x sin x 1 + cos 2 x + A ⋅ sin x f(x)\text{sin}x=\frac{x\text{sin}x}{1+\text{cos}^2x}+A\cdot\text{sin}x f(x)sinx=1+cos2xxsinx+A⋅sinx
2 o 2^o\; 2o两边求积分:
A = ∫ − π π x sin x 1 + cos 2 x d x = − 2 π ∫ 0 π 2 d ( cos x ) 1 + cos 2 x = π 2 2 A=\int_{-\pi}^{\pi}\frac{x\text{sin}x}{1+\text{cos}^2x}\text{d}x=-2\pi\int^{\frac{\pi}{2}}_0{\frac{\text{d}(\text{cos}x)}{1+\text{cos}^2x}}=\frac{\pi^2}{2} A=∫−ππ1+cos2xxsinxdx=−2π∫02π1+cos2xd(cosx)=2π2
3 o 3^o\; 3o带回 f ( x ) \,f(x)\, f(x)表达式:
f ( x ) = x 1 + cos 2 x + π 2 2 . f(x)=\frac{x}{1+\text{cos}^2x}+\frac{\pi^2}{2}. f(x)=1+cos2xx+2π2.
注意:如果一个等式出现多个不同积分限,要依次设 A \,A A、 B B B、…求解.
4 变积分限函数相关问题
注意:不管是哪种变积分限的问题,都必先清理变积分限变量,再进行计算.
(1) 求导数
(2) 求极限
清理积分限变量、洛必达法则、构造导数定义 (可能是莱布尼茨公式形式),无非就是这些考法.
(3) 计算定积分
(4) 求最值
(5) 周期函数性质
(6) 判断奇偶性
(7) 判断正负
(8) 判断等价无穷小
(9) 结合二重积分
(10) 结合微分方程
(11) 确定原函数
5 定积分的计算
(1) 特殊性质计算定积分
包括三类:对称区间的定积分性质、三角函数的定积分性质、周期函数定积分性质,解法见记忆内容部分.
(2) 积分法计算定积分
主要是通过换元积分法、分部积分法,或根据几何意义求解.
注意:有一类题型需要特别留意:
题目给出一个变积分限函数
f
(
x
)
\,f(x)\,
f(x)(但它往往积不出来)或者给出一些
f
(
x
)
\,f(x)\,
f(x)的定积分条件,然后要求计算另一个含
f
(
x
)
\,f(x)\,
f(x)的积分. 这种题目需从结论入手,使用分部积分法解决.
(3) 分段函数计算定积分
注意:
(1) 分段函数题目也常与变积分限函数结合. 有的题目要求的是变积分限函数
F
(
x
)
=
∫
0
x
f
(
t
)
d
t
F(x)=\int^x_0f(t)\text{d}t
F(x)=∫0xf(t)dt,注意段与段之间存在"累积"效果. 比如
x
∈
[
0
,
2
]
\,x\in[0,2]
x∈[0,2],计算
1
<
x
⩽
2
\,1<x\leqslant2\,
1<x⩽2这段的
F
(
x
)
\,F(x)\,
F(x)时,不要忘记加上
0
<
x
⩽
1
\,0<x\leqslant 1\,
0<x⩽1这段,即
F
(
x
)
=
∫
0
1
+
∫
1
x
\,F(x)=\int_0^1+\int_1^x\,
F(x)=∫01+∫1x.
(2) 绝对值、
max
\text{max}
max、
min
\text{min}
min、数列极限等都是分段函数的标志.
(4) 积分限变换计算定积分
这些题目没有总结出特殊性质 (比如 tan x \,\text{tan}x\, tanx和 cot x \,\text{cot}x\, cotx之间的转换),但使用积分限变换的一些技巧也能求解 (记忆内容部分有总结).
6 定积分证明
(一) f ( x ) f(x)\, f(x)为连续函数
特征:只给了连续(或可积)条件和其他初始条件,没有涉及任何导数.
解题思路:
这类题目五花八门,不便总结,下面列举可能使用到的一些方法:
(1) 基本性质、特殊性质等;
(2) 变换积分区间;
(3) 定积分遇到绝对值的处理;
(4) 定积分和非定积分组成式子的处理;
(5) 定积分相关不等式性质;
(6) 积分中值定理(闭区间)、对原函数使用中值定理(开区间);
(7) 柯西不等式;
注意:
构造辅助函数发现取不到端点的处理方法:
比如使用还原法构造出辅助函数:
φ
(
x
)
=
∫
0
x
f
(
x
)
d
x
x
\varphi(x)=\frac{\int^x_0f(x)\text{d}x}{x}
φ(x)=x∫0xf(x)dx
题目中条件为
f
(
0
)
=
0
f(0)=0
f(0)=0,
∫
0
1
f
(
x
)
d
x
=
0
\int^1_0f(x)\text{d}x=0
∫01f(x)dx=0,显然我们希望
φ
(
0
)
=
φ
(
1
)
=
0
\,\varphi(0)=\varphi(1)=0
φ(0)=φ(1)=0.
然而
φ
(
x
)
\,\varphi(x)\,
φ(x)在
x
=
0
\,x=0\,
x=0点不存在.
因此我们重新构造辅助函数为:
φ
(
x
)
=
{
∫
0
x
f
(
x
)
d
x
x
,
0
<
x
⩽
1
0
,
x
=
0.
\varphi(x)=\begin{cases}\frac{\int^x_0f(x)\text{d}x}{x},&0<x\leqslant 1\\0,&x=0.\end{cases}
φ(x)={x∫0xf(x)dx,0,0<x⩽1x=0.
(二) f ( x ) f(x)\, f(x)为连续函数且 f ( x ) \,f(x)\, f(x)单调增加/减少
特征:只给了连续条件和单调性,以及其他初始条件,没有涉及任何导数.
思路:
1. 利用基本性质、特殊性质、变换积分限等;
2. 根据单调性构造辅助函数,主要有两种方法:
(1) 若结论是关于
a
\,a
a、
b
\,b\,
b的定积分等式或不等式,
φ
(
x
)
=
\varphi(x)=\,
φ(x)=左侧
−
\,-\,
−右侧 (将
b
\,b\,
b改为
x
\,x
x).
(2) 若
f
(
x
)
\,f(x)\,
f(x)单调增加,则
∀
x
,
y
∈
[
a
,
b
]
\,\forall\,x,y\in[a,b]
∀x,y∈[a,b],
(
x
−
y
)
[
f
(
x
)
−
f
(
y
)
]
⩾
0
(x-y)[f(x)-f(y)]\geqslant0
(x−y)[f(x)−f(y)]⩾0;
若
f
(
x
)
\,f(x)\,
f(x)单调减少,则
∀
x
,
y
∈
[
a
,
b
]
\,\forall\,x,y\in[a,b]
∀x,y∈[a,b],
(
x
−
y
)
[
f
(
x
)
−
f
(
y
)
]
⩽
0
(x-y)[f(x)-f(y)]\leqslant0
(x−y)[f(x)−f(y)]⩽0.
构造辅助函数时,要从结论中选取两个点作为
x
\,x\,
x和
y
\,y\,
y (通常是
x
\,x\,
x和另一个点).
3. 积分中值定理.
(三) f ( x ) f(x)\, f(x)为周期函数
思路:使用周期函数的两个性质.
注意:
1. 要熟练辨别周期函数,题目通常不会直接明示;
2. 要非常熟练运用两个性质,尤其是二者的结合使用:
∫
0
n
π
∣
cos
x
∣
d
x
=
n
∫
0
π
∣
cos
x
∣
d
x
=
n
∫
−
π
2
π
2
∣
cos
x
∣
d
x
=
2
n
∫
0
π
2
cos
x
d
x
=
2
n
\int^{n\pi}_0\big|\text{cos}x\big|\text{d}x=n\int^{\pi}_0\big|\text{cos}x\big|\text{d}x=n\int^{\frac{\pi}{2}}_{-\frac{\pi}{2}}\big|\text{cos}x\big|\text{d}x=2n\int^{\frac{\pi}{2}}_0\text{cos}x\text{d}x=2n
∫0nπ∣∣cosx∣∣dx=n∫0π∣∣cosx∣∣dx=n∫−2π2π∣∣cosx∣∣dx=2n∫02πcosxdx=2n
3. 对 ∀ x \;\forall\,x ∀x,都存在自然数 n \,n\, n,使得 n T ⩽ x ⩽ ( n + 1 ) T \,nT\leqslant x\leqslant(n+1)T nT⩽x⩽(n+1)T.
(四) f ( x ) f(x)\, f(x)在 [ a , b ] \,[a,b]\, [a,b]上一阶可导
思路:中值定理重复考点,不多赘述,特别强调
f
\,f
f、
f
′
f'\,
f′问题的解题思路:
题干中只涉及
f
\,f
f、
f
′
f'\,
f′:
(1) 有单调性条件:
f
′
>
0
(
<
0
)
⇒
f
↑
(
↓
)
f'>0\;(<0)\Rightarrow f\uparrow\;(\downarrow)
f′>0(<0)⇒f↑(↓);
(2) 待证结论积分号中无导数 (
L
\text{L}
L):
f
(
x
)
−
f
(
a
)
=
f
′
(
ξ
)
(
x
−
a
)
f(x)-f(a)=f'(\xi)(x-a)
f(x)−f(a)=f′(ξ)(x−a);
(3) 待证结论积分号中有导数 (
N
.
−
L
.
N.-L.
N.−L.):
f
(
x
)
−
f
(
a
)
=
∫
a
x
f
′
(
t
)
d
t
f(x)-f(a)=\int^x_af'(t)\text{d}t
f(x)−f(a)=∫axf′(t)dt.
注意:
(1) 待证结论出现复杂的最值表示形式 (如:
max
0
⩽
x
⩽
1
∣
f
′
(
x
)
∣
d
x
\max\limits_{0\leqslant x\leqslant 1}|f'(x)|\text{d}x
0⩽x⩽1max∣f′(x)∣dx),可以令其等于
m
\,m
m、
M
M
M,便于分析.
(2) 关于什么时候应该设
F
(
x
)
\,F(x)
F(x):
a. 题干出现
∫
a
b
f
(
x
)
d
x
=
0
\,\int_a^bf(x)\text{d}x=0
∫abf(x)dx=0:
F
(
a
)
=
F
(
b
)
=
0
F(a)=F(b)=0
F(a)=F(b)=0.
(五) f ( x ) f(x)\, f(x)高阶可导
思路:
1. 涉及定积分的高阶导数问题,多半使用
T
\,\text{T}\,
T. 关于
x
0
\,x_0\,
x0与
ξ
\,\xi\,
ξ的选取同中值定理的选取,不再赘述. 但泰勒公式使用函数可能是
f
(
x
)
\,f(x)\,
f(x)或
F
(
x
)
\,F(x)\,
F(x).
当出现以下两种情况时,考虑对
F
(
x
)
\,F(x)\,
F(x)使用
T
\,\text{T}
T:
(1) 待证结论中出现
ξ
∈
(
a
,
b
)
\,\xi\in(a,b)
ξ∈(a,b).
(2) 待证结论中出现
f
(
n
)
(
ξ
)
(
n
+
1
)
!
\,\frac{f^{(n)}(\xi)}{(n+1)!}
(n+1)!f(n)(ξ).
2. 关于
f
′
′
(
x
)
⩾
0
(
⩽
0
)
\,f''(x)\geqslant 0\,(\leqslant 0)\,
f′′(x)⩾0(⩽0)的两个思路:
(1)
f
′
(
x
)
↑
f'(x)\uparrow
f′(x)↑;
(2)
f
(
x
)
⩾
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
f(x)\geqslant f(x_0)+f'(x_0)(x-x_0)
f(x)⩾f(x0)+f′(x0)(x−x0).
(六) 疑难题目总结
(1) 题目要证明或求 lim x → 0 ∫ 0 x f ( t ) d t x \lim\limits_{x\to0}\frac{\int^x_0f(t)\text{d}t}{x} x→0limx∫0xf(t)dt
题目特征:
这类题目会显式或隐式的告知函数
f
(
x
)
\,f(x)\,
f(x)是周期函数. 最后要求解出
lim
x
→
0
∫
0
x
f
(
t
)
d
t
x
\,\lim\limits_{x\to0}\frac{\int^x_0f(t)\text{d}t}{x}\,
x→0limx∫0xf(t)dt或证明
lim
x
→
0
∫
0
x
f
(
t
)
d
t
x
=
.
.
.
\,\lim\limits_{x\to0}\frac{\int^x_0f(t)\text{d}t}{x}=...
x→0limx∫0xf(t)dt=...,基本按照下面的固定套路求解. 难题可能会在判断
f
(
x
)
\,f(x)\,
f(x)是周期函数和确定其周期上做文章.
解题步骤:
- 确定函数是周期函数 (确定周期为 T \,T T),确定函数大于等于 0 \,0\, 0还是小于等于 0 \,0 0.
- 对 ∀ x \;\forall\,x ∀x,都存在自然数 n \,n\, n,使得 n T ⩽ x ⩽ ( n + 1 ) T \,nT\leqslant x\leqslant(n+1)T nT⩽x⩽(n+1)T.
- 根据函数正负得到下面的关系 (以
f
(
x
)
⩾
0
\,f(x)\geqslant 0\,
f(x)⩾0为例):
∫ 0 n f ( x ) d x ⩽ ∫ 0 x f ( x ) d x ⩽ ∫ 0 n + 1 f ( x ) d x \int^n_0f(x)\text{d}x\leqslant\int^x_0f(x)\text{d}x\leqslant\int^{n+1}_0f(x)\text{d}x ∫0nf(x)dx⩽∫0xf(x)dx⩽∫0n+1f(x)dx
n ∫ 0 1 f ( x ) d x ⩽ ∫ 0 x f ( x ) d x ⩽ ( n + 1 ) ∫ 0 1 f ( x ) d x n\int^1_0f(x)\text{d}x\leqslant\int^x_0f(x)\text{d}x\leqslant(n+1)\int^{1}_0f(x)\text{d}x n∫01f(x)dx⩽∫0xf(x)dx⩽(n+1)∫01f(x)dx
-
由 n T ⩽ x ⩽ ( n + 1 ) T \,nT\leqslant x\leqslant(n+1)T nT⩽x⩽(n+1)T,
n ∫ 0 1 f ( x ) d x ( n + 1 ) T ⩽ ∫ 0 x f ( x ) d x x ⩽ ( n + 1 ) ∫ 0 1 f ( x ) d x n T \frac{n\int^1_0f(x)\text{d}x}{(n+1)T}\leqslant\frac{\int^x_0f(x)\text{d}x}{x}\leqslant\frac{(n+1)\int^{1}_0f(x)\text{d}x}{nT} (n+1)Tn∫01f(x)dx⩽x∫0xf(x)dx⩽nT(n+1)∫01f(x)dx -
运用夹逼定理求极限,这种题目左右侧极限必然是等于同一个值的.
(2) 条件出现 0 < m ⩽ f ( x ) ⩽ M \,0<m\leqslant f(x)\leqslant M 0<m⩽f(x)⩽M
可以考虑下面的一系列处理思路 (当然有的题目不需要进行完这个过程). 总之这种条件算是一种单调性条件的替换.
处理思路:
1.
0
<
m
⩽
f
(
x
)
⩽
M
⇒
f
(
x
)
−
M
⩽
0
0<m\leqslant f(x)\leqslant M\Rightarrow f(x)-M\leqslant 0
0<m⩽f(x)⩽M⇒f(x)−M⩽0,
f
(
x
)
−
m
⩾
0
f(x)-m\geqslant 0
f(x)−m⩾0;
2. [ f ( x ) − m ] [ f ( x ) − M ] ⩽ 0 [f(x)-m][f(x)-M]\leqslant 0 [f(x)−m][f(x)−M]⩽0;
3.
[
f
(
x
)
−
m
]
[
f
(
x
)
−
M
]
f
(
x
)
⩽
0
\frac{[f(x)-m][f(x)-M]}{f(x)}\leqslant 0
f(x)[f(x)−m][f(x)−M]⩽0;
4.
f
(
x
)
+
m
M
f
(
x
)
⩽
m
+
M
f(x)+\frac{mM}{f(x)}\leqslant m+M
f(x)+f(x)mM⩽m+M;
(3) 定积分+非定积分的两种思路
在记忆部分中已经给出了处理思路,不再赘述.
(4) 柯西不等式
使用柯西不等式的特征:
1. 待证结论中出现定积分之积;
2. 待证结论中定积分内部出现平方.
(5) 拆分
注意:
(1) 柯西不等式的使用非常灵活,有的题目需要考虑引入:
∫
a
b
1
2
d
x
\int_a^b 1^2\text{d}x
∫ab12dx.
比如下面的不等式成立,即
g
(
x
)
=
1
\,g(x)=1
g(x)=1:
[
∫
a
b
f
(
x
)
d
x
]
2
⩽
∫
a
b
f
2
(
x
)
d
x
⋅
∫
a
b
1
2
d
x
\bigg[\int^b_af(x)\text{d}x\bigg]^2\leqslant \int_a^b f^2(x)\text{d}x\cdot\int_a^b 1^2\text{d}x
[∫abf(x)dx]2⩽∫abf2(x)dx⋅∫ab12dx
(2) 只要出现定积分之积就要考虑能不能使用柯西不等式解,即使没有平方也要考虑构造,比如:
∫
0
π
2
a
cos
x
d
x
⋅
∫
0
π
2
a
−
cos
x
d
x
=
∫
0
π
2
(
a
cos
x
2
)
2
d
x
⋅
∫
0
π
2
(
a
−
cos
x
2
)
2
d
x
\int^{\frac{\pi}{2}}_0a^{\text{cos}x}\text{d}x\cdot\int^{\frac{\pi}{2}}_0a^{-\text{cos}x}\text{d}x=\int^{\frac{\pi}{2}}_0(a^{\frac{\text{cos}x}{2}})^2\text{d}x\cdot\int^{\frac{\pi}{2}}_0(a^{-\frac{\text{cos}x}{2}})^2\text{d}x
∫02πacosxdx⋅∫02πa−cosxdx=∫02π(a2cosx)2dx⋅∫02π(a−2cosx)2dx
⩾
(
∫
0
π
2
a
cos
x
2
⋅
a
−
cos
x
2
d
x
)
2
=
π
2
4
\geqslant\bigg(\int^{\frac{\pi}{2}}_0a^{\frac{\text{cos}x}{2}}\cdot a^{-\frac{\text{cos}x}{2}}\text{d}x\bigg)^2=\frac{\pi^2}{4}
⩾(∫02πa2cosx⋅a−2cosxdx)2=4π2
(3) 不一定结论就可以直接往柯西不等式上套. 比如有的题目可能就需要先构造
f
(
x
)
\,f(x)\,
f(x)的平方,再两边积分才能使用柯西不等式.
(6) 变换积分区间
在记忆部分中已经给出了处理思路,不再赘述. 这类题目需要多练习,其中有些构造非常精巧.
(7) 定积分进入函数内部
题目特征:
待证结论中出现定积分在函数内部,通常需要用
f
′
′
(
x
)
\,f''(x)\,
f′′(x)的性质解决. 这类题目特征不太好描述,看两个例子感受吧.
比如证明的结论是:
ln
∫
0
1
f
(
x
)
d
x
=
∫
0
1
ln
f
(
x
)
d
x
\text{ln}\int_0^1f(x)\text{d}x=\int^1_0\text{ln}f(x)\text{d}x
ln∫01f(x)dx=∫01lnf(x)dx
f
[
∫
a
b
x
φ
(
x
)
d
x
]
⩽
∫
a
b
f
(
x
)
φ
(
x
)
d
x
f\big[\int^b_ax\varphi(x)\text{d}x\big] \leqslant\int_a^bf(x)\varphi{(x)}\text{d}x
f[∫abxφ(x)dx]⩽∫abf(x)φ(x)dx
解题思路:
- 确定函数 g ( x ) \,g(x) g(x). 即定积分外部的那个函数,比如上面的第1个例子 g ( x ) = ln t \,g(x)=\text{ln}t g(x)=lnt,第2个例子就是 f ( x ) \,f(x)\, f(x)本身)
- 确定 g ′ ′ ( x ) \,g''(x)\, g′′(x)正负 (假设 g ′ ′ ( x ) ⩾ 0 \,g''(x)\geqslant 0 g′′(x)⩾0). 有的题目会直接给出,有的题目需要自己求.
- 令 x 0 = \,x_0=\, x0=出现在 g ( x ) \,g(x)\, g(x)内部的定积分. 比如上面第1个例子 x 0 = ∫ 0 1 f ( x ) d x \,x_0=\int^1_0f(x)\text{d}x x0=∫01f(x)dx,第2个例子 x 0 = ∫ a b x φ ( x ) d x \,x_0=\int^b_ax\varphi(x)\text{d}x x0=∫abxφ(x)dx.
- 利用 g ( x ) ⩾ g ( x 0 ) + g ′ ( x 0 ) ( x − x 0 ) \,g(x)\geqslant g(x_0)+g'(x_0)(x-x_0) g(x)⩾g(x0)+g′(x0)(x−x0),推出不等关系.
7 反常积分计算
思路:
(1)
Γ
\Gamma\,
Γ函数计算.
(2) 判别法.
(3) 如果出现在填空题,不必浪费时间判断是否收敛.
























 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








