二维Winograd算法

 

Winograd算法：

该算法在多个相关论文中都被采用了，这里详细记录一下算法原理。

1D卷积：

输入向量：

输入卷积核：

输出向量：

卷积步长为1，输入向量d长度为4，卷积核长度为3，则输出向量长度为2。

采用普通卷积方式的卷积计算方式如下：

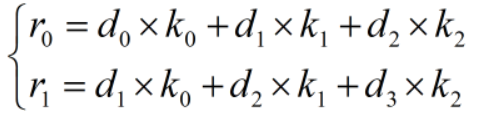
写成矩阵形式为：

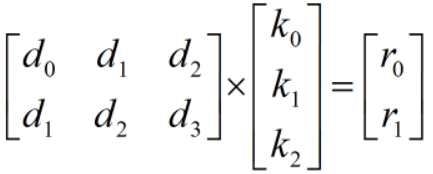
显而易见，普通卷积方式需要6次乘法和4次加法。

总结普通卷积的公式如下：

还没总结出来。。。。

1DWinograd算法：

这里只讨论使用方式，不讨论算法本身的推导。

首先将r0和r1拆分如下：

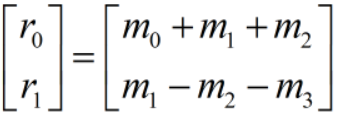
规定以下计算方式，使得最终结果与普通卷积相等：

 

由于在神经网络推理时，卷积核的值是固定的，所以可以通过预计算将涉及到k的乘法、加法、减法提前计算出来（实际操作中也可以做1/2也可以移位处理）。因此，通过这种拆分方式，计算出r0和r1只需要4次乘法和8次加减法。这样就非常有利于嵌入式平台的实现，这是因为在硬件中，加减法比乘法高效的多，且乘法器资源也是有限的，所以Winorad算法核心思想是用增加加减法次数的代价减少乘法的次数。

根据上述推导总结出1D Winograd卷积计算公式：

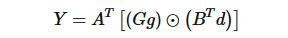
其中，G表示卷积核变换矩阵，表示输入变换矩阵，g为卷积核，d为输入向量，为输出变换矩阵，表示哈达玛积，即矩阵对应位置相乘。

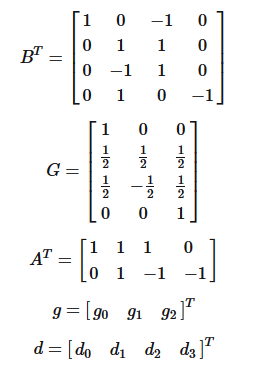
值得一提的是，虽然矩阵形式的卷积与Winograd算法等价，但是在矩阵形式中d是2个3维向量，Winograd算法中的d是4维向量。因此，从另一个角度来说，Winograd算法还有个好处是将输入向量从卷积的二维压到了一维，即可以将任意形如下式中输入排列的矩阵转换为一维输入。

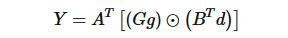
其中g为[x,y,x],d为[A,B,C,D]。

在实际工程中，必须要考虑到，Winograd虽然减少了乘法次数，但是增加了计算方式转换以及内存的要求。

2DWinograd算法：

考虑到实际应用单通道图片是2D维度，因此需要将Winograd算法从1D扩展至2D。

设输入图片尺寸为4x4：

卷积核尺寸为3x3：

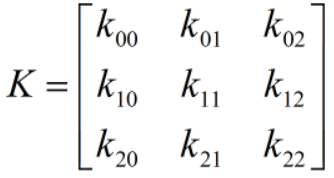
计算过程为：

将

那么对应输出矩阵的计算过程为：

 

仔细观察上述2D卷积过程，对输入矩阵和卷积核划分子矩阵，组织出1DWinograd结构：

 

即：

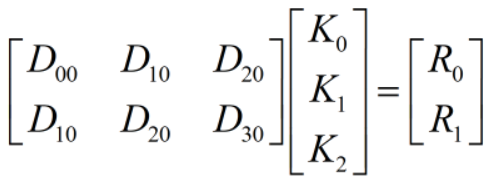
根据分块矩阵的性质，整体矩阵的相乘结果，与拆分成子矩阵后对应位置子矩阵的相乘结果一致（需要满足子矩阵的相乘是有意义的），那么就可以直接分块的子矩阵当成一般矩阵的元素处理，那么也就可以套用1DWinograd算法处理分块矩阵：

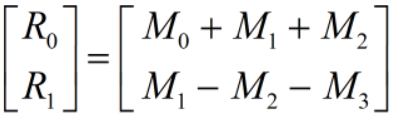
整理可得：

至此，推得二维Winograd公式。

参考：1.Winograd Convolution 推导 - 从1D到2D

          2.一维Winograd算法及其工程实现