贝叶斯信念网络

回顾

---

贝叶斯定理

贝叶斯定理是计算概率中很重要也是很常用的一个公式，它的形式如下：
$$p(Y_k|X)=\frac{P(X{Y}_k)}{P(X)}=\frac{P(Y_k)p(X|Y_k)}{{\sum }_{j}P(Y_j)P(X|Y_j)}$$

• $P(X)$：计算X的概率值
• $P(Y|X)$ :计算在输入为X的情况下结果为Y的条件概率值
• $P(XY)$：计算X和Y的联合概率分布

为什么要用到贝叶斯定理呢？是因为在实际中，当我们已有一系列的分类已知的数据时，我们很容易计算出当是某一类别Y时输入为Xi时的条件概率$P(X_i|Y)$，但是在得到一个新的 $X$时，我们不容易计算出$P(Y|X)$，这时就要借助贝叶斯公式来换个方向继续求解。

---

朴素贝叶斯（naïve bayes）

朴素贝叶斯算法是一种生成式方法，基于上面的贝叶斯定理和特征条件独立假设，广泛的用于一些分类问题。在朴素贝叶斯算法中，假设所有的数据都是独立同分布产生的，所以我们可以计算先验概率分布:
$$P(Y=c_k),k=1,2,...,K$$

和条件概率分布
$$P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=c_k)$$

进而求出数据集的联合概率分布$P(X,Y)$。

条件独立性假设是说在分类确定的情况下，输入是哪一个$X$时，彼此之间是互不影响的（它在朴素贝叶斯中是很重要的一个假设，大大的简化了算法的学习和预测）。数学表达如下所示：
$$P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=c_k)=\prod _{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k)$$
在求得先验分布和条件分布之后，我们就可以使用朴素贝叶斯对新的样本计算$P(Y|X)$ 来得到分类的结果。

另外，在实际采样得到的数据中，某些属性的值可能是没有的，为了避免这种情况对计算概率值时的影响，通常采用拉普拉斯修正（Laplacian correction）
$$p_{\lambda }(Y=c_k)=\frac{{\sum }_{i=1}^{N}I(y_i=c_k)+\lambda }{N+K\lambda }$$
其中$\lambda$ 是修正系数。

在引入拉普拉斯修正的朴素贝叶斯分类中存在着两个先验假设：

• 属性间彼此独立
• 属性值和类别均匀分布

---

半朴素贝叶斯分类器

但是在实际的应用中，朴素贝叶斯中引入先验假设往往很难满足，如果将其进行一定程度的放松，就得到一系列的半朴素贝斯分类器。

它的基本原理是只考虑某些属性之间的强的相互依赖，某些偌依赖就认为彼此是独立的。这样做既不必费时去计算完全概率分布，又不至于忽略某些属性之间的强相互依赖，一定程度上可以提升模型的泛化能力。

常见的方法有：ODE、SPODE、TAN、AODE……

---

贝叶斯信念网络

如果我们进一步的放宽对于假设的限制，考虑更多的属性之间的依赖关系，就可以得到下面要介绍的贝叶斯信念网络。

贝叶斯信念网络（或信念网）是一种经典的概率图模型，它主要包括如下两个部分：

• 有向无环图（DAG）：用来刻画属性之间的依赖关系
• 条件概率表（CPT）：用来描述属性的联合概率分布

贝叶斯网络有一条极为重要的性质，就是断言每一个节点在其直接前驱节点的值制定后，这个节点条件独立于其所有非直接前驱前辈节点。

一般情况下，如果多个变量之间不是相互独立的，那么它们组合的联合概率分布计算如下所示：
$$P(x_1,x_2,...,x_n)=P(x_1)P(x_2|x_1)P(x_3|x_1,x_2)...P(x_n|x_1,x_2,...,x_{n-1})$$
而在引入了上述的那条性质后，计算过程就可以简化成如下的形式：
$$P(x_1,x_2,...,x_n)=\prod _{i=1}^{n}P(x_i|Parent(x_i))$$
其中$Parent$ 表示$x_i$ 的直接前驱节点的联合。

下面我们通过一个例子来看一下贝叶斯信念网络。

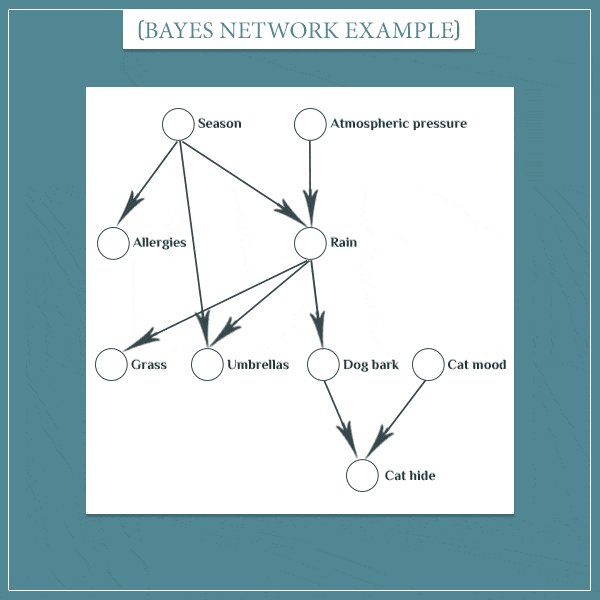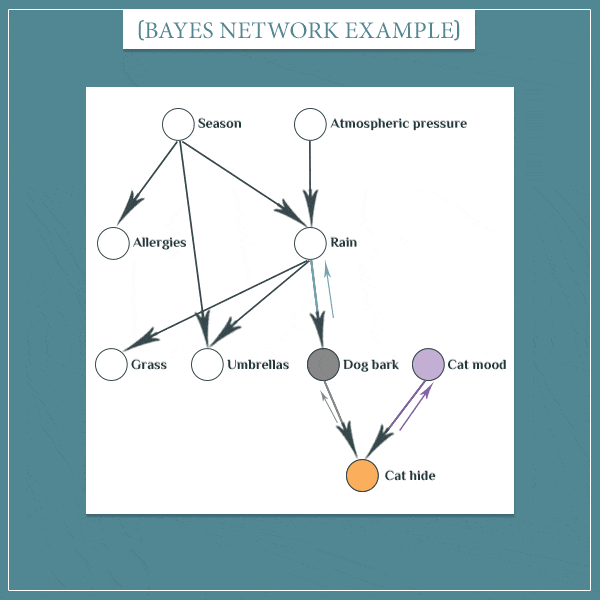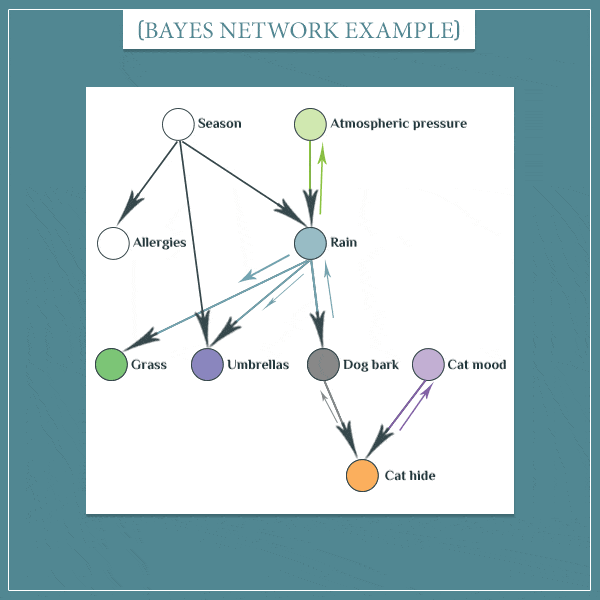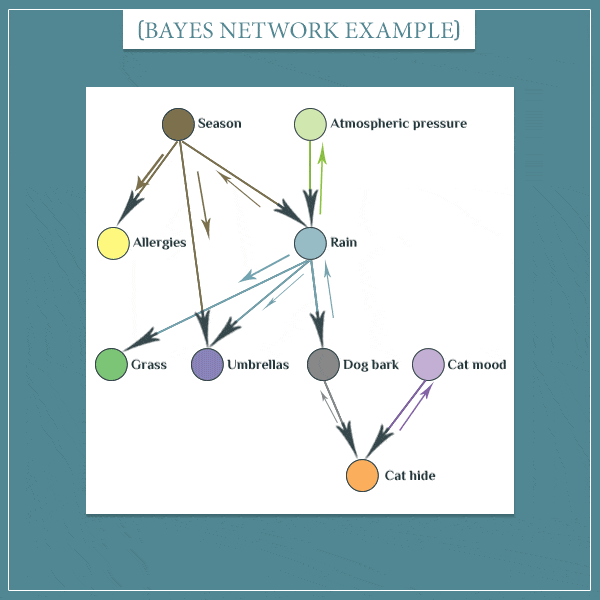
根据我们对于生活的观察可以得到一个如上所示的贝叶斯信念网络：季节和和大气压的情况会影响到是否会降雨；季节会影响一个人是否会发生过敏；是否下雨会影响到草地的状态、是否需要带伞、狗是否会叫；狗是否会叫以及猫的状态会影响它是否会藏起来（详情可见：What Are Bayesian Belief Networks? (Part 1）。

那么根据数据得到一个这样的信念网可以做什么呢？为了方便解释，我们以其中的一条路径来看
{ R a i n → [ D o g   b a r k ] + C a t   m o o d → C a t   h i d e } \{Rain \rightarrow [Dog\ bark]+Cat\ mood \rightarrow Cat\ hide \} {Rain→[Dog bark]+Cat mood→Cat hide}
其中每个节点的可能状态如下所示：

• Rain：Yes、No
• Dog bark：Yes、No
• Cat mood：Sleepy、Excited
• Cat hide：Yes、No

那么它们所对应的条件概率表示例如下所示：

Rain

	Rains	Doesn’t rain
P	12/48	36/48

Dog bark

	Rains	Doesn’t rain
Dog bark	9/48	18/48
Dog doesn’t bark	3/48	18/48

那么整个信念网联合分布如下所示
$$P(Network)=P(Season)\ast P(Atmosphericpressure)\ast P(Allergies|Season)\ast P(Rain|Season,Atmosphericpressure)\ast P(Grass|Rain)\ast P(Umbrellas|Season,Rain)\ast P(Dogbark|Rain)\ast P(Catmood)\ast P(Cathide|Dogbark,Catmood)$$

---

贝叶斯信念网络的训练

构造与训练贝叶斯网络分为以下两步（也就是说，给你一个训练元组，要用贝叶斯信念网络进行分类，需要做的事）：

1. 确定随机变量间的拓扑关系，形成DAG。这一步通常需要领域专家完成，而想要建立一个好的拓扑结构，通常需要不断迭代和改进才可以。

2. 训练贝叶斯网络。这一步也就是要完成条件概率表CPT的构造，这里又分为两种情况：

   • 如果每个随机变量的值都是可以直接观察的，直接计算CPT表目，方法类似于朴素贝叶斯分类
   • 如果贝叶斯网络中存在隐藏变量节点，那么训练方法就是比较复杂，例如可使用梯度下降法

下面主要来看一下使用梯度下降法如何训练贝叶斯信念网络。在此之前，作如下的规定：

• $D$：数据元组， D = { X 1 , X 2 , . . . , X ∣ D ∣ } D = \{ X_{1},X_{2},...,X_{|D|}\} D={X1​,X2​,...,X∣D∣​}
• $i$ : 表示节点的顺序，$Y_i$ 表示第$i$ 个节点代表的属性，例如$Y_i$ 代表$Dogbark$
• $j$ ：表示属性值的顺序，$y_{ij}$ 表示第$i$ 个节点取第$j$ 个属性的值，例如$y_{ij}$ 代表$Dogbark=True$
• $k$ ：直接前驱节点的顺序，$U_i$ 表示第$i$ 个节点的直接前驱节点，$u_{ik}$ 列出直接前驱节点的值，比如 U i = { D o g   b a r k , C a t   m o o d } U_{i} = \{ Dog\ bark,Cat\ mood\} Ui​={Dog bark,Cat mood} , U i k = { T r u e , E x c i t e d } U_{ik} = \{True,Excited\} Uik​={True,Excited} 。
• $w_{ijk}$ ：$w_{ijk}\equiv P(Y_i=y_{ij}|U_i=u_{ik})$ 表示CPT中的表目

梯度下降就是要迭代的搜索能最好的对数据建模的$w_{ijk}$ 的值。目标为最大化
$$P_w(D)=\prod _{d=1}^{|D|}{P}_w(x_d)$$
步骤如下：

• 计算梯度
  $$\frac{\partial P_w(D)}{\partial w_{ijk}}=\sum _{d=1}^{|D|}\frac{P(Y_i=y_{ij},U_i=u_{ij}|X_d)}{w_{ijk}}-$$

• 更新权重
  $$w_{ijk}\leftarrow w_{ijk}+l\frac{\partial P_w(D)}{\partial w_{ijk}}$$

• 重新规格化权重

  令$w_{ijk}$ 在0、1之间，且对所有的$i$ ,$k$ 使${\sum }_j{w}_{ijk}=1$

---

贝叶斯信念网的概率值更新

网络中关于一个或多个节点的信息的更新会影响每个节点上的概率分布。一般来说，信息在贝叶斯网络中有两种传播方式:预测（predictive）和回溯（retrospective）。

• Predictive
  如果有新的信息改变了一个节点的概率分布，该节点将把信息传递给它的子节点。孩子们将依次把信息传递给他们的孩子，以此类推。

  
  

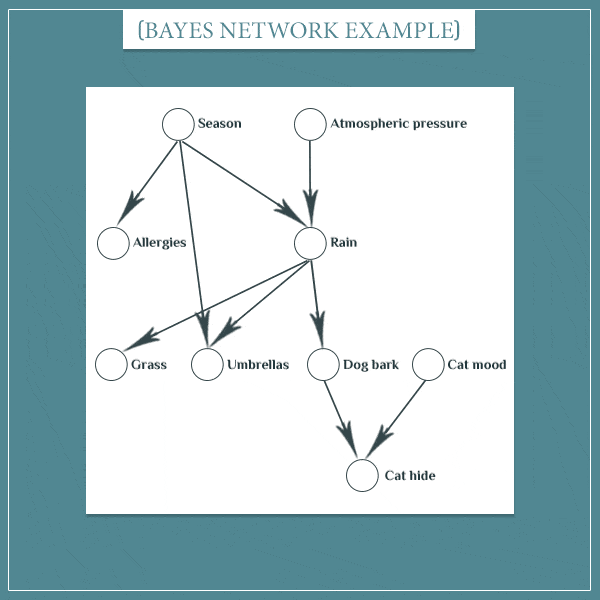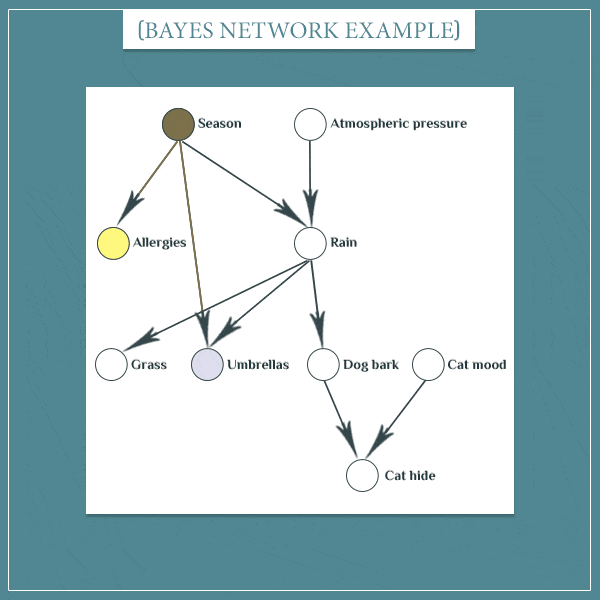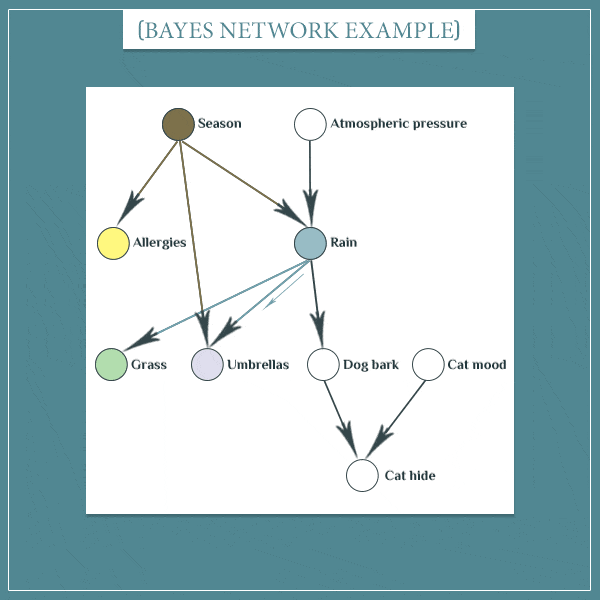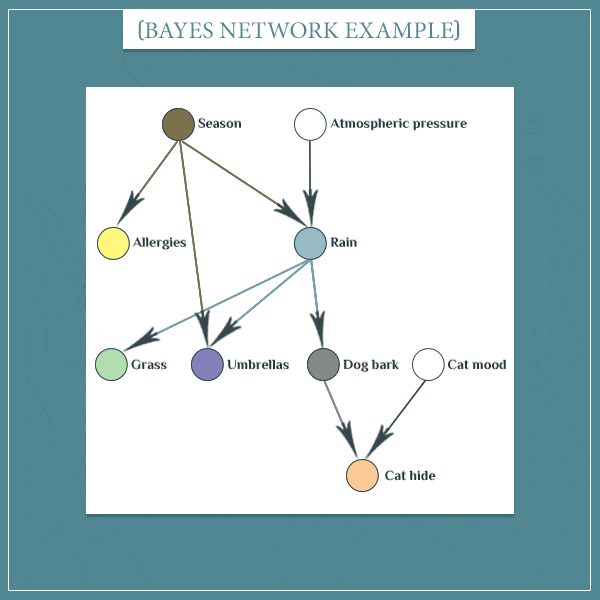
  假设当前的$P(Season=Fall)=1$，那么自然Season取其它的属性的概率值就为零。而$Season=Fall$ 又会提高$P(Rain=Yes)$ 的概率，接着同样会增加$P(Dogbark)$ 的概率，最后增加了$P(Cathide)$ 的概率。其他节点的更新同理。

• retrospective
  retrospective基本上与predictive相反。通常，当更新节点的概率分布时，节点也更新其子节点。但是，如果节点是直接更新的，或者由其子节点更新的，那么它也会更新其父节点。

  
  

  假设$P(Cathide=True)=1$ ，首先，知道猫在沙发下会改变“猫的情绪”和“狗叫”节点的概率。人们的直觉是，两者都可能是猫躲起来的原因。新更新的“Dog bark”节点现在将更新它自己的父节点“Rain”节点。

  注意，每个更新的节点还通过预测传播更新其子节点。例如，当“Dog bark”节点更新“Rain”节点时，后者更新“Grass”和“umbrella”节点。也就是说，现在P(Rain = True)更高，更有可能是草地湿了，人们带着雨伞。

  同样重要的是，当您更新两个或多个节点时，它们将同时更新它们的子节点(类似于一个节点如何同时更新其父节点)

---

优点

• 贝叶斯网络最强大之处在于从每个阶段结果所获得的概率都是数学与科学的反映（例如，分类时，贝叶斯网络返回的不是类标号，而是返回概率分布，给出每个类的概率），换句话说，假设我们了解了足够多的信息，根据这些信息获继而得统计知识，网络就会告诉我们合理的推断。

• 贝叶斯网络最很容易扩展(或减少,简化),以适应不断变化的需求和变化的知识

---

参考：

周志华 《?书》

韩家炜等 《数据挖掘-概念与技术》

分类算法之贝叶斯网络

贝叶斯信念网络

从贝叶斯方法谈到贝叶斯网络

What Are Bayesian Belief Networks? (Part 1)

What Are Bayesian Belief Networks? (Part 2)

An introduction to Bayesian Belief Network

A. Introduction to Bayes Nets