GAMES102几何建模与处理（一）

一、函数拟合

1、函数的集合

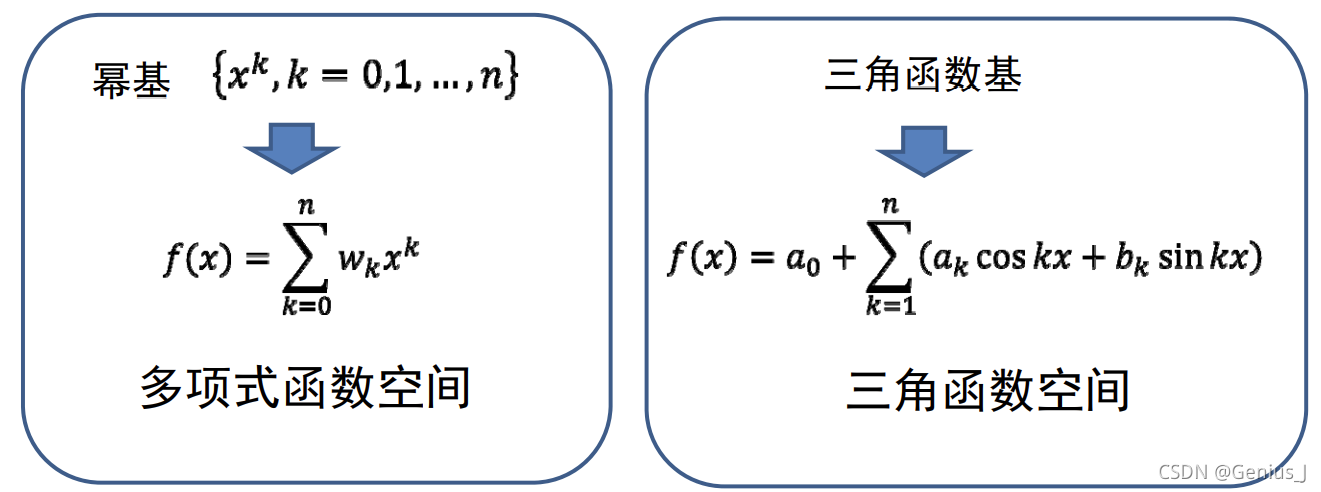
用若干简单函数（“基函数”）线性组合张成一个函数空间

• L = s p a n { f 1 , f 2 , … , f n } = ∑ i = 1 n a i f i ( x ) ∣ a i ∈ R L=span\{f_1,f_2,\dots,f_n \}=\sum^n_{i=1}a_if_i(x)|a_i\in R L=span{f1​,f2​,…,fn​}=∑i=1n​ai​fi​(x)∣ai​∈R
• 每个函数就表达（对应）为n个实数，即系数向量（$a_1,a_2,a_3,\dots ,a_n$）
• 空间的完备性：这个函数空间是否可以表示（逼近）任何函数
• 

2、赋范空间

• 内积诱导范数、距离
  $-<f,g>={\int }_a^{b}f(x)g(x)dx$
• 度量空间：可度量函数之间的距离。
  Lp范数
• 赋范空间+完备性=巴拿赫空间
• 内积空间（无限维）+完备性=希尔伯特空间

3、万能逼近定理

Weierstrass逼近定理

• 定理1：闭区间上的连续函数可用多项式级数一致逼近
• 定理2：闭区间上周期为2π的连续函数可用三角函数级数一致逼近
• 对于[a,b]上的任意连续函数g，及任意给定的$\xi >0$，必存在n次代数多项式$f(x)={\sum }_{k=0}^n{w}_k{x}^k$，使得
  $$mi{n}_{x\in [a,b]}|f(x)-g(x)|<\xi$$

4、函数复合

5、如何求满足要求的函数？

• 大部分的实际应用问题
  1、可建模为：找一个映射/变换/函数
  2、输入不一样、变量不一样、维数不一样
• 如何找函数的三步曲：
  1、到哪找？
  确定某个函数集合/空间
  2、 找哪个？
  度量哪个函数是好的/“最好”的
  3、怎么找？
  求解或优化：不同的优化方法与技巧，既要快、又要好

二、数据拟合

• 拟合问题
  输入：一些观察的数据点
  输出：反映这些数据规律的函数$y=f(x)$

1、 到哪找？

1、选择一个函数空间

• 线性函数空间 A = s p a n { B 0 ( x ) , … , B n ( x ) } A=span\{B_0(x),\dots,B_n(x)\} A=span{B0​(x),…,Bn​(x)}
  1、多项式函数 s p a n { 1 , x , x 2 , … , x n } span\{1,x,x^2,\dots,x^n\} span{1,x,x2,…,xn}
  2、RBF函数
  3、三角函数

2、函数表达

$f(x)={\sum }_{k=0}^n{B}_k(x)$
求n+1个系数$(a_0,\dots ,a_n)$(待定系数)

2、找哪个？

1、目标一：函数经过每个数据点（插值）

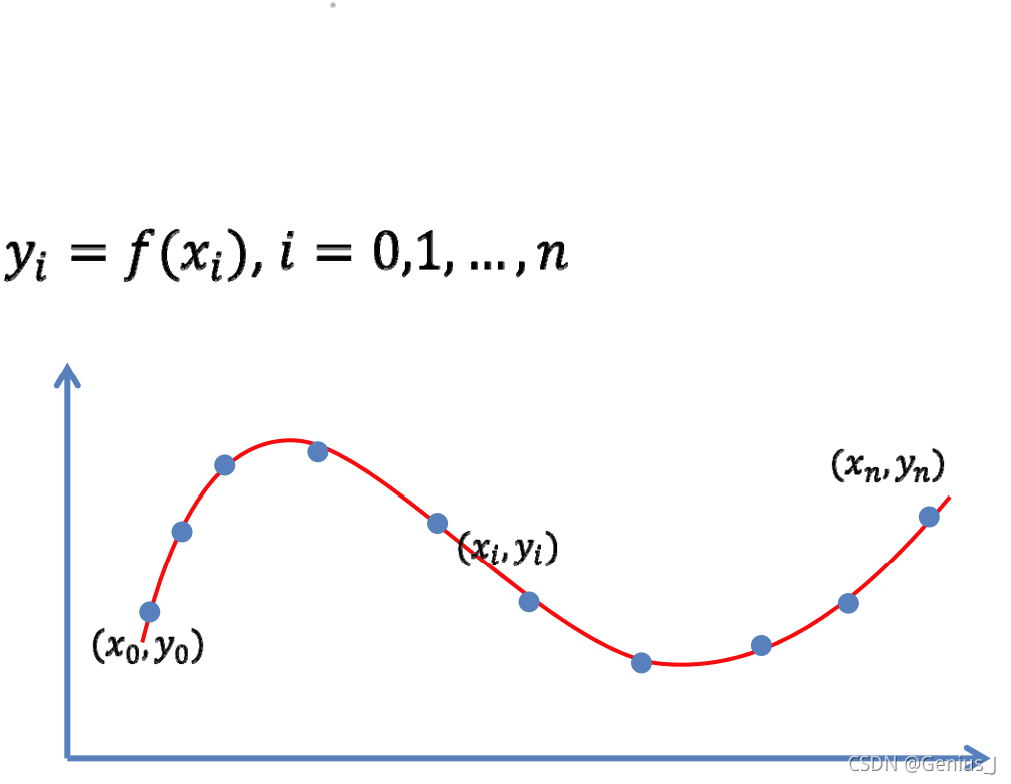
2、目标二：函数尽量靠近数据(逼近)

$min{\sum }_{i=0}^n(y_i-f(x_i){)}^2$

3、怎么找？

1、目标一：每一个数据点都要插值（零误差）

• 联立，求解线性方程组。
  ${\sum }_{k=0}^n{a}_k{B}_k(x_i)=y_i,i=0,1,\dots ,n$
  • 求解$(n+1)\times (n+1)$线性方程组
  • n次拉格朗日插值多项式
    病态问题：系数矩阵条件数高时，求解不稳定
• 拉格朗日插值多项式
  插值n+1个点、次数不超过n的多项式是存在而且是唯一的
  （n+1个变量，n+1个方程)
  $$p_k(x)=\prod _{i\in B_k}\frac{x-x_i}{x_k-x_i}$$
  插值函数的自由度=未知量个数-已知量个数

2、目标二：函数尽量靠近数据(逼近)

$min{\sum }_{i=0}^n(y_i-f(x_i){)}^2$
对各系数求导，得法方程（线性方程组）
$AX=b$ （最小二乘）
可能存在问题：
1、点多，系数少？
2、点少，系数多？

4、遇到的问题

1、过拟合

• 误差为0，但是拟合的函数并无使用价值
  

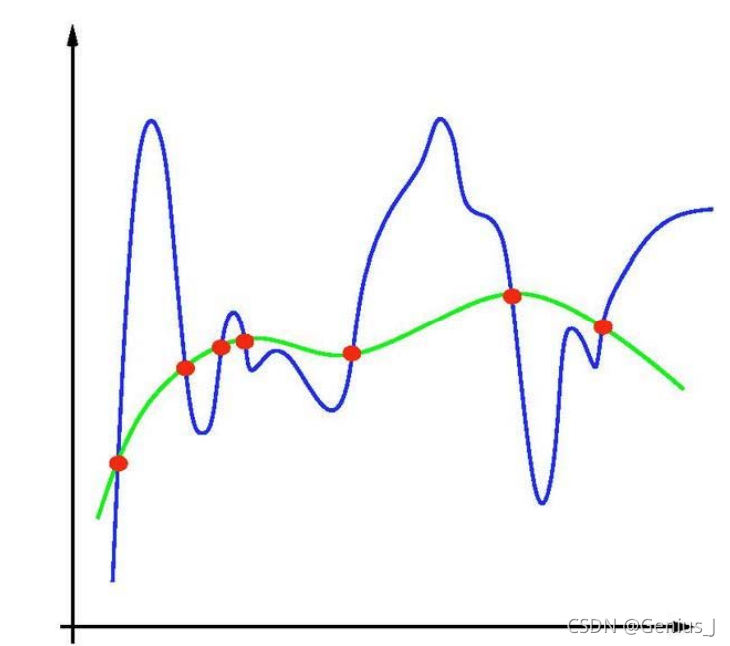
2、欠拟合

• 拟合程度不高，数据距离拟合曲线较远

3、常用解决方法

• 数据去噪
  剔除训练样本中的噪声
• 数据增广
  增加样本数，或者增加样本的代表性和多样性
• 模型简化
  1、预测模型过于复杂，拟合了训练样本中的噪声
  2、选用更简单的模型，或者对模型进行裁剪
• 正则约束
  适当的正则项，比如方差正则项、稀疏正则项

4、例子

• 岭回归正则项
  1、选择一个函数空间
  基函数的线性表达：$W=(w_0,w_1,\dots ,w_n)$
  $y={\sum }_{i=0}^n{w}_i{B}_i(x)$
  • 最小二乘拟合
    $mi{n}_w||Y-XW|{|}^2$
  • 岭回归
    $mi{n}_w||Y-XW|{|}^2+\mu ||W|{|}_2^2$
• 稀疏学习：稀疏正则化
  • 冗余基函数（过完备）
  • 通过优化来选择合适的基函数
    – 系数向量的$L_0$模（ 非0元素个数）尽量小
    – 挑选（“学习”）出合适的基函数
    $mi{n}_w||Y-XW|{|}^2+\mu ||W|{|}_0$
    $mi{n}_w||Y-XW|{|}^2,s.t.||W|{|}_0<\beta$
• 压缩感知
  • 已知y和Φ ，有无穷多解x
  • 对于稀疏信号x，可通过优化能完全重建x
    $min||x|{|}_0,s.t.\Phi x=y$
    
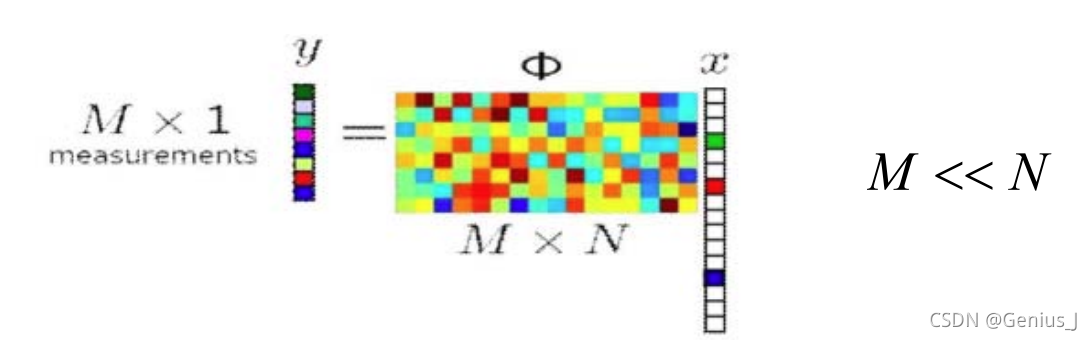
    – 在一定条件下 (on Φ)

三、参考和引用

[1] bilibili：GAMES102:几何建模与处理
[2] 数据拟合.pdf