GAMES102

1. 数据拟合

1.1 多项式插值

1.1.1 多项式插值的问题

多元函数张量积

两个变量的基函数可以不一样，但一般情况下，我们使用相同的基函数。

神经网络表达

向量值函数

变量x是一维的实数，它对应Rᵐ 空间的一条曲线。

参数方程？

低维->高维

u，v是上图的本质维度（二维）；

流形：R³上任意一点（无穷小的区域）等价于R²上的一个圆盘区域。

高维->低维

一般会伴有信息的丢失（高维->低维->高维，无法恢复）。

如果映射的特征维度低于本质维度，则无法恢复。

如上图中的曲面，该曲面上面的点的本质维度为2维，特征维度为3维，如果进行降维映射，再进行升维映射，可以恢复；但如果将该曲面进行降维映射，降到一维，再升到三维后会丢失信息。

总结：

曲线拟合

对于曲线拟合问题，可以将问题分解为：

①求出x和t的对应关系，拟合(t,x)     ②求出y和t的对应关系，拟合(t,y)

所以关键问题是找出曲线上的每个点(xᵢ ,yᵢ )对应的一维上的 tᵢ 。

参数化方法

3. 三次样条函数

3次多项式的性质和求解

 

数值计算 数值分析 4《Hermite插值多项式》埃尔米特插值多项式 期末不挂科_哔哩哔哩_bilibili

三次基样条

参数连续性

 

几何连续性

4. 贝塞尔曲线

n次Bezier曲线：n+1个控制顶点（0,1,...,n）。

Bernstein基函数

由性质1可知，贝塞尔曲线具有凸包性。

性质3：递推性

在左图中，由四个控制点生成的贝塞尔曲线经过升阶后（五个控制点），贝塞尔曲线不变。

de Casteljau算法

b₀³左边的曲线可以由控制点b₀⁰、b₀¹、b₀²和b₀³生成；

b₀³右边的曲线可以由控制点b₃⁰、b₂¹、b₁²和b₀³生成。

B样条

B样条曲线原理演示_哔哩哔哩_bilibili

基函数的性质：

①当tᵢ<t<tᵢ₊ₖ时，Nᵢ,k(t)>0，否则Nᵢ,ₖ(t)=0，如上图N₁,₃，当t∈(t₁,t₁₊₃)时，N₁,₃>0。

阶数k代表跨度。

②权性。

③Nᵢ,ₖ(t)在连接点tⱼ处为Cᵏ⁻²连续。

B样条曲线

性质：

①增加结点的重数会降低曲线的光滑度

②改变某个内部结点的位置之后影响一定范围的曲线，不会全局改变

B样条曲线的局部性表现：

曲线光顺

曲率：

①与参数化无关

②衡量曲线的弯曲程度

曲线的光顺：

对比上图中的图一和图二，以及图三和图四，我们很难区别出两条曲线有什么不同，但将曲线的曲率表示出来后，我们发现图二和图四的曲率变化较小，几乎没有拐点（点的两端的曲率符号相反）。

光顺的定义：

离散曲线

5. 曲面离散

曲面可以看成若干线性平面的近似，也可以看成平面图的嵌入（参数化）。

半边结构：

Cu为点p的一阶导数的方向，Cuu为点p的二阶导数的方向；设B为Cu和Cuu叉乘的结果的方向，称为从法，N为B和Cu叉乘的结果，称为法向。其中B，N，T构成三维情况下相互垂直的直角坐标系。

曲率：

曲率反映了一点处的弯曲程度，曲率越大，越弯曲，直线任一点处的曲率为0。

切平面：

在点p处，设Su为S(u,v)对u求偏导得到的方向，Sv为S(u,v)对v求偏导得到的方向，设T为Su和Sv的任意的线性组合得到的方向，那么所有的T组成的平面为该点的切平面，且所有的T都是该点的切线。

方向曲率：

在上图中，设黑色加粗曲线为N和T所在的平面与曲面相交的结果 ，这条曲线在点p处的曲率为某个方向的曲率，如果另一平面与曲面相交得到另一条曲线，这条曲线在点p的曲率为另一个方向的曲率，称为方向曲率，曲率是随着方向变化的。

高斯曲率等距变换不变量：由一个面通过变换得到另一个面，面上的每两个点的距离不发生改变，如一张纸弯曲成圆柱的侧面，由于平面上任意一点处的高斯曲率都为0，所以圆柱面和圆锥面上任一点的高斯曲率也都为0。

连续逼近：

 

离散：

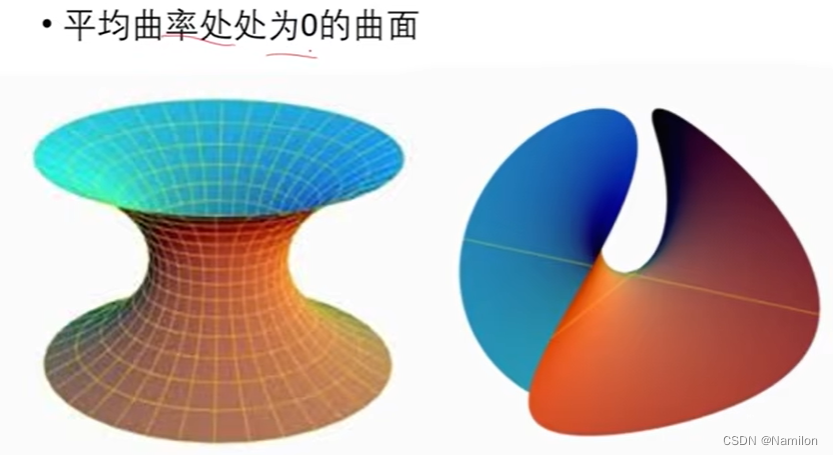
平均曲率：

高斯曲率：

极小曲面：

6. 曲面参数化

    形变

如下图，右下方的点向中心靠拢时，σ1的值逐渐减小；当σ1＜0时，会发生翻转。

参数化方法

Tutte's method

将边界点固定在一个多边形

如果边界为凸多边形，参数化后可以保证所有的三角形网格不会发生翻转，但会造成严重扭曲

Angle Based Flattening（ABF）

以角度作为变量，求解方程组

Foldeover free guaranteed optimization methods

在不发生翻转的前提下，逐渐减少三角形的扭曲程度。 

衡量扭曲程度的方法：

 割缝问题

平面映射

映射的性质

双射：定义域和值域存在一一对应的关系。

对于Flip-free的图形，会出现较明显的扭曲现象。

下图不满足全局双射，但仍满足局部双射。

如果满足全局双射，则处处满足局部双射；如果处处满足局部双射不能得到全局双射的结论。

一个映射的局部是否发生翻转的判断条件为这个映射函数对应的雅克比行列式是否大于0，若大于0则不会发生翻转。

几何优化

无约束优化问题

最优化六：牛顿法（牛顿法、拟牛顿法、阻尼牛顿法）_LittleEmperor的博客-CSDN博客

优化算法——坐标下降法(Coordinate Descent)_坐标下降算法_吃橘子aaaaa的博客-CSDN博客

等式约束

拉格朗日算子法

为了找到fx的极小值点，并且同时满足约束条件，我们希望找到fx的梯度和gx的梯度重合的点。

不等式约束优化

如果给定多个不等式约束，需要在这些不等式组成的可行域空间中寻找fx的极小值。

曲面重建

逆向工程：

可以根据渲染结果求出物体的各个坐标信息，一般只考虑Phong shading的渲染结果。

在多个不同的角度对物体拍照，可以在计算机上重建出该物体。