# 课程介绍
- 计算机图形学大致分成三大块内容:建模(设计,Modeling,内容创建)、动画(仿真,Animation,内容仿真)、渲染(绘制,Rendering,内容呈现),用于构建和创造(虚拟)平行世界;
- 照片(图像):记录真实世界投影在相机成像平面的影像;
- 图像的表达:光栅;(像素固定,放大后会变模糊)
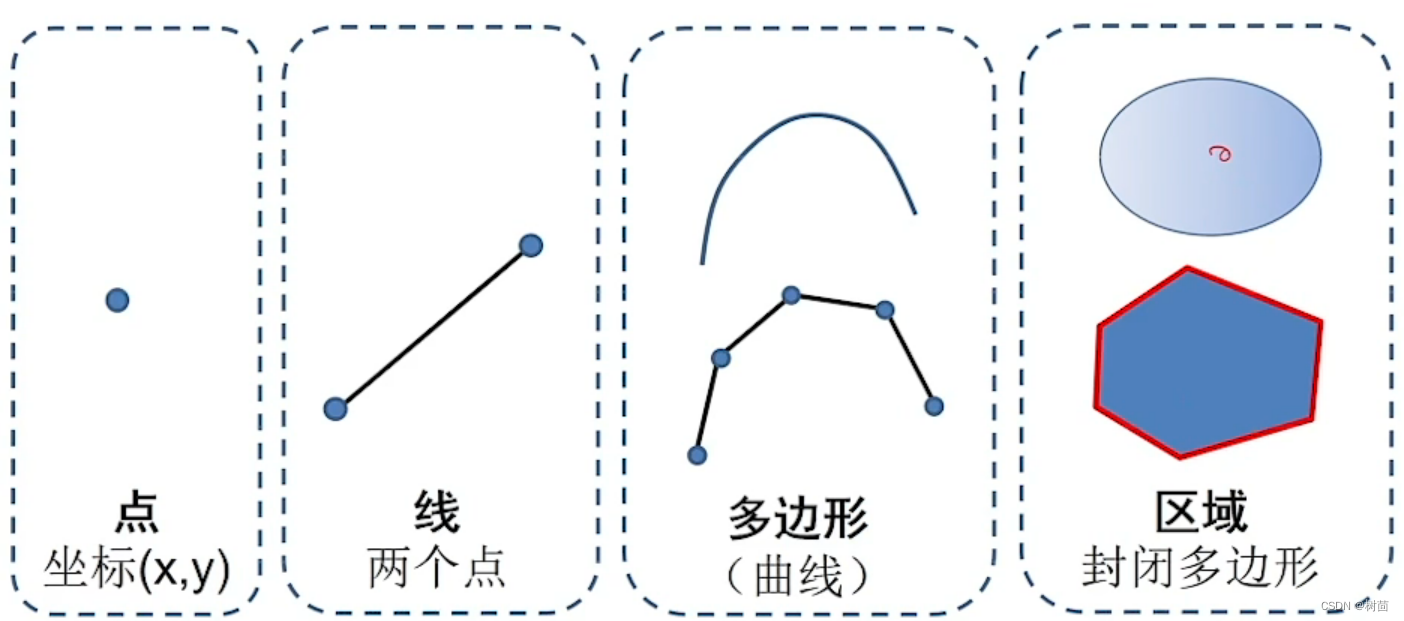
- 2D图形:矢量/几何图形,具有数学表达的几何对象(如:点、线、面)(像素无穷,原本计算机存储的是点线坐标,放大后会根据这些坐标重新光栅化,故不会变模糊)
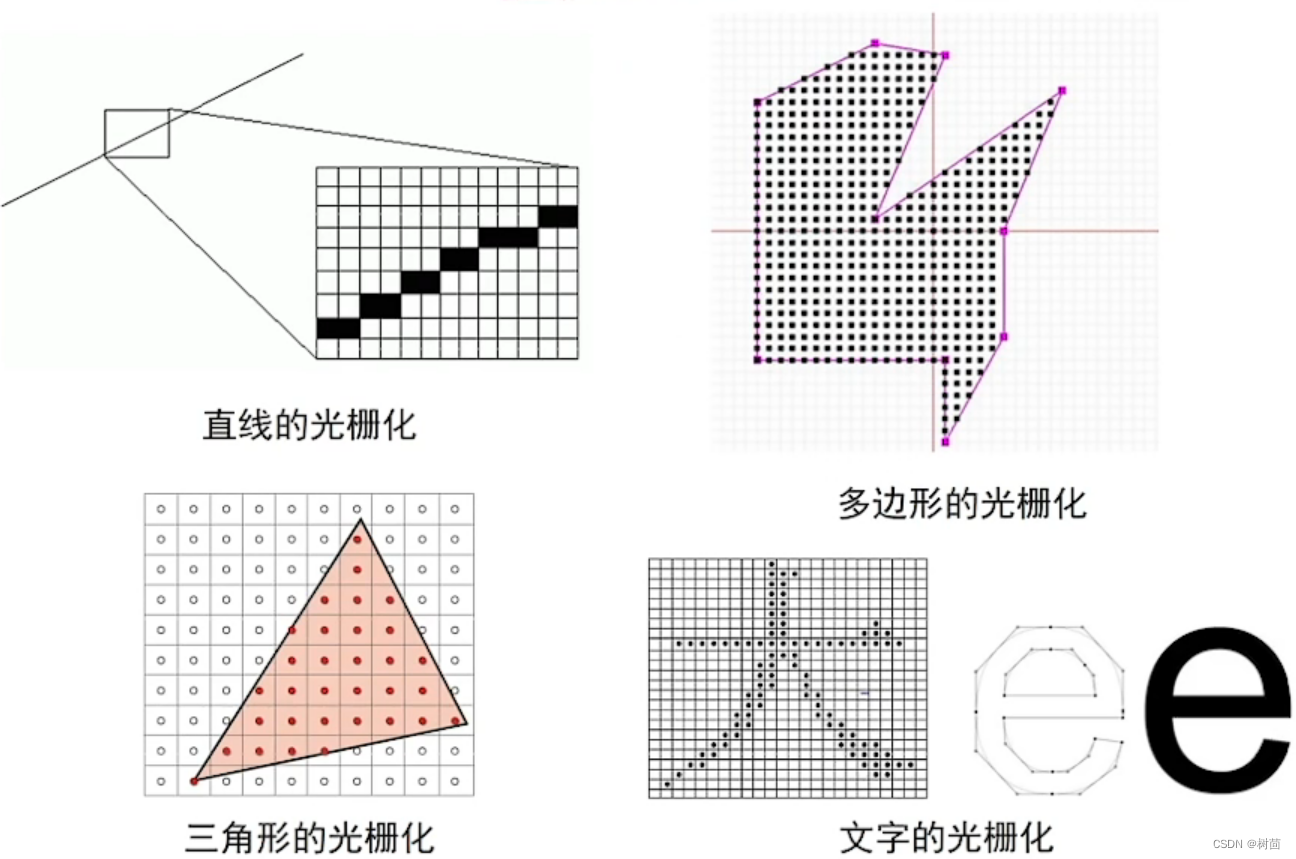
- 图形为了能在计算机屏幕上表达,需要对图形进行光栅化,常用方法有扫描转化;
- 制作三维数据:几何数据、UV展开、贴图(纹理)、材质、灯光、动画...
- 函数拟合:
万能逼近定理(Weierstrass逼近定理):
1、闭区间上的连续函数可用多项式级数一致逼近;
2、闭区间上周期为2pi的连续函数可用三角函数级数一致逼近;

- 大部分的实际应用问题可建模为:找一个映射/变换/函数(输入不一样、变量不一样、维数不一样);
- 如何拟合函数形数据?找函数三步曲:1、哪里找?(确定某个函数集合/空间)2、找哪个?(度量哪个函数是好的/“最好”的,loss)3、怎么找?(求解或优化:不同的优化方法与技巧, 既要快又要好...----最小二乘法)
- 插值:设计的函数一定经过已知的数据点;
- 逼近:函数尽可能靠近数据点,即
;
- 避免过拟合的常用方法:1、数据去噪(剔除训练样本中的噪声);2、数据增广(增加样本数,或增加样本的代表性和多样性);3、模型简化(选用更加简单的模型,或者对模型进行剪裁);4、正则约束(适当的加正则项,如方差正则项、稀疏正则项,使得在第一步哪里找时压力更小,对选择函数的准确性要求更少,使最终使用到的函数集合会自动在训练过程中慢慢优化)
- 岭回归正则项(可使模型更加稳定),用于实现对模型空间的限制,
最小使得W中的每个元素都很小,都接近于0但不为0 ;而参数越小说明模型越简单,越简单的模型则越不容易产生过拟合。

- 稀疏学习:稀疏正则化,用于使得W中的0更多,让参数更加稀疏,从而去除冗余的基函数,通过此操作来选择合适的基函数组成拟合函数。

- 从另一个角度看稀疏约束---压缩感知
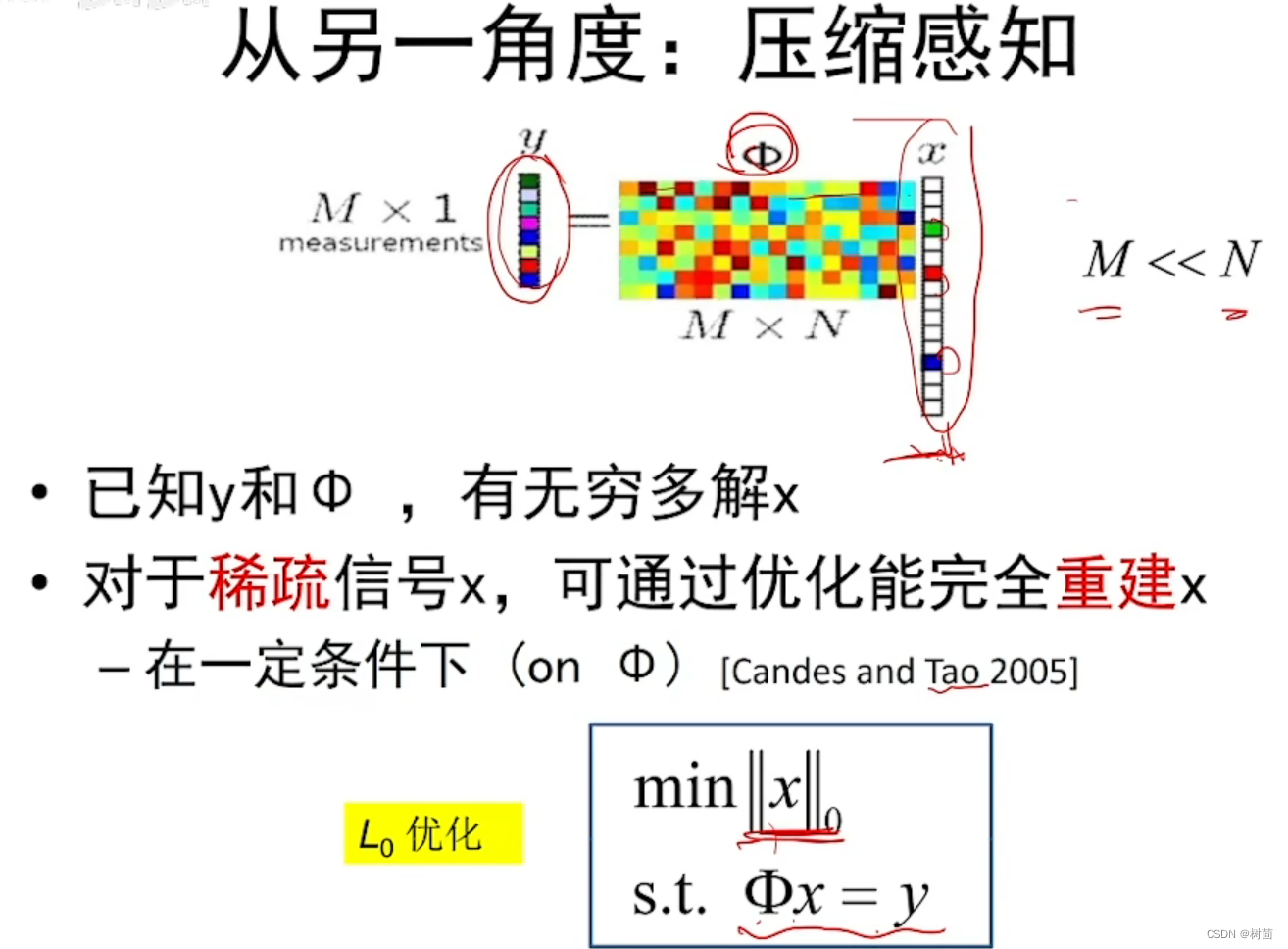
# 数据拟合

- 给系数
的2模加约束防止欠拟合;给系数
的0模加约束去除冗余的基函数稀疏优化;给函数f的两阶导数的平方模加约束约束函数平滑性(因为函数的两阶导数的平方在那个区域的积分度量了函数的光滑性,函数的两阶导数代表曲率);对f函数的弧长进行约束,使其梯度尽量的小;
- 多项式插值存在的问题:1、系统矩阵是稠密的,求解慢;2、依赖于基函数的选取,矩阵可能是病态,导致难以求解(求逆),结果不稳定,控制点的微小变化可导致完全不同的结果;3、振荡(Runge)现象多项式随着插值点数(可以是细微的)增加而摆动;
- 病态问题:输入数据的细微变化导致输出(解)的剧烈变化;
- 用矩阵条件数判断举证病态问题的程度,矩阵条件数=最大1特征值和最小特征值之间的比例,条件数大意味着基元之间有太多的相关性;
- 矩阵奇异值代表矩阵在各个方向的比例;
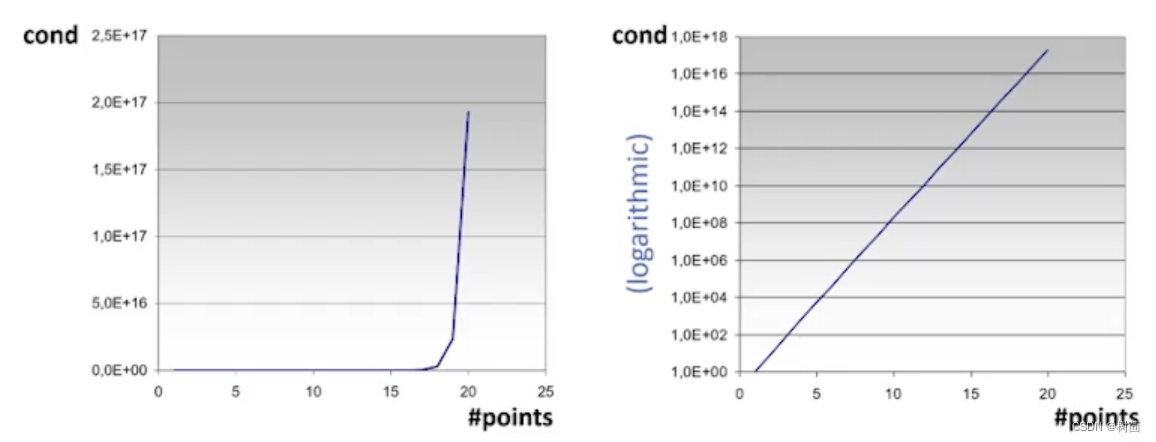
- 多项式插值问题是病态的(过拟合),因为对于等距分布是数据点
,范德蒙矩阵的条件数随着数据点数n呈指数级增长(多项式的最高次数为n-1)
- 好的多项式一般需要系数交替,正负抵消,因此幂函数做基函数就不是一个好的方法,正交函数(即正交多项式)做基函数就是较好的方法;
- 如何获得一般多项式基的正交基?---Gram-Schmidt正交化
- 如何找到更好的基函数来做插值?Bernstein基函数、分片多项式;

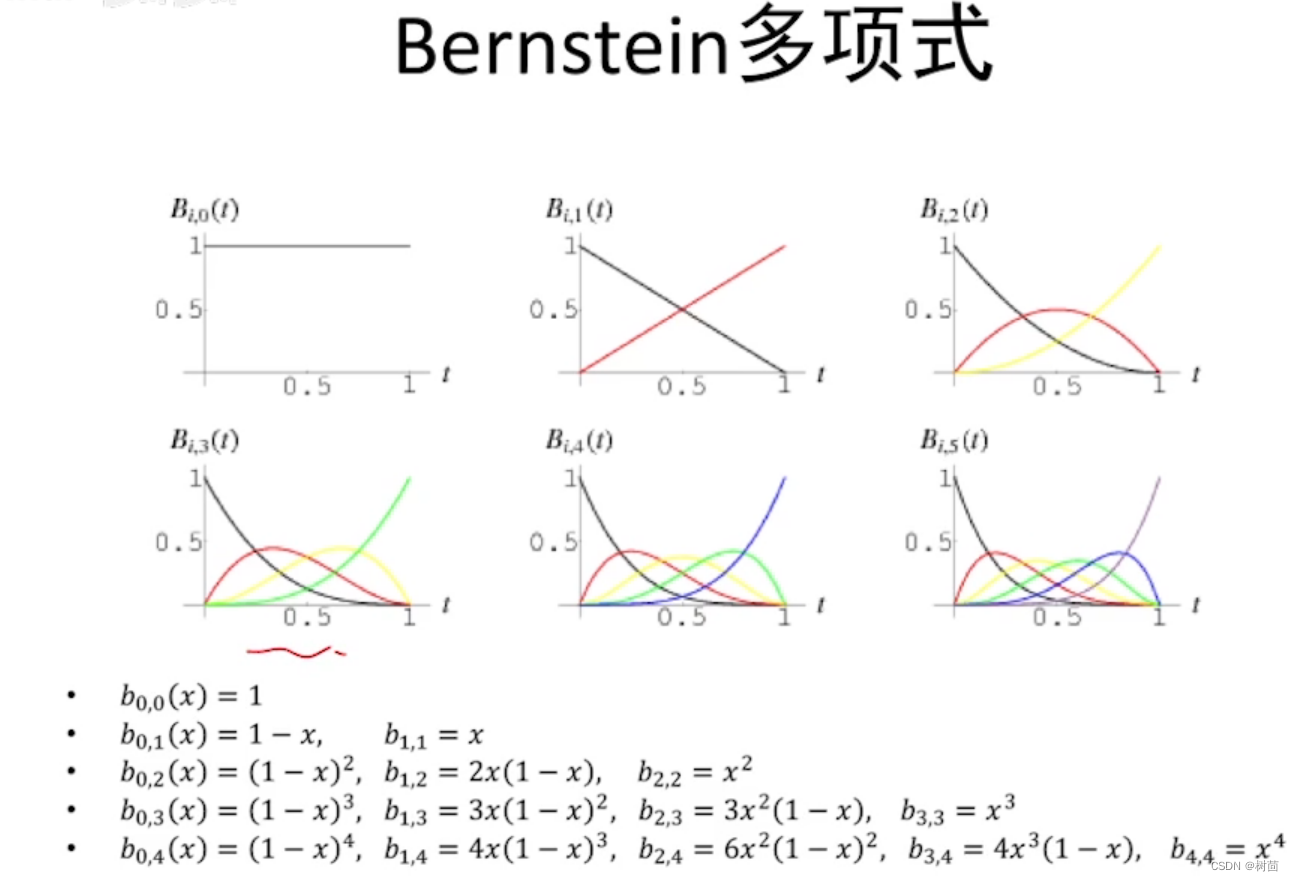
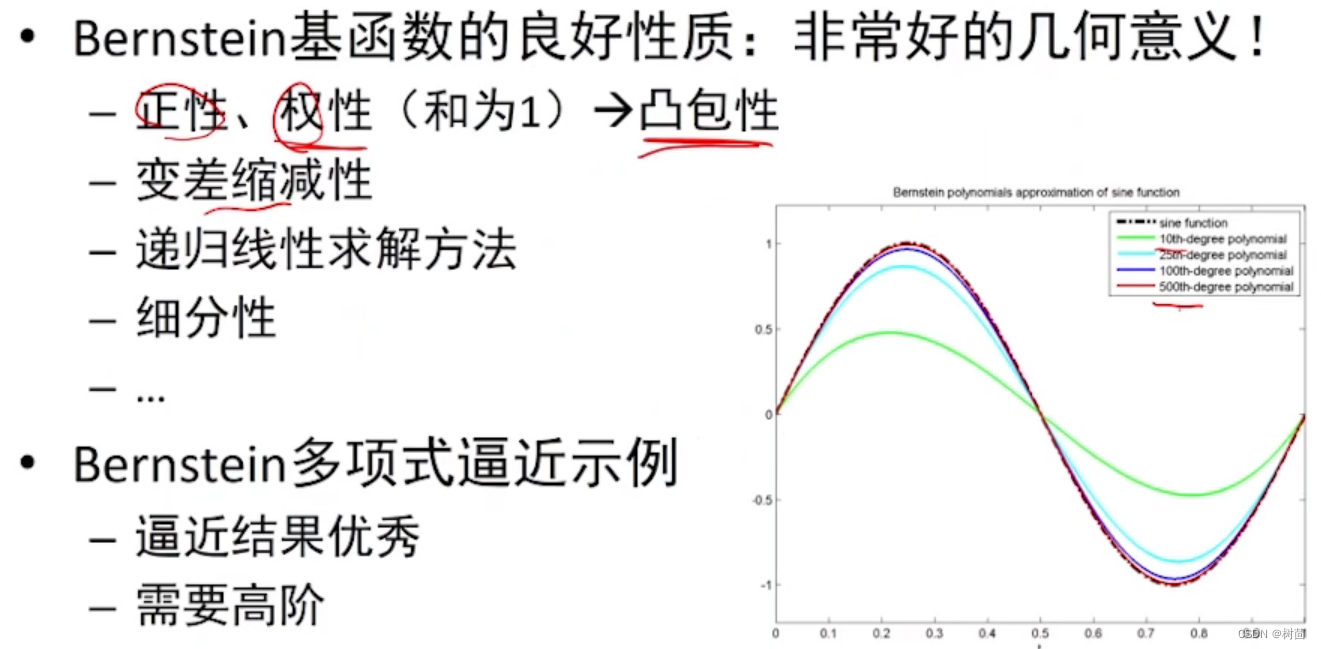
- 为什么选择逼近的方法拟合函数?1、可以降低数据点中噪声、outliers等的影响;2、使函数有更紧凑的表达;3、计算简单、更稳定
- 为什么用多项式?

- RBF函数(在低维中又称Gauss函数)插值/逼近,由于其无论
和
均线性无关,故可以作为基函数;
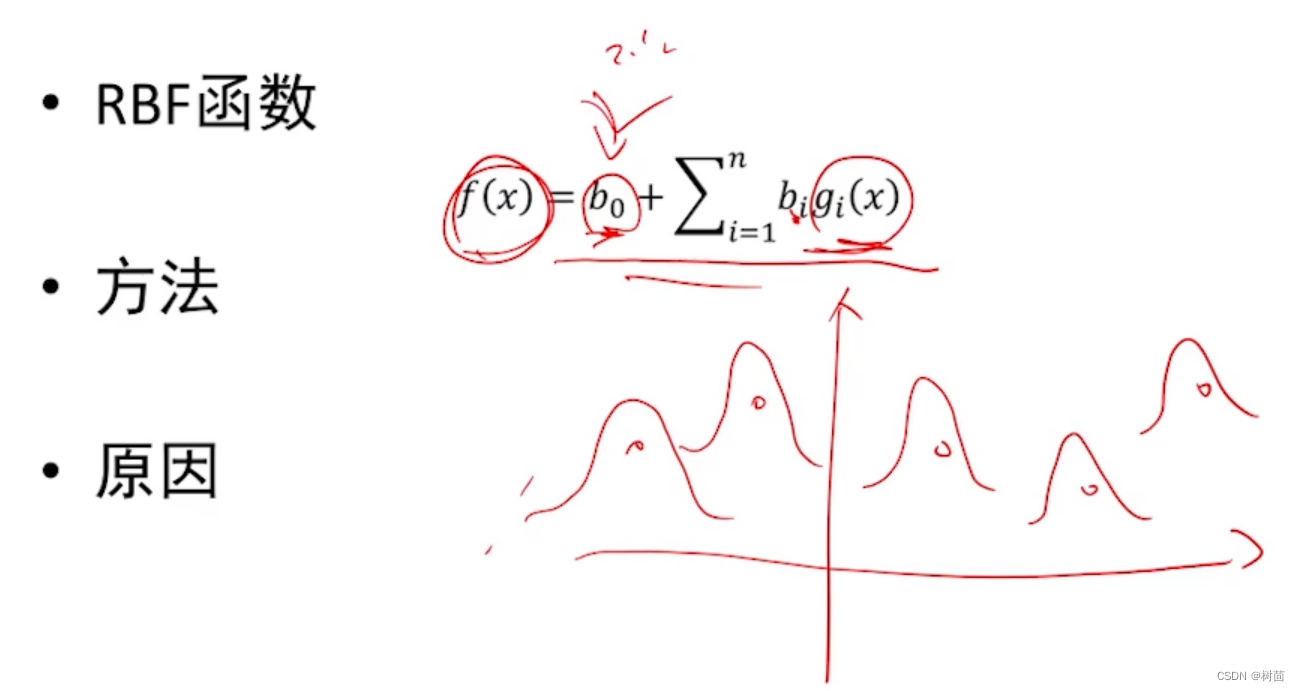
使用RBF函数拟合时不同造成的拟合函数的结果不同,
越小高斯函数越瘦,拟合函数越尖锐:
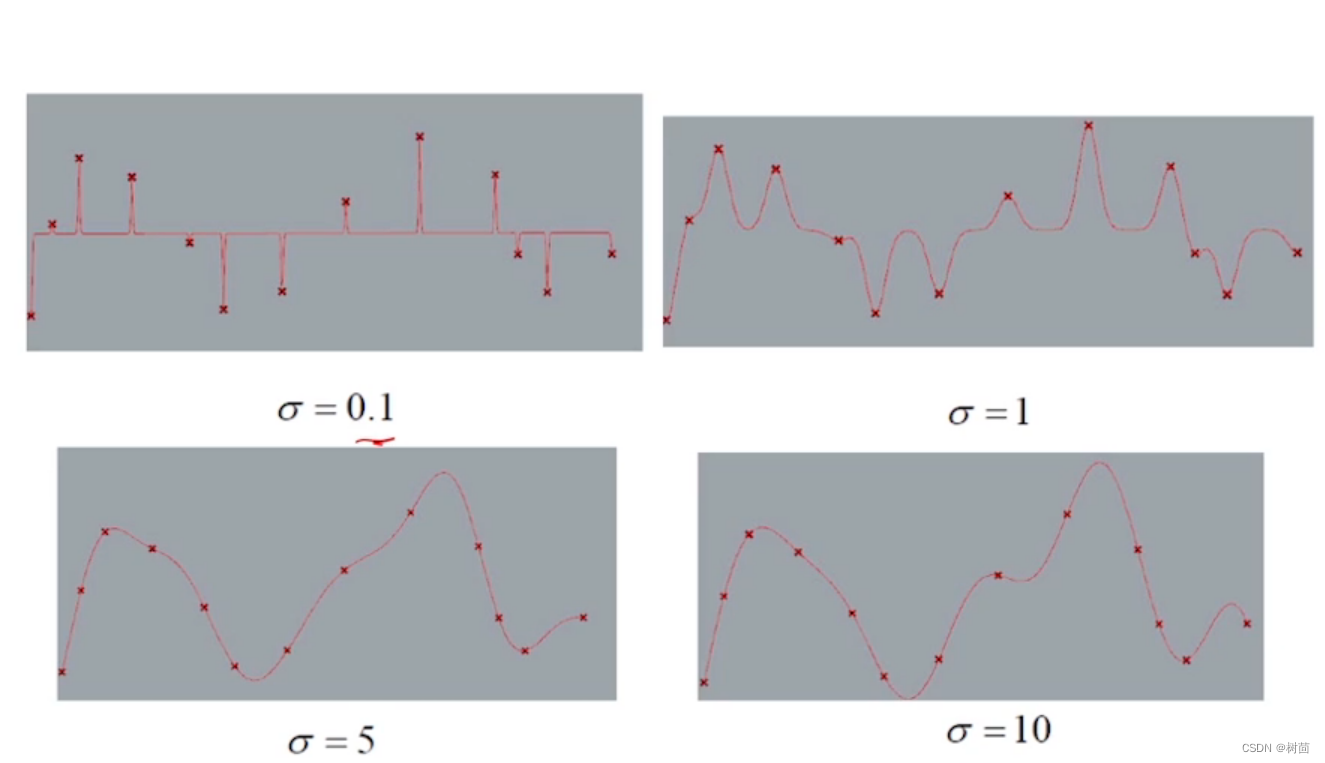
- 如何使得Gauss基函数中的
和
是由要拟合的函数自身定义的而非认为定义?
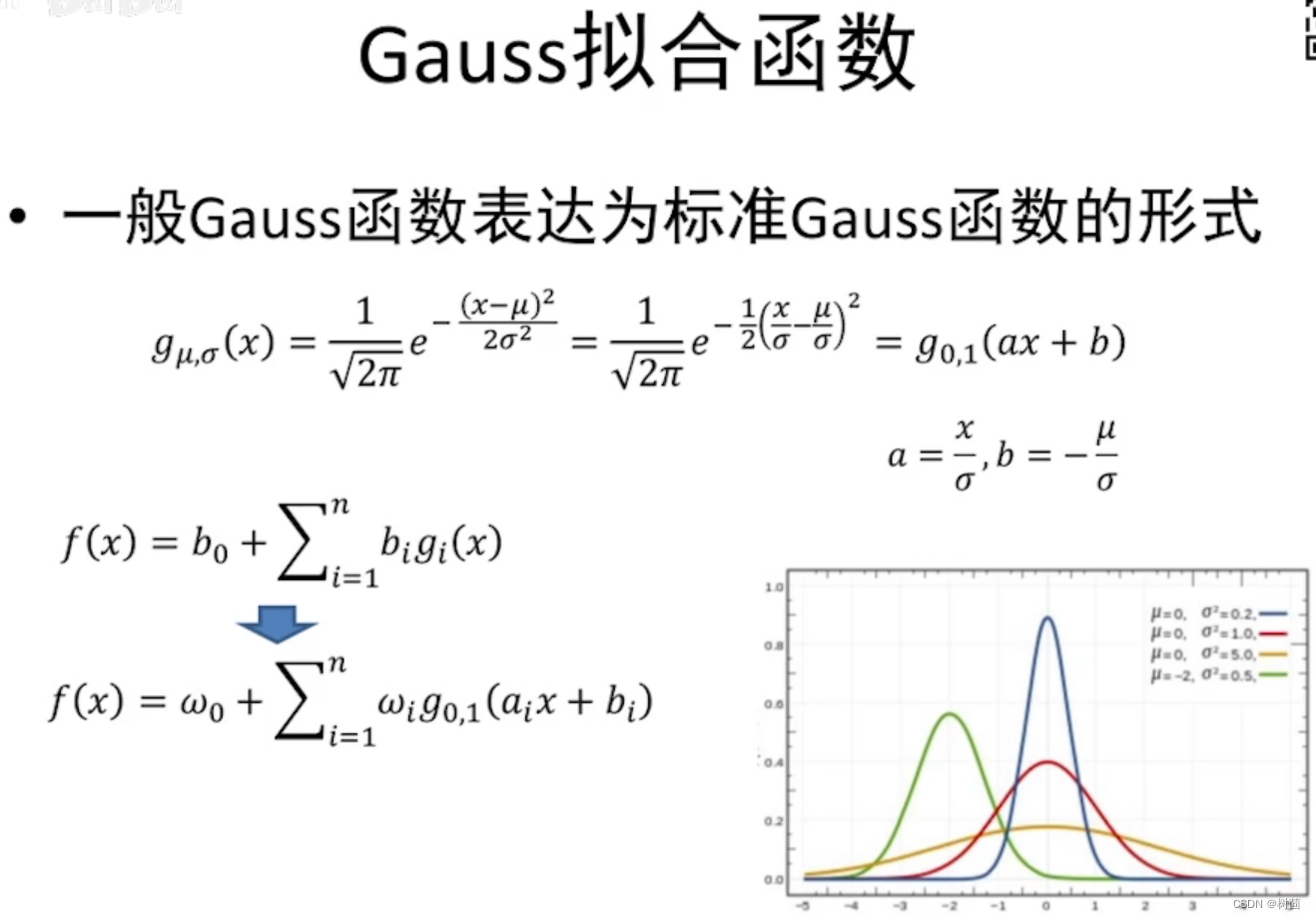
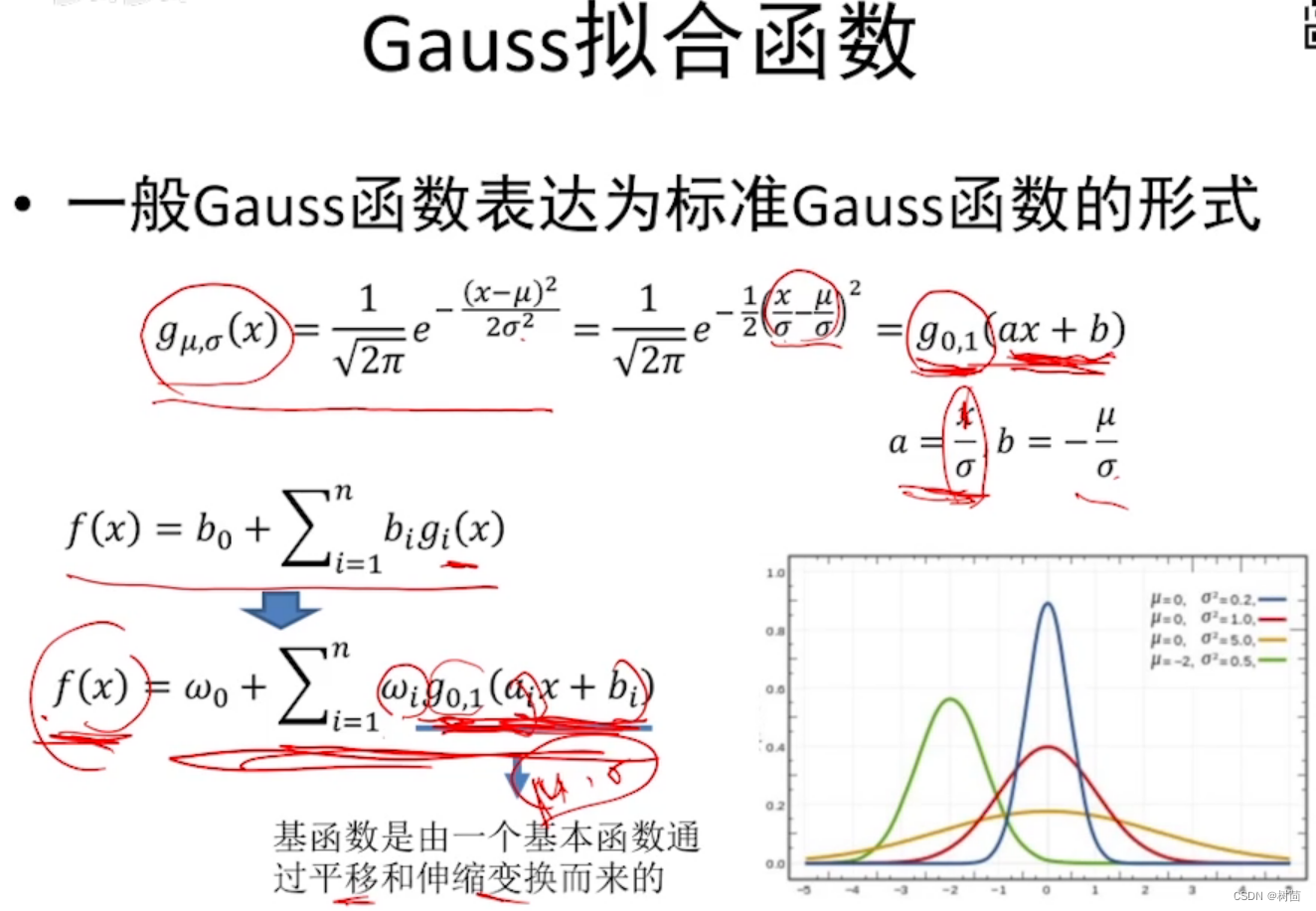
只要和
足够多足够大就可以逼近所有函数;
- 换个方式看上面的函数会发现它就是神经网络!!!
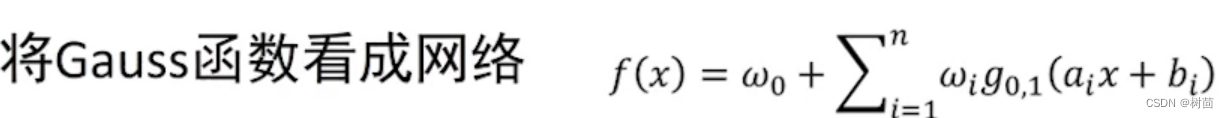
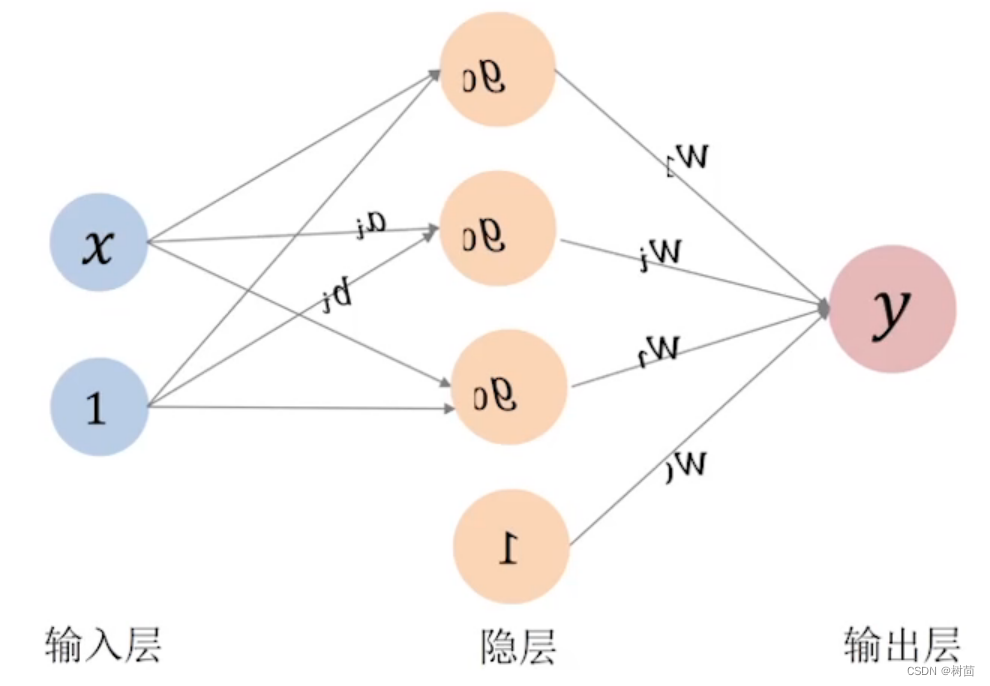
这里的节点个数就是公式中的n,激活函数是
- 高维情形:RBF(Radial Basis Function), 径向基函数,其为一种特殊的BP网络(激活函数为高斯函数),核函数思想,Gauss函数的特性:拟局部性;
- 神经网络本质上是由激活函数张成的函数
- 设定初值是为了让神经网络找到更好的局部最小值
- 激活函数还能如何选择?

- 机器学习的本质:拟合函数
- 高维情形:多元函数

- 万能逼近定理类似:只要单隐层的神经元个数足够多就能逼近任何函数
























 490
490











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








