常用向量相似度衡量指标

1、欧氏距离（Euclidean Distance ）

欧氏距离是最容易直观理解的距离度量方法：

（1）二维平面上点a(x1,y1)与b(x2,y2)间的欧氏距离:

（2）三维空间点a(x1,y1,z1)与b(x2,y2,z2)间的欧氏距离:

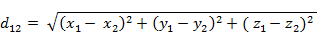
（3）n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的欧氏距离（两个n维向量）：

2、余弦相似度（Cosine similarity）

余弦相似度是通过测量两个向量之间的夹角的余弦值来度量他们之间的一个相似度。0度角的余弦值是1，其他的任何角度的余弦值都不大于1，最小值是-1。

从而两个向量之间角度的余弦值确定了两个向量是否指向同一个方向：两个向量的指向相同时，余弦相似度为1；当两个向量的夹角是90度时，余弦相似度的值为0；两个向量的指向完全相反时，余弦相似度的值为-1。

（这个结果与向量的长度无关，仅仅与向量的指向有关。）

余弦相似度通常用于正空间，因此一般的值为0到1之间。

这个界限对任意维度的向量空间都适用，而且余弦相似度最常应用于高维正空间。

它通常应用于文本挖掘中的文件比较,另外,在数据挖掘领域,常用来度量集群内部的凝聚力.

两个向量之间的余弦值可以通过使用欧几里得点积公式求出:

给定两个属性向量,A和B,其余弦相似性由点积和向量长度给出,如下所示:

3、余弦距离（Cosine distance）

余弦距离就是用1减去余弦相似度获得。

余弦相似度的取值范围是[-1,1]，余弦距离的取值范围是[0,2]。

余弦距离并不是严格意义上的距离，但根据数学上的定义：在一个集合中，如果一对元素可确定一个实数，使得非负性、对称性和三角不等式成立，则该实数可称为这对元素之间的距离。

（1）非负性：余弦距离的取值范围为[0,2]，满足非负性。

（2）对称性：dist(A,B)=1−cosθ=dist(B,A)，满足对称性。

（3）三角不等式：d(x,y) ≤ d(x,z)+d(z,y)，满足三角不等式。

所以，余弦距离可以有效的体现特征向量在方向上的相对差异。（余弦距离使用两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比欧氏距离，余弦距离更加注重两个向量在方向上的差异。）

4、欧氏距离（Euclidean Distance ）与余弦距离（Cosine distance）的异同：

欧氏距离衡量的是空间各点的绝对距离，跟各个点所在的位置坐标直接相关；而余弦距离衡量的是空间向量的夹角，更加体现在方向上的差异，而不是位置。适用于不同的数据分析模型：

（1）欧氏距离能够体现个体数值特征的绝对差异，所以更多的用于需要从维度的数值大小中体现差异的分析；

（2）余弦距离更多的是从方向上区分差异，而对绝对的数值不敏感。

需要注意的是，欧氏距离和余弦相似度都需要保证各维度处于相同的刻度级别，所以一般需要对数据先进行标准化处理，否则很可能会引起偏差。

4、光谱角相似度（SAM）

SAM的概念只存在于多/高光谱图像，普通图像没有这个概念。

SAM又称光谱角相似度，用于度量原始高光谱数据与重构高光谱数据之间的光谱相似度。

把图像中的每个像元的光谱视为一个高维向量，通过计算两向量间的夹角来度量光谱间的相似性，夹角越小，两光谱越相似，属于同类地物的可能性越大，因而可根据光谱角的大小来辨别未知数据的类别。

分类时，通过计算未知数据与已知数据间的光谱角，并把未知数据的类别归为最小光谱角对应的类别中。（计算未知向量与所有已知向量的夹角，将其认为和夹角最小的向量同类别。）

根据两向量间的余弦来计算两向量间（X*未知向量，Xi已知向量）的夹角，即：

 

def sam(x_true, x_pred):
    """
    :param x_true: 高光谱图像：格式：(H, W, C)
    :param x_pred: 高光谱图像：格式：(H, W, C)
    :return: 计算原始高光谱数据与重构高光谱数据的光谱角相似度
    """
    assert x_true.ndim ==3 and x_true.shape == x_pred.shape
    sam_rad = np.zeros(x_pred.shape[0, 1])
    for x in range(x_true.shape[0]):
        for y in range(x_true.shape[1]):
            tmp_pred = x_pred[x, y].ravel()
            tmp_true = x_true[x, y].ravel()
            sam_rad[x, y] = np.arccos(tmp_pred / (norm(tmp_pred) * tmp_true / norm(tmp_true)))
    sam_deg = sam_rad.mean() * 180 / np.pi
    return sam_deg