球形线性插值（SLERP）应用于 LLM 模型融合

最新推荐文章于 2025-12-16 18:22:05 发布

原创最新推荐文章于 2025-12-16 18:22:05 发布 · 454 阅读

CC 4.0 BY-SA版权

文章标签：

《Fine-tuning large language models for domain adaptation: exploration of training strategies, scaling, model merging and synergistic capabilities》

最近看到了关于大模型参数融合的论文，一开始不太明白这类工作的应用意义，看完这篇感觉明白了一些这种方法的价值。这篇论文探索了大型语言模型（LLMs）领域适配的微调策略与模型融合方法，证实球形线性插值（SLERP）融合结合持续预训练（CPT）、监督微调（SFT）、偏好优化（ORPO/DPO）能显著提升专业领域性能，且模型规模（7B/8B 参数）是涌现新能力的关键，1.7B 小模型无此协同效果。

模型融合：将多个经过不同训练路径（如不同微调阶段、不同优化策略）的模型结合，生成一个新模型，其能力超越单个父模型的叠加效果，甚至解锁父模型均不具备的新功能。

中心思想

文章聚焦 LLMs 在材料科学等专业领域的适配难题，通过统一实验框架，系统比较 CPT、SFT、DPO、ORPO 等微调策略及模型融合技术的效果，核心发现：模型融合并非简单参数聚合，而是通过 SLERP 的几何插值实现参数非线性协同，结合多阶段微调能解锁单一模型不具备的新能力；且这种涌现能力依赖模型规模，仅从 7B/8B 级模型中开始显现，为 LLMs 的领域化优化提供了明确路径。

核心贡献中的领域适配方法

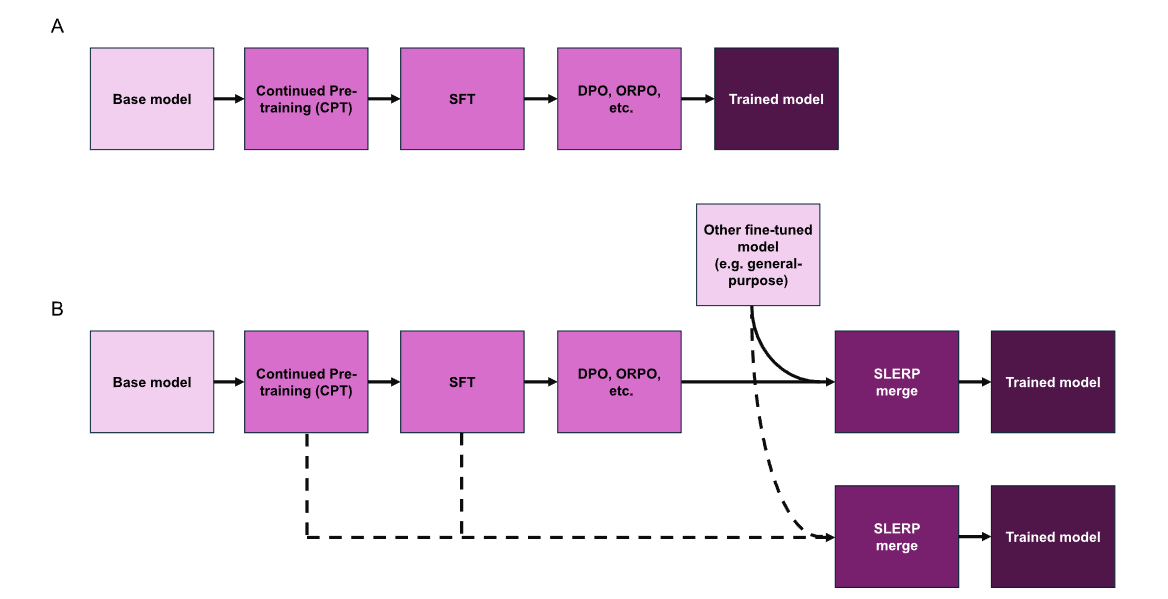
图中A为常规方法，B为本文方法。本文的领域适配通过 “多阶段微调 + SLERP 模型融合” 实现，提出了系统化的 LLM 领域适配框架，既保留通用能力又注入领域专业知识，具体做法如下：

1. 多阶段微调策略

持续预训练（CPT）：用领域原始文本（如材料科学论文）扩展模型知识，不依赖指令模板，仅输入原始文本、推理摘要等，让模型熟悉专业术语和逻辑。
监督微调（SFT）：用标注数据集（问答对、对话数据）训练模型适配特定任务，比如材料设计推理、结构化输出（JSON），提升任务针对性。
偏好优化（DPO/ORPO）：通过 “优选答案 - 劣选答案” 对训练，让模型输出符合领域标准（如科学准确性）和人类偏好，无需复杂奖励模型，效率更高。

2. 模型融合技术

采用球形线性插值（SLERP） 融合不同训练阶段的模型（如领域微调模型 + 通用模型），而非简单参数平均。
核心优势：尊重模型参数空间的几何结构，避免线性插值的高损失区域，触发参数非线性协同，解锁单一模型没有的新能力（如跨材料设计推理）。

3. 配套支撑：数据集与基准构建

构建领域专用数据集：整合蜘蛛丝、生物材料相关论文（共约 5300 + 篇），处理为结构化数据（问答对、JSON 格式研究摘要），保证数据质量（剔除缺陷文本）。
开发专属基准：蜘蛛丝基准（159 题）和生物材料基准（200 题），覆盖知识 recall、逻辑推理、场景应用，全面评估领域适配效果。

模型规模与涌现能力的关系

文本实验明确表明，涌现能力（如超父模型性能、新功能解锁）与模型规模相关，但并非线性递增，核心规律如下：

1. 超阈值模型（7B/8B 参数，Llama 3.1 8B、Mistral 7B）

涌现能力显著：经 “CPT-SFT-ORPO/DPO+SLERP” 适配后，性能远超单一模型平均水平，能完成跨材料推理、生物启发设计等复杂任务。
关键原因：高维参数空间提供足够复杂度，SLERP 融合可激活参数间非线性协同，产生新功能。

2. 亚阈值模型（1.7B 参数，SmolLM）

无涌现能力：即使经过相同微调流程，SLERP 融合后性能未超父模型，甚至略有下降，无法解锁新功能。
但有意外价值：在特定任务（如简单材料设计、图像生成提示构建）中表现亮眼，适合资源受限场景。

3. 核心结论

涌现能力的关键是 “达到参数规模阈值（约 7B 参数）”。
超阈值后，模型架构、微调策略对涌现能力的影响更显著（如 Mistral 7B 经 SLERP 融合后，相对提升超 20%，优于 Llama 3.1 8B）。

SLERP 驱动的模型融合

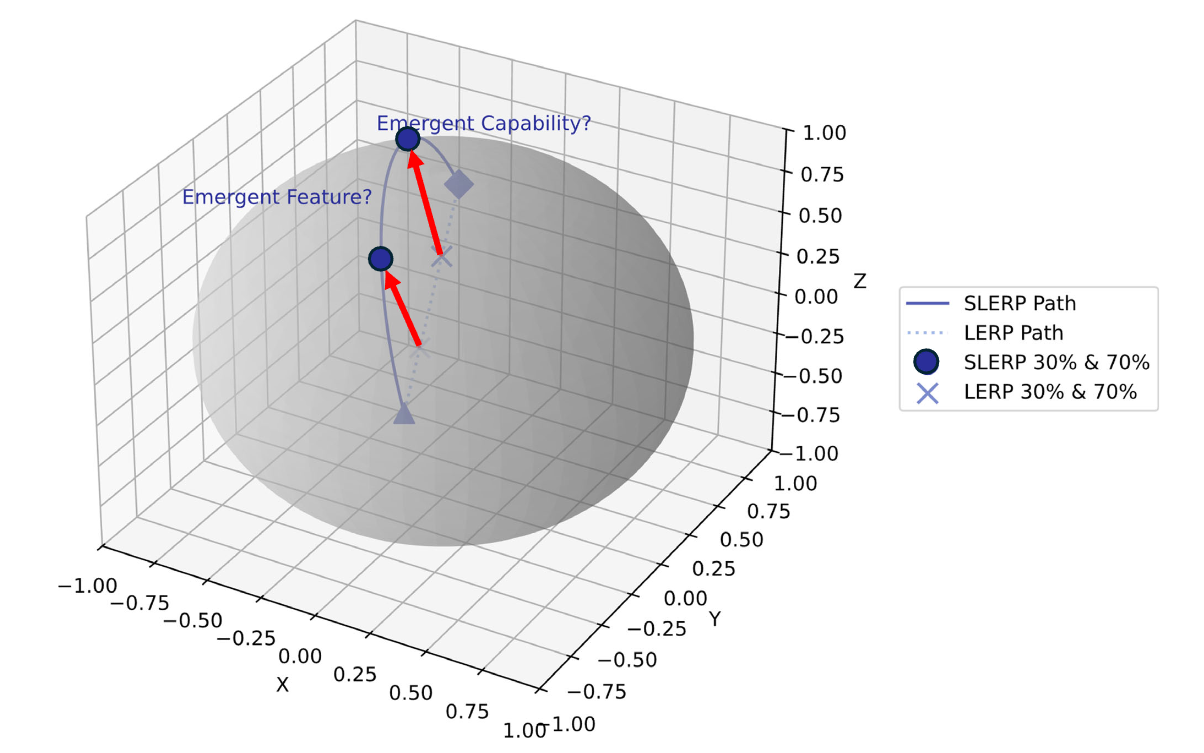
SLERP 比线性插值（LERP）效果好，核心原因是它尊重模型参数空间的几何特性，避免了 LERP 的结构性缺陷。

1. 参数空间本质是 “球面”，而非 “平面”

文章认为，LLM 的高维参数向量更符合 “单位球面” 的几何特性（每个参数向量的模长相对固定，核心差异在方向）。
LERP 假设参数空间是平坦的欧几里得空间，会直接穿过球面进行线性插值 —— 相当于 “破坏” 了参数原有的结构关系，导致插值后的参数失去物理意义（比如模型遗忘原有知识）。
SLERP 则沿球面路径插值，始终保持参数向量的几何关系，不会 “刺穿” 球面，确保参数组合的连贯性和有效性。

3. 保留父模型的核心优势，避免 “破坏性干扰”

LERP 是简单的权重平均，容易让父模型的优势特征相互抵消（比如 A 模型擅长材料知识，B 模型擅长逻辑推理，LERP 可能让两者的优势都被削弱）。
SLERP 通过保持参数向量的角度关系，能 “精准融合” 父模型的互补特征：既保留 A 的专业知识，又保留 B 的推理能力，还能激活两者未单独显现的协同特征（比如用逻辑推理整合专业知识，生成更严谨的科学结论）。

4. 触发非线性协同，解锁涌现能力

LERP 的线性组合只能产生 “父模型能力的平均”，无法产生新功能；而 SLERP 的球面插值是一种非线性操作，能让参数间产生复杂交互。
文章通过数学推导证明：SLERP 的插值公式（含正弦函数调节）能让参数组合产生 “新的特征激活”（比如原本 A 模型的参数 θ₁和 B 模型的 θ₂，融合后会激活新的特征 φᵢ），这正是涌现能力的来源。

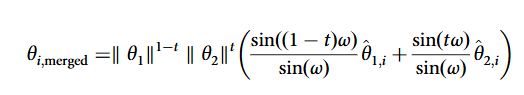
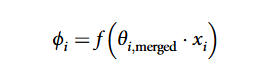
看完这篇文章后，有一些疑问：

一、为什么要假设参数空间是球形？

高维参数的 “方向主导” 特性：LLM 的参数是高维向量（如 7B 模型有数十亿个参数，对应数十亿维向量），训练过程中参数更新主要调整向量 “方向”，而 “模长”（向量长度）相对稳定（不会出现某一维度参数值急剧增大或减小的情况）。这种 “模长近似固定、方向决定功能” 的特点，与 “单位球面” 上的点（半径固定、方向各异）高度契合。
适配 SLERP 的原生优势：SLERP 原本用于计算机图形学的 “旋转插值”（旋转本质是球面运动），其核心价值是保持插值过程的 “几何一致性”。将 LLM 参数空间建模为球形，能直接复用这一特性，让模型融合时参数交互更平滑，避免高损失区域。

二、如何证明这种球形建模的合理性？

文章采用结果导向，通过实验验证建模的有效性—— 即基于球形假设的 SLERP 融合，能产生可复现的性能提升，间接证明该假设符合 LLM 参数的实际特性：

性能远超平面假设的 LERP：实验显示，SLERP 融合模型的性能显著高于 LERP，而 LERP 融合仅能达到父模型性能的平均水平，甚至下降。这种差距证明，球形假设更能捕捉参数的真实交互规律。
涌现能力的一致性：所有 7B/8B 级模型（Llama、Mistral）在 SLERP 融合后，均涌现出父模型不具备的新能力（如跨材料设计推理、结构化 JSON 输出），且效果稳定可复现。若球形假设与参数空间特性不符，这种涌现能力应是随机或不存在的。
小模型的反证：1.7B 参数的 SmolLM 因参数维度低、空间复杂度不足，无法形成 “方向主导、模长稳定” 的特性，此时 SLERP 融合不仅无增益，反而性能下降。这反过来说明，当参数空间具备 “球形适配特性”（高维、方向主导）时，建模才有效，进一步验证了假设的针对性。

补充：高维空间的统计学依据

高维向量的统计学特性：在高维空间中，随机向量的模长会趋于稳定（“高维球面集中现象”），且任意两个随机向量的夹角近似垂直。LLM 的参数经大量训练后，本质是高维空间中 “非随机的有效向量”，其模长稳定性和方向特异性，恰好符合球形建模的前提 —— 这为假设提供了统计学层面的合理性支撑。