A Self-Attentive model for Knowledge Tracing

A Self-Attentive model for Knowledge Tracing

1 Introduction

关于学生知识概念（KC）的大量学生学习轨迹数据集的可用性，其中KC可以是练习、技能或概念，吸引了数据挖掘人员开发用于预测学生表现和提供适当反馈的工具[8]。知识追踪（knowledge tracing，KT）被认为是开发个性化学习平台的一项重要任务，被定义为根据学生过去的学习活动，追踪学生的知识状态，它代表了学生对KCs的掌握程度。KT任务可以形式化为有监督的序列学习任务-给定学生过去的练习交互X=（x1；x2；：：；xt），预测他/她的下一次交互的某些方面xt+1。在问答平台上，交互表示为xt=（et；rt），其中et是学生在时间戳t尝试的练习，rt是学生答案的正确性。KT旨在预测学生是否能正确回答下一个练习，即预测p（rt+1=1jet+1；十）。

最近的深度学习模型，如deep Knowledge Tracing（DKT）[6]及其变体[10]，使用递归神经网络（RNN）在一个汇总的隐向量中对学生的知识状态进行建模。动态键值记忆网络（DKVMN）[11]为KT开发了记忆增强神经网络[7]。利用键和值两个矩阵，分别学习习题与基础KC和学生知识状态之间的相关性。DKT模型面临着参数不可解释的问题[4]。DKVMN比DKT更具解释性，因为它显式地维护一个KC表示矩阵（key）和一个知识状态表示矩阵（value）。然而，由于这些深度学习模型都是基于RNN的，因此在处理稀疏数据时面临着不能泛化的问题。

在本文中，我们建议使用一种纯粹的基于注意力机制的方法，即转化器[9]。在KT任务中，学生在经历一连串的学习活动时建立的技能是相互关联的，对某一特定练习的表现取决于他在与该练习相关的过去练习中的表现。例如，在图1中，一个学生要解决属于知识概念 "方程 "的 “二次方程”（练习5）的练习，他需要知道如何找到 “平方根”（练习3）和 “线性方程”（练习4）。本文提出的SAKT首先从过去的互动中识别相关的KC，然后根据学生在这些KC上的表现来预测他/她的成绩。为了预测学生在练习中的表现，我们把练习作为KC。正如我们在后面所展示的，SAKT在预测学生在某一特定练习上的表现时，对先前回答的练习分配了权重。所提出的SAKT方法明显地超过了最先进的KT方法，在AUC上获得了4:43%的性能改进，在所有数据集上平均如此。此外，SAKT的主要组成部分（自我注意）适合于并行，因此，我们的模型比基于RNN的模型快了一个数量级。

2 Proposed Method

我们的模型根据学生之前的互动序列$X=x_1,x_2,...x_t$预测他是否能够回答下一个练习$e_{t+1}$。 如图2所示，我们可以将该问题转化为一个顺序建模问题。考虑模型的输入$x_1,x_2,...x_{t-1}$和提前一个位置的练习序列$e_2,e_3,...e_t$是很方便的，输出是对练习$r_2,r_3,...,r_t$的反应的正确性。互动元组$x_t=(e_t,r_t)$以数字$y_t=e_t+r_{t}E$的形式呈现给模型，其中$E$是练习的总数量。 因此，互动序列中的一个元素可以采取的总数值是$2E$，而练习序列中的元素可以采取$E$的可能数值。
我们现在描述一下我们架构的不同层次。

• Embedding layer：我们将得到的输入序列$y=(y_1,y_2,...,y_t)$转换为$s=(s_1,s_2,...,s_n)$，其中n是模型能够处理的最大长度。由于该模型可以处理固定长度序列的输入，如果序列长度$t$小于$n$，我们会重复地在序列的左边添加一个问题-答案对的填充。然而，如果$t$大于$n$，我们将序列划分为长度为$n$的子序列。具体来说，当$t$大于$n$时，$y_t$被划分为$t/n$个子序列，每个子序列的长度为$n$。所有这些子序列作为模型的输入。
  我们训练一个交互嵌入矩阵，$M\in R^{2E\times d}$，其中$d$是潜在的维度。这个矩阵被用来为序列中的每个元素$s_i$获得一个嵌入，$M_{s_i}$。同样地，我们训练练习嵌入矩阵，$E\in R^{E\times d}$，使集合$e_i$中的每个练习都被嵌入到第$e_i$行。
  Position Encoding：位置编码是自我注意神经网络中的一层，用于编码位置，这样就像卷积网络和循环神经网络一样，我们可以对序列的顺序进行编码。这一层在知识追踪问题中尤为重要，因为学生的知识状态会随着时间的推移而逐渐稳定地演变。在一个特定的时间实例中，知识状态不应该出现波浪式的转换[10]。为了纳入这一点，我们使用了一个参数，即位置嵌入，$P\in R^{n\times d}$，它是在训练时学习的。然后，位置嵌入矩阵的第i行被添加到交互序列的第i元素的交互嵌入向量中。
  嵌入层的输出是嵌入式交互输入矩阵$\hat{M}$和嵌入式练习矩阵$\hat{E}$。
  
• Self-attention layer：在我们的模型中，我们使用了缩放点积注意力[9]。这一层找到了对应于以前解决的每一个练习的相对权重，以预测当前练习的正确性。我们使用以下公式获得query和key-value对。
  
  其中$W_Q,W_K,W_V\in R^{d\times d}$分别是查询、键和值的投影矩阵，它们将各自的向量线性地投影到不同的空间[9]。以前的每个互动与当前的练习的相关性是通过注意力权重来确定的。为了找到注意力权重，我们使用缩放点积[9]，表示为:
  
  Mutiple heads：
  为了共同关注来自不同代表子空间的信息，我们使用不同的投影矩阵对查询、键和值进行线性投影h次。
  
  其中headi = Attention(^ EWQ i ; ^MWKi ; ^MWVi )，WO 2 Rhdd。
  Causality：
  在我们的模型中，在预测(t+1)次练习的结果时，我们应该只考虑前t次的相互作用。因此，对于一个查询Qi，不应该考虑j>i的键Kj。我们使用因果关系层来掩盖从未来的交互键中学习的权重。
• Feed Forward layer：上面描述的自我注意层的结果是以前的互动的值Vi的加权和。然而，从multihead layer得到的矩阵的行，$S=Multihead(\hat{M},\hat{E})$仍然是以前互动的值，$V_i$的线性组合。为了在模型中加入非线性，并考虑不同潜伏维度之间的相互作用，我们使用一个前馈网络。
  
  其中$W^{(1)}\in R^{d\times d},W^{(2)}\in R^{d\times d},b^{(1)}\in R^d,b^{(2)}\in R^d$是在训练中学习的参数。
• Residual Connections：残差连接[2]用于将低层的特征传播到高层。因此，如果低层特征对预测很重要，残差连接将有助于将它们传播到进行预测的底层。在KT的背景下，学生尝试属于一个特定概念的练习来加强该概念。因此，残差连接可以帮助传播最近解决的练习的嵌入，使模型更容易利用低层的信息。剩余连接被应用在自我注意和前馈层之后。
• Layer normalization：在[1]中，有研究表明，将不同特征的输入归一化可以帮助稳定和加速神经网络。为了同样的目的，我们在我们的架构中使用了层归一化。层归一化也被应用在自注意层和前馈层。
• Prediction layer：最后，上面得到的矩阵Fi的每一行都通过具有Sigmoid激活的全连接网络来预测学生的成绩。
  pi = Sigmoid(Fiw + b); (6) 其中pi是一个标量，代表学生对练习ei做出正确反应的概率，Fi是F的第i行，Sigmoid(z) = 1=(1 + ez)
• Network Training：训练的目的是使模型下观察到的学生反应序列的负对数可能性最小。通过最小化pt和rt之间的交叉熵损失来学习参数。
  

Notations	Description
N	学生总人数
E	练习的总数量
X	一个学生的互动序列。(x1, x2, …, xt)
$X_i$	一个学生的第$i$个练习-答案对
n	序列的最大长度
d	潜在向量的维度
e	学生解决的练习序列
M	交互嵌入矩阵
P	位置嵌入矩阵
E	习题查询矩阵
$\hat{M}$	过去的互动嵌入
$\hat{E}$	练习嵌入

3 Experimental Settings

3.1 Datasets

为了评估我们的模型，我们使用了四个真实世界的数据集和一个合成数据集。

• 合成数据集1：这个数据集是通过模拟4000个虚拟学生的答题轨迹得到的。每个学生回答相同的50道练习，这些练习来自5个不同难度的虚拟概念。
• ASSISTment 2009（ASSIST2009）。这个数据集是由ASSISTment在线辅导平台提供的，被广泛用于KT任务。我们在更新的 "技能建设者 "数据集上进行了实验。该数据集是稀疏的，因为该数据集的密度为0:06，如表2所示。
• ASSISTment 2015（ASSIST2015）：ASSISTment2015包含学生对100种技能的回答。有19,917名学生和708,631次互动。虽然这个数据集的记录数比ASSISTment 2009多，但由于学生人数更多，每个学生的平均记录数更少。这个数据集是所有可用数据集中最稀疏的，其密度为0:05。
• ASSISTment Challenge（ASSISTChall）。这个数据是从ASSISTment 2017比赛中获得的4。就互动数量而言，它是最丰富的数据集，有942,816次互动，686名学生和102项技能。这个数据集是所有可用数据集中最密集的数据集，因为其密度为0:81。
• STATICS2011（STATICS）。这个数据集包含一个工程静力学课程的交互，有189,927个交互，333个学生和1223个技能标签。我们采用了[11]中的处理数据。它也是一个密集的数据集，密度为0.31。
  所有数据集的完整统计信息可以在表2中找到。
  
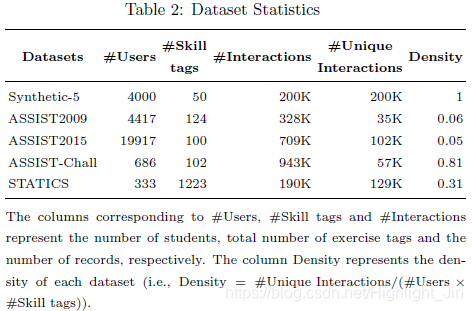
  与#Users、#Skill tags和#Interactions对应的列分别表示学生人数、练习标签总数和记录数量。密度栏表示每个数据集的密度。

3.2 Evaluation Methodology

Metrics：预测任务是在二分类的环境下考虑的，即回答一个练习正确与否。
因此，我们使用曲线下面积（AUC）指标来比较性能。

Approaches：我们将我们的模型与最先进的KT方法、DKT[6]、DKT+[10]和DKVMN[11]进行比较。这些方法在介绍中有所描述。

Model Training and parameter selection：我们用80%的数据集训练模型，并在剩余的数据集上测试。对于所有的方法，我们尝试了隐藏状态维度d={50,100,150,200}。对于相互竞争的方法，我们使用了与它们各自论文中报告的相同的超参数。对于权重的初始化和优化，我们使用了与[10]类似的程序。我们用Tensorflow实现了SAKT，并使用ADAM[5]优化器，学习率为0.001。我们对ASSISTChall数据集使用了256个批次的大小，对其他数据集使用了128个批次的大小。对于记录数量较多的数据集，例如ASSISTChall和ASSIST2015，我们使用0.2的放弃率，而对于其余的数据集，我们使用0:2的放弃率。我们将序列的最大长度n设定为与每个学生的平均练习标签大致成正比。对于ASSISTChall和STATICS数据集，我们使用n=500，对于ASSIST2009 n=100和50 ，对于合成和ASSIST2015数据集n被设置为50。

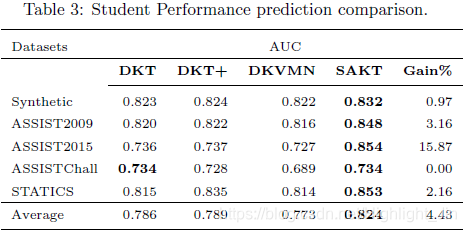
1 粗体数字为最佳性能。
2 报告的结果是由每个数据集的最佳超参数选择单独得到的。

4 Results and Discussion

Student Performance Prediction：表3显示了SAKT与当前最先进方法的表现比较。在合成数据集上，SAKT的表现优于其他方法，其AUC为0.832，而DKT+的AUC为0.824。尽管合成数据集是最密集的数据集，但SAKT的性能优于基于RNN的方法，因为它采用了生成合成数据集的方法。对于这个数据集，每个单独的练习只来自一个概念。使用项目反应理论确定学生正确回答来自该数据集的练习的概率$p(correct|\alpha ,\beta )=c+\frac{1-c}{1+exp(\beta -\alpha )}$; 其中c表示正确猜测的概率，$\alpha$和$\beta$ 是随机选择的数字，分别表示概念能力和练习难度。因此，在这个数据集中，属于同一概念的练习具有很强的相关性。与其他基准不同，SAKT直接尝试识别属于同一概念的练习，因此比其他方法表现更好。在ASSIST2009上，SAKT的性能优于其他方法，比第二好的方法提高了3.16%。对于ASSIST2015数据集，SAKT显示出令人印象深刻的15.87%的改善。我们将这一优势归因于这样一个事实，即SAKT利用的注意机制即使在数据集稀疏的情况下也能很好地学习和推广，ASSIST2015就是这种情况，因为它的密度在其他数据集中是最小的。对于STATICS2011，我们的方法比DKT+的性能提高了2.16%。对于ASSISTChall，我们的方法的性能与DKT相当。这可以归因于这样一个事实，即ASSISTChall是所有真实世界数据集中最密集的数据集。

Attention weights visualization：将过去交互的元素（作为关键）和学生接下来要解决的练习（作为查询）之间的注意力权重可视化，可以帮助理解过去交互中的哪些练习与查询练习相关。在这个动机下，我们计算了所有序列中每个练习对（e1,e2）的注意权重之和，其中e1作为查询，与练习e2的交互作为关键。然后，我们将注意力权重归一，使每个查询的权重之和为1。这就产生了一个相关性矩阵，其中每个元素（e1,e2）代表e2对e1的影响。我们在Synthetic上进行分析，因为这个数据集是用已知的隐藏概念生成的，因此关于不同练习的相关性的基本事实对我们来说是已知的。图3a显示了对应于Synthetic中练习的相关性矩阵的热图。对于Synthetic来说，所有的序列由同一序列中的所有练习标签组成，从1到50开始。
为了建立练习标签之间的影响图，如图3b所示，我们使用相关性矩阵。首先，我们抽出序列中属于每个隐藏概念的第一个练习，并访问相关性矩阵的每一行，将该行对应的练习与基于边缘权重排名的前两个练习连接起来，边缘权重与这对练习之间的注意力权重成正比。我们可以看到，基于注意力权重，我们能够实现基于隐藏概念的练习标签的完美聚类。一个有趣的观察是，两个在序列中相距甚远但属于同一概念的练习可以被SAKT识别出来。例如，如图3b所示，一个关于练习22的查询将最多的权重分配给练习5的关键，即使它们在序列中出现的时间相差甚远。
两个相互关联的练习往往有很高的关注权重，因为其中一个练习的表现会影响另一个练习的表现。此外，在现实世界中，在序列中出现的练习很接近，往往属于同一个概念。因此，我们预计注意力的权重会偏向于在交互序列中最近出现的练习。为了说明这一点，我们手动分析了ASSIST2009数据集，以可视化一些选定样本的注意力权重。表4显示了一些练习以及过去的交互和分配给每个交互的注意力权重。

Ablation Study：表4显示了默认SAKT架构和所有变体在所有数据集上的性能（d=200）。

• No Positional Encoding。在默认架构的这个变体中，我们删除了位置编码。因此，为预测学生在特定练习中的表现而分配的注意力权重只取决于交互嵌入，而不受其在序列中的位置影响。在ASSIST2009和ASSIST2015中，数据集是稀疏的，因此去除PE的影响不像ASSISTChall和STATICS这样密集的数据集那样明显。
• No Residual Connection (RC)：RCs显示了低层次特征的重要性，即在进行预测时的交互嵌入。由于我们的结构不是很深，所以RC对模型的性能贡献不大。事实上，对于ASSIST2015数据集来说，去除残余连接后的性能比默认值更好。
• No Dropout：Dropout在神经网络中被用来规范化模型，使其能够更好地泛化。与模型的参数数量相比，对记录数量较少的数据集来说，模型的过度处理更为有效。因此，Dropout对ASSIST2009数据集和STATICS数据集的作用更为有效。
• Single head：我们没有像默认结构那样使用5个头，而是尝试只使用一个头的变体。多头有助于捕捉不同子空间中的注意力权重。在所有的数据集上，使用单头会使SAKT的性能持续下降。
• No block：当不使用自我注意块时，对下一次练习的预测只取决于最后一次互动。可以看出，没有注意力块，性能明显比默认架构差。
• 2 Blocks：增加自我注意块的数量会增加模型的参数数量。然而，在我们的案例中，参数的增加并没有被证明对提高性能是有用的。原因是预测学生在某项练习中的表现的一个重要方面是取决于他在过去相关练习中的表现。增加另一个自我注意的模块使模型更加复杂。

Training efficiency：图4展示了在训练阶段基于GPU上运行时间的各种方法的效率。计算效率比较，SAKT在一个epoch中只花费1.4秒，比DKT+（65秒/epoch）少46.42秒，是DKT（45秒/epoch）的32倍，是DKVMN（26秒/epoch）的17.33倍。我们在nvidiatitanv型GPU上进行了实验。

与Exercise tag相对应的列指查询（即，我们必须预测学生表现的练习）和与过去的交互相对应的列指为该学生观察到的交互序列。
右列中的红色元素表示过去交互元素中最重要的元素。

（a） 热图描绘了每对练习之间的注意力权重。注意，分配给对（i,j） ，其中j>i总是零，因为所有序列都是以相同的顺序从1-50。

（b） 描述练习之间相关性的图表。相关性是由在使用SAKT的练习中学习到的注意权重决定的。我们观察到潜在概念的完美聚类。
图3：可视化合成数据集的注意力权重。

5 Conclusion and Future Work

本文提出了一个基于自我注意的知识追踪模型SAKT。它模拟了一个学生的交互历史（不使用任何RNN），并通过考虑他过去交互中的相关练习来预测他在下一个练习中的表现。在各种真实数据集上的大量实验表明，我们的模型比最新的方法具有更好的性能，并且比基于RNN的方法快一个数量级。