转载地址:http://blog.csdn.net/sunshine_in_moon/article/details/45749691
本文转自知乎大牛。
从定义出发,Ax=cx:A为矩阵,c为特征值,x为特征向量。
矩阵A乘以x表示,对向量x进行一次转换(旋转或拉伸)(是一种线性转换),而该转换的效果为常数c乘以向量x(即只进行拉伸)。
我们通常求特征值和特征向量即为求出该矩阵能使哪些向量(当然是特征向量)只发生拉伸,使其发生拉伸的程度如何(特征值大小)。这样做的意义在于,看清一个矩阵在那些方面能产生最大的效果(power),并根据所产生的每个特征向量(一般研究特征值最大的那几个)进行分类讨论与研究。
更新与2015.12.02 今天无意中看到了这篇介绍,感觉讲的很清晰,特与大家分享!
连接:http://jingyan.baidu.com/article/3065b3b68c6bb6becff8a488.html
大学中都学过矩阵,是不是矩阵感觉很抽象,晦涩难懂,和生活实际挂不上边,其中矩阵有一个叫特征向量的东西,只要学过矩阵的,都会求它,但是他是做什么的,书本上却没说,只是说相当有用,但是在何处用,大家只能说 I do not know ,这里给大家说明下,特征向量的几何意义,让大家一目了然
工具/原料
纸
笔
记得带着脑子哦
方法/步骤
如果说一个向量v是方阵A的特征向量,将一定可以表示成下面的形式:
这时候λ就被称为特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式:
其中Q是这个矩阵A的特征向量组成的矩阵,Σ是一个对角阵,每一个对角线上的元素就是一个特征值。首先,要明确的是,一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵:
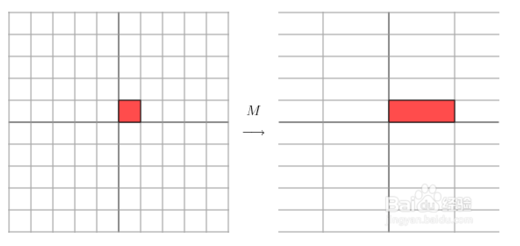
它其实对应的线性变换是下面的形式:
因为这个矩阵M乘以一个向量(x,y)的结果是:
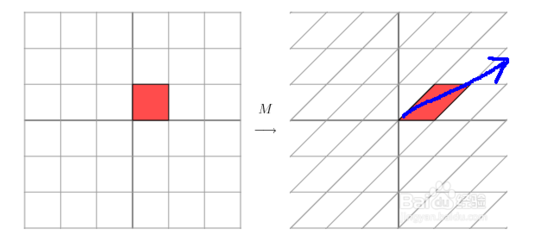
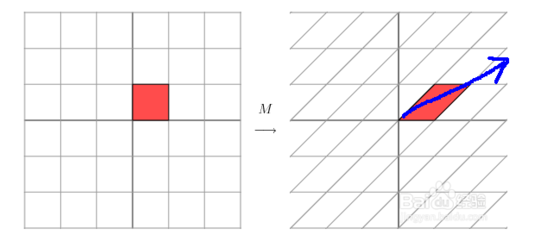
上面的矩阵是对称的,所以这个变换是一个对x,y轴的方向一个拉伸变换(每一个对角线上的元素将会对一个维度进行拉伸变换,当值>1时,是拉长,当值<1时时缩短),当矩阵不是对称的时候,假如说矩阵是下面的样子:
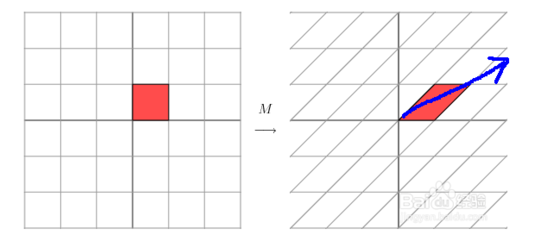
它所描述的变换是下面的样子:
这其实是在平面上对一个轴进行的拉伸变换(如蓝色的箭头所示),在图中,蓝色的箭头是一个最主要的变化方向(变化方向可能有不止一个),如果我们想要描述好一个变换,那我们就描述好这个变换主要的变化方向就好了。反过头来看看之前特征值分解的式子,分解得到的Σ矩阵是一个对角阵,里面的特征值是由大到小排列的,这些特征值所对应的特征向量就是描述这个矩阵变化方向(从主要的变化到次要的变化排列)
当矩阵是高维的情况下,那么这个矩阵就是高维空间下的一个线性变换,这个线性变化可能没法通过图片来表示,但是可以想象,这个变换也同样有很多的变换方向,我们通过特征值分解得到的前N个特征向量,那么就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向,就可以近似这个矩阵(变换)。也就是之前说的:提取这个矩阵最重要的特征。总结一下,特征值分解可以得到特征值与特征向量,特征值表示的是这个特征到底有多重要,而特征向量表示这个特征是什么,可以将每一个特征向量理解为一个线性的子空间,我们可以利用这些线性的子空间干很多的事情。不过,特征值分解也有很多的局限,比如说变换的矩阵必须是方阵。
注意事项
最后一个条是关键,一定要仔细看
在此基础上理解PCA就方便了许多。








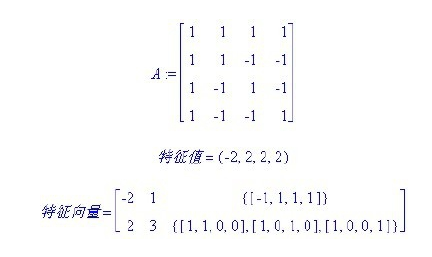
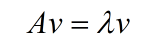
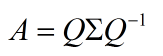
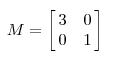
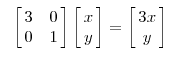
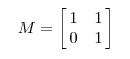
















 1983
1983

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








