球面面积的积分推导

已于 2024-12-11 10:50:24 修改
阅读量1k 收藏
点赞数 1
文章标签： 笔记 数学建模 几何学
于 2024-12-11 10:47:33 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/LLdalin/article/details/144393446
版权

最近鬼事神差的去重温大学物理，导致必须先去捡微积分的知识，想起求球表面积的积分推导，在B站上也看到求表面积的视频，他们都是先求球体体积，再求表面积，我觉得有点绕远求近了，所以我自己写了一点直接球表面积积分的推导，聊以记录。

下面这个图我花了好久时间画的。

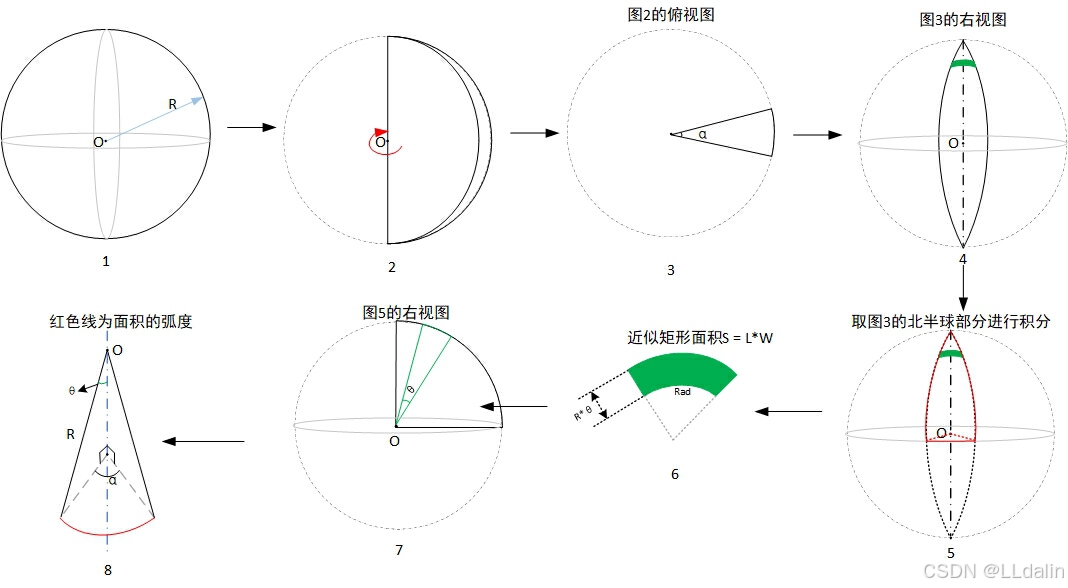
接下来说一下我的微分思路：

半圆沿球体轴线绕行一周形成球体。取半圆绕行α角度形成的形状S进行研究，取S表面角度为θ的绿色部分进行研究。

         当α和θ在微分领域后，变成dα和dθ，微分面积dS = Rad*\theta *R d\theta。

         Rad的求取如最后一张图所示，R在α角平面的投影长度为R*sinθ，而轴线上α角平面的扇形区域对应的弧度Rad =d\alpha *R*sin\theta，由于Rad最大处对应的是赤道上的弧度，南北半对称，取北半进行积分。

对θ积分有：S = 2*\int_{0}^{\pi/2}d\alpha *R*sin\theta *R*\theta d\theta =2d\alpha R^{2}*\int_{0}^{\pi/2}sin\theta *\theta d\theta 

积分结果是 S =2*R^{2}d\alpha

对α积分有：S = \int_{0}^{2\pi }2*R^{2}d\alpha = 2R^{2} \int_{0}^{2\pi }d\alpha ,积分结果是 S = 4\pi R^{2}。

至此推导结束。

望诸君共勉！

LLdalin
关注
数学分析(二十一)-重积分6-重积分的应用1：曲面的面积
u013250861的博客
02-02 792
§ 6 重积分的应用 重积分的应用除前面提到的可用以求空间立体的体积及空间物体的质量外,这里再举几个它在几何与力学方面的应用. 一、曲面的面积 设 DDD 为可求面积的平面有界区域, 函数 f(x,y)f(x, y)f(x,y) 在 DDD 上具有连续的一阶偏导数, 讨论由方程 z=f(x,y),(x,y)∈Dz=f(x, y),(x, y) \in Dz=f(x,y),(x,y)∈D 所确定的曲面 SSS 的面积. 为了定义曲面 SSS 的面积, 对区域 DDD 作分割 TTT, 它把 DDD分成 nnn
圆柱、圆锥的侧面积和球的表面积公式推导（不用积分）
weixin_33744854的博客
12-25 2292
其实这里有个问题，就是表面积本来就是用积分定义的。标题上说「不用积分」，只是说不是计算积分，而是按照定义导出未知面积和已知面积的关系，从而导出所需公式。 圆柱的侧面积 对于圆柱，经常看到的推法是把侧面展开成平面图形（长方形）。这虽然很直观，但到底什么叫「展开」，根本说不清楚。 用表面积的定义，可以严格化这个所谓的「展开法」。 微积分对表面积的定义是「曲面切平面上的长方形面积微元和的极限」。...
【数学】立体角，积分求球的表面积、体积
一切皆可视
05-15 3万+
对于做实时光线跟踪的理论学习来说，立体角是个非常基础又重要的概念，因此我们要对其进行惮述。在平面圆中我们定义了角的一个衡量标准：弧度。也即当圆的半径时，该圆心角的弧长的值即为弧度。 针对三维中球面的概念，我们定义了立体角。先看图： 假若球的半径为，那么我们定义如图所示的锥形，也即：由水平角和垂直角的变化量和交叉形成的一小块区域，现在来估算它的面积 近似的我们认为它是个长方形，其中由决定的...
球的表面积公式是怎么推导出来的？
知道这个有什么用？
11-27 3万+
球的体积公式的推导 球的表面积公式是： 证明方式一：体积求导 基本思路： 可以把半径为R的球，从球心到球表面分成n层，每层厚为 r/n ，像洋葱一样。半径获得增量是△r，体积增加的部分的体积就为△V。  极限的思想：当△r趋近于零时，球的每层的厚度就薄的像个曲面一样，这部分很薄的体积，除以dr就是球的表面积了。 继续追问：为什么x3求导是3x2？ 证明方式二：将球拆成无数个小的四棱锥 如下图： 基本思想： 把整个球体分切成无数的锥体，每一个锥体的底面都是球体表面的一小部分。对球体不断进行分切，
【数学】使用积分推导圆的面积公式
一切皆可视
05-14 1万+
本文将使用积分公式简明扼要的证明圆的面积公式 第一步：划分求微元 将圆心角在划分为n份，对应圆周上的点为 其中最大的一份圆心角为，因为圆心角的弧度值就是其对应的边长的弧长/r，因此就代表其圆心角最大。 任取一个划分求其对应的微元的面积，拿弧长近似为底，r为高，也即图中海绿色的部分 注意这里使用了圆心角的弧度值就是其对应的边长的弧长/r。 第二步：求和求极限 求和 ，注意求和是约...
【Ray Tracing The Rest of Your Life】第2章 使用蒙特卡洛计算一重积分与球面积分
一切皆可视
05-30 1910
这一章代码简单，但是理解起来颇有难度，又很重要，望仔细阅读。 代码使用VS2015编写。 链接：https://pan.baidu.com/s/1hmTUkAiXFd8Q0Lqy4Zt8bg 提取码：jgg8 第一步：理解pdf 积分经常被用来计算面积或者体积，在图形学中应用颇广。之前我们渲染的图形都有噪点（比如【Ray-Tracing In Next Week】第6章 矩形和灯光...
数学物理方程—积分复习
Leslie Lee's blog includes programming in math, physics, and engineering.
08-24 5435
三维直角坐标系 dxdydz 柱坐标系 drdθdz 球坐标系 drdθdφ 令x=rcosθ y=rsinθ dxdydz = 令x=rsinφcosθ y=rsinφsinθ z=rcosφ dxdydz =
2021-04-09
kuangben2000的博客
04-09 5144
bing UnitVectorToOctahedron 图形学几何数学知识 https://www.jianshu.com/p/59b71d2bfdf4 图形学几何数学知识 残编断简 2020.08.06 15:26:00字数 1,174阅读 71 1. 球面积分 球面积分跟普通的线性积分的区别在于需要考虑到半径的长度，因此只需要利用极坐标公式将球面积分转换为线性积分即可。 坐标系示意图 用球面坐标系表示，某个点的坐标为，各个变量含义如上图所示，变量的范围给出如下： ...
空间面积解算
Jin Shuting
11-09 6454
空间面积的解算 通常情况下，在地球表面的一个小范围区域，投影变形较小，我们用平面面积代替球面面积，两点间的弧长等效为两点间的距离，两条相交的曲线间的夹角等效为两线段间的夹角。经证明：当边长小于200km时，椭球面上三角形的解算完全可以在平面上进行。此时，椭球面三角形与球面三角形各对应角的差异小于0.001秒，边长差异则小于1mm。 但如果是地理跨度比较大的区域，投影变形较大，用平面面积代替曲面面...
常用函数连续傅里叶变换对照表
04-15
将常用的连续函数的傅里叶变换及其对偶性质整理成文档，便于查阅
圆面、球面上的采样方法
syddf
10-23 6297
（本文内容主要来自《pbrt》13.5、13.6） 如果yyy满足概率密度分布p(y)p(y)p(y)，如果要随机地获取一个yyy的话，可以先获取一个随机数ttt，然后代入它的累积概率密度P(y)=tP(y)=tP(y)=t，然后求解出yyy即可。 但是很多情况需要的不仅是对单个变量做采样，往往需要对多个维度下的多个变量进行采样，而这些多个变量之间很有可能有互相关联，并且直接采样也不容易，可以考虑...
球面坐标系下的三重积分
qq_39377889的博客
02-09 1万+
（防止忘了记在这里）微积分的进阶应用之球面积分的计算，这种积分是在球面坐标系进行的，适用于积分区域为球或球的部分、锥或锥的部分。
数学有关的知识点
nhl19961226的博客
04-16 5804
【球冠的面积】 链接：传送门 假定球冠最大开口部分圆的半径为 r ，对应球半径 R 有关系：r = Rc osθ，则有球冠积分表达： 球冠面积微分元 dS = 2πr*Rdθ = 2πR^2*cosθ dθ 积分下限为θ，上限π/2 所以：S = 2πR*R(1 - sinθ) 其中：R(1 - sinθ)即为球冠的自身高度H 所以：S = 2πRH S=∫dS =∫2πr*...
为什么球的表面积不能用周长积分而体积可以用面积积分？
黄佳俊的博客
12-13 2964
数学，积分，表面积
球体积公式推导（积分）
热门推荐
nan
11-19 5万+
球的体积 刚刚学了定积分的一点皮毛…来玩一玩 废话不多说，Let’s start 设球的半径为RRR 我们把球（我们通过半球来考虑）切成好多好多（nnn片）薄片，就是一个一个的圆，设圆的半径分别为rrr 面积 S(r)=πr2S(r)=\pi r^2S(r)=πr2 到圆心距离为xxx的圆的半径 f(x)=R2−x2f(x)=\sqrt{R^2-x^2}f(x)=R2−x2​ 可以得到 V=2∫0...
圆面积公式积分法推导
TMS_LI的专栏
11-23 2万+
圆的面积推导背景这个方法是本人独立发现的，维基上了有相同的证明，称为洋葱证法(Onion proof)。 通过个方法，能帮助理清类似的积分应该情形。圆的面积公式：S=πr2 S = \pi r^2 推导考虑从圆心以某一半径向外生长的方式，某一个半径r处，如果半径增量很少，面积增量可以看成2πrdr2\pi r dr, 即此处的柱面面积,生长速度即导数为2πr2\pi r关键点：增加面积为什么是可看
微积分（一）一般概念以及从圆的面积怎么来？
learn process of Hanna
03-20 1万+
今天开始回忆或者说重学一下微积分，在此记录一下课程总结以及拓展。我们都知道圆的面积是，但是，为什么呢？我们来看一下这个公式的由来。仔细观察我们就能发现了解的微积分中的几个idea：积分，导数。假设想要计算一个半径为3的圆的面积，首先将整个圆分成几个同心圆。我们以内部的一个半径为r（0<r<3）的圆环为例，试图找出这个圆环的面积。那么将这个圆环变形展开，能得到一个近似的长方形，它的长度为...
球面坐标积分
最新发布
03-22
在球面坐标系下的积分是一种常见的数学计算方法，尤其适用于涉及三维空间的问题。以下是关于如何在球面坐标系下进行积分的一些关键点和具体方法： --- ### 方法一：理解球面坐标的定义 球面坐标由三个参数组成：径向距离 $r$、极角 $\theta$ 和方位角 $\phi$。 它们与直角坐标的关系如下： $$x = r \sin\theta \cos\phi$$ $$y = r \sin\theta \sin\phi$$ $$z = r \cos\theta$$ 体积元素在球面坐标系中表示为： $$dV = r^2 \sin\theta \, dr \, d\theta \, d\phi$$ 这表明，在球面坐标系下进行三重积分时需要考虑这个额外的因子。 --- ### 方法二：设定积分范围 对于一个完整的球体，通常取值范围为： - 径向距离 $r$: 从0到球半径R； - 极角 $\theta$: 从0到$\pi$； - 方位角 $\phi$: 从0到$2\pi$。 例如，若要计算单位球内的体积，则可以设置以下积分： $$\int_0^{2\pi} \int_0^\pi \int_0^1 r^2 \sin\theta \, dr \, d\theta \, d\phi$$ --- ### 方法三：实际应用中的例子 以求解函数$f(r,\theta,\phi)$在一个球形区域上的积分为例，其形式化表达为： $$I = \iiint_V f(r,\theta,\phi) \cdot r^2 \sin\theta \, dr \, d\theta \, d\phi$$ #### 示例代码实现 (Python) ```python import numpy as np from scipy.integrate import tplquad def integrand(phi, theta, r): # 定义被积函数f(r, θ, φ)，这里我们选择简单的常数函数1为例 return r**2 * np.sin(theta) # 设定积分限 result, error = tplquad(integrand, 0, 1, lambda r: 0, lambda r: np.pi, lambda r, theta: 0, lambda r, theta: 2*np.pi) print(f"Integral result: {result}, Error estimate: {error}") ``` 此段代码实现了对单位球内体积的积分计算。 --- ### 注意事项 确保正确转换边界条件至球面坐标系统；检查是否所有角度都覆盖完整周期（即避免遗漏某些特定方向）。同时也要留意不同物理场景可能带来的特殊约束或者简化情况。 ---
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值