动量法(Momentum)

动量法通过在梯度下降更新中引入动量，使参数更新不仅依赖于当前的梯度，还考虑了之前的更新方向。

原理

动量法的主要思想是通过引入动量项来加速梯度下降算法的收敛速度，并减少更新过程中的震荡。具体来说，动量法引入了一个动量项，该动量项记录了之前几步的梯度更新情况，并根据这些信息调整当前的参数更新方向和幅度。

核心公式

动量法引入动量项 vt 表示参数更新的方向和幅度：

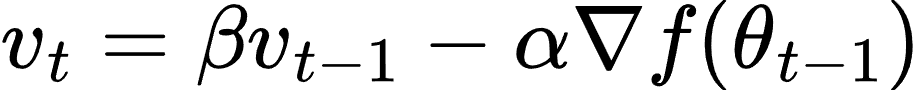
然后更新参数：

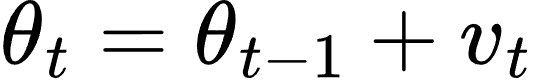
其中：

• vt为第 t 次迭代的动量
• β 为动量系数，一般取值在 0.9 到 0.99 之间
• α 为学习率
• ∇f(θt−1) 为当前梯度

直观解释

可以把动量法想象成一个小球在凹凸不平的地面上滚动。梯度下降算法就像是小球在每一步只受当前坡度（梯度）影响。而动量法则像是小球带有一定的惯性，不仅受当前坡度影响，还会受之前滚动方向和速度的影响。这样，当小球遇到坑洼时不会来回震荡太多，而是会更平滑地滚动下去。

代码案例

动量法通过在梯度下降中加入动量项来加速收敛。下面是一个使用动量法优化一个复杂函数的示例，并包含多个数据分析图形。

import numpy as np
import matplotlib.pyplot as plt

# 定义一个复杂函数及其梯度
def func(x):
    return x**4 - 3 * x**3 + 2

def grad(x):
    return 4 * x**3 - 9 * x**2

# 初始化参数
x = 6  # 初始点
learning_rate = 0.01
momentum = 0.9
velocity = 0
num_iterations = 100

# 存储优化过程中的值
x_values = []
func_values = []

# 动量法优化
for i in range(num_iterations):
    grad_val = grad(x)
    velocity = momentum * velocity - learning_rate * grad_val
    x += velocity
    
    x_values.append(x)
    func_values.append(func(x))

# 绘制优化过程中的函数值变化
plt.figure(figsize=(14, 6))

plt.subplot(1, 2, 1)
plt.plot(func_values, 'b-o')
plt.title('Function Value during Optimization')
plt.xlabel('Iteration')
plt.ylabel('Function Value')

plt.subplot(1, 2, 2)
plt.plot(x_values, 'r-o')
plt.title('x Value during Optimization')
plt.xlabel('Iteration')
plt.ylabel('x Value')

plt.tight_layout()
plt.show()

# 绘制函数和优化轨迹
x_range = np.linspace(-2, 8, 400)
y_range = func(x_range)

plt.figure(figsize=(10, 6))
plt.plot(x_range, y_range, label='Function: $x^4 - 3x^3 + 2$')
plt.scatter(x_values, func_values, color='red', label='Optimization Path', zorder=5)
plt.plot(x_values, func_values, 'r-o', zorder=5)
plt.title('Optimization Path on the Function')
plt.xlabel('x')
plt.ylabel('Function Value')
plt.legend()
plt.show()

代码解析

1. 函数和梯度的定义：我们定义了一个复杂的函数 f(x) = x4−3x3+2 及其梯度 ∇f(x) = 4x3−9x2。
2. 初始化参数：我们设置了初始点 x=6、学习率 α = 0.01、动量系数 β = 0.9 和速度 v = 0。
3. 优化过程：我们在迭代过程中更新参数值，并记录每次迭代的参数值和函数值。
4. 绘图：

• • 第一个图显示了优化过程中函数值的变化。
  • 第二个图显示了优化过程中 xxx 值的变化。
  • 第三个图显示了函数的曲线和优化轨迹。

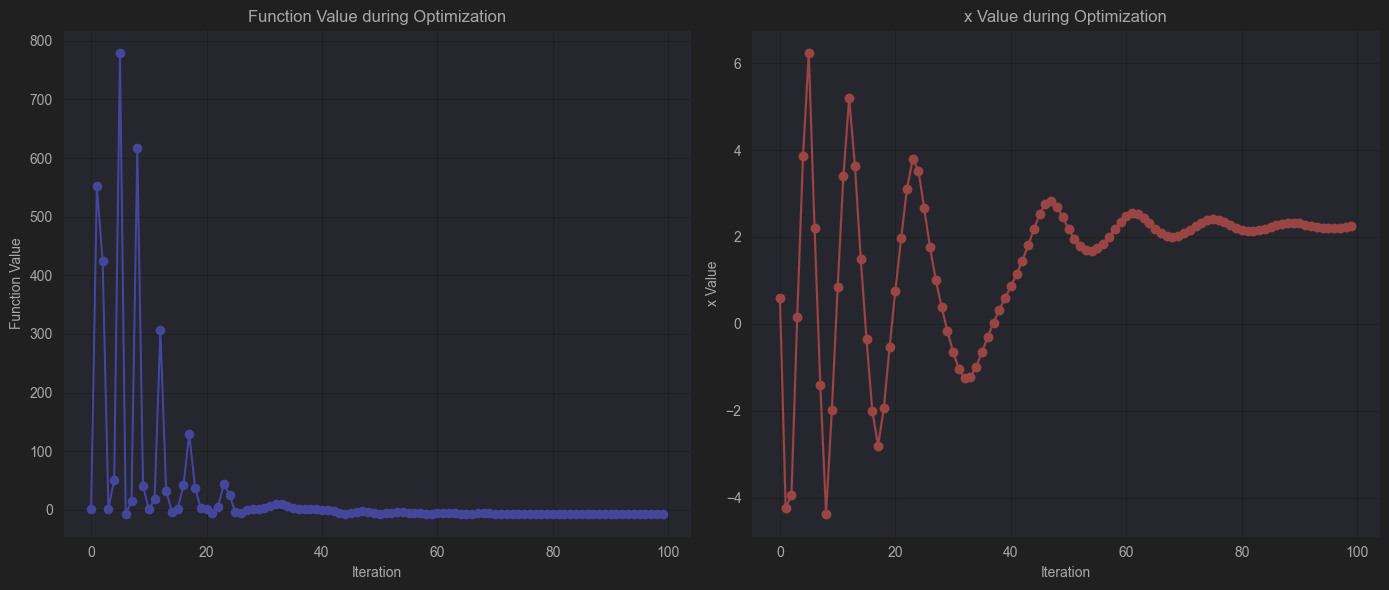
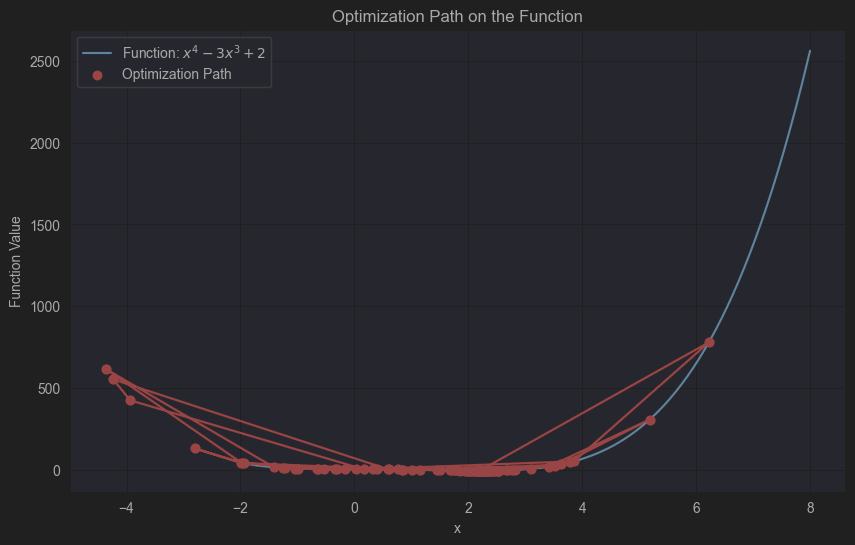
这些图形展示了动量法在优化复杂函数时的效果，可以看到优化轨迹逐步接近函数的最小值点。

生活场景案例：优化物流公司的运输路径

假设我们要优化一个物流公司的运输路径，使得运输成本最小化。这里的运输成本可以看作是一个复杂的函数，我们需要找到使这个成本最小的路径。动量法在这种情况下可以帮助我们更快地找到最优路径，并减少在搜索过程中出现的震荡。

物流公司运输路径优化的场景描述

在物流公司的运输过程中，有多个仓库和多个配送点。我们的目标是找到最优的运输路径，以最小化运输成本。运输成本可以由以下因素决定：

1. 每条路径的距离。
2. 每条路径的交通情况。
3. 每条路径的燃料消耗。

为了简化问题，我们假设运输成本仅由路径的距离决定。我们可以将这个问题抽象为一个数学优化问题，其中运输成本是路径距离的函数。我们需要找到使运输成本最小的路径。

动量法优化物流路径的代码示例

import numpy as np
import matplotlib.pyplot as plt

# 定义运输成本函数及其梯度
# 假设运输成本是路径距离的平方
def cost_function(x):
    return np.sum(x**2)

def gradient(x):
    return 2 * x

# 初始化参数
np.random.seed(42)
num_warehouses = 5
num_delivery_points = 5
initial_path = np.random.rand(num_warehouses + num_delivery_points)  # 初始路径
learning_rate = 0.01
momentum = 0.9
velocity = np.zeros_like(initial_path)
num_iterations = 100

# 存储优化过程中的值
path_values = []
cost_values = []

# 动量法优化
path = initial_path.copy()
for i in range(num_iterations):
    grad_val = gradient(path)
    velocity = momentum * velocity - learning_rate * grad_val
    path += velocity
    
    path_values.append(path.copy())
    cost_values.append(cost_function(path))

# 绘制优化过程中的成本值变化
plt.figure(figsize=(14, 6))

plt.subplot(1, 2, 1)
plt.plot(cost_values, 'b-o')
plt.title('Cost Value during Optimization')
plt.xlabel('Iteration')
plt.ylabel('Cost Value')

plt.subplot(1, 2, 2)
plt.plot(path_values)
plt.title('Path Values during Optimization')
plt.xlabel('Iteration')
plt.ylabel('Path Values')

plt.tight_layout()
plt.show()

# 绘制运输成本函数和优化轨迹
x_range = np.linspace(-2, 2, 400)
y_range = cost_function(x_range)

plt.figure(figsize=(10, 6))
plt.plot(x_range, y_range, label='Cost Function: $x^2$')
plt.scatter(range(len(cost_values)), cost_values, color='red', label='Optimization Path', zorder=5)
plt.plot(range(len(cost_values)), cost_values, 'r-o', zorder=5)
plt.title('Optimization Path on the Cost Function')
plt.xlabel('Iteration')
plt.ylabel('Cost Value')
plt.legend()
plt.show()

代码解析

1. 运输成本函数和梯度的定义：我们假设运输成本是路径距离的平方，即 f(x)=∑x2，其梯度为 ∇f(x)=2x。
2. 初始化参数：我们随机初始化了一个包含仓库和配送点的初始路径，设置了学习率 α=0.01 和动量系数 β=0.9。
3. 优化过程：我们在迭代过程中更新路径，并记录每次迭代的路径和运输成本值。
4. 绘图：

• • 第一个图显示了优化过程中运输成本的变化。
  • 第二个图显示了优化过程中路径的变化。
  • 第三个图显示了运输成本函数和优化轨迹。

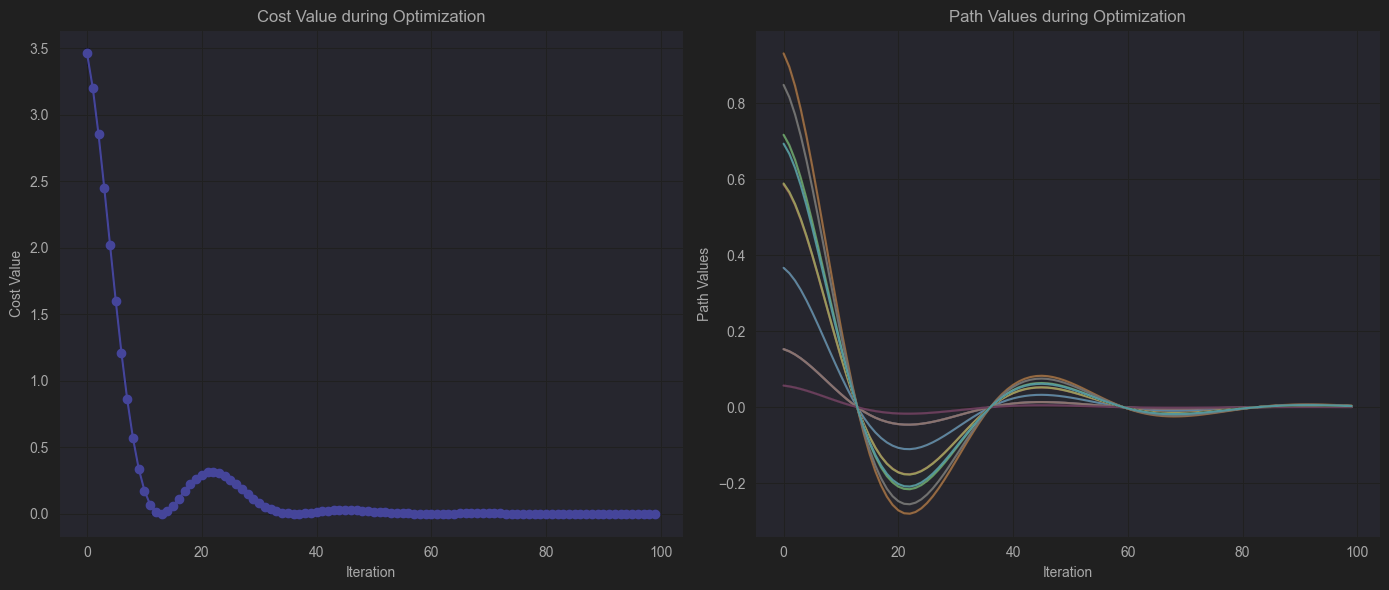
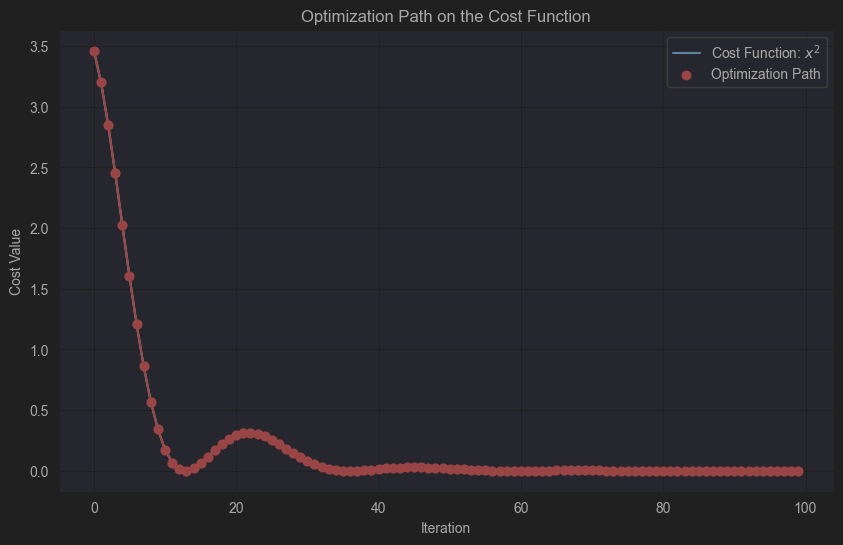
这些图形展示了动量法在优化运输路径时的效果，可以看到优化轨迹逐步接近运输成本的最小值点。通过动量法，我们可以更快地找到最优路径，并减少在搜索过程中出现的震荡，从而有效地降低运输成本。

总结

动量法通过在梯度下降中引入动量项，能够加速收敛，并减少更新过程中的震荡。这使得动量法在许多优化问题中表现出色，尤其是在复杂函数的优化中。通过直观的图形展示，我们可以更好地理解动量法的优化过程和效果。