强化学习（RLAI）读书笔记第十二章资格迹（Eligibility Traces）

最新推荐文章于 2021-12-09 10:33:36 发布

VIP文章无所知

最新推荐文章于 2021-12-09 10:33:36 发布

阅读量7k

点赞数 5

分类专栏：强化学习文章标签： RLAI

本文链接：https://blog.csdn.net/qq_25037903/article/details/82756629

版权

资格迹是强化学习算法中的一个基本机制。比如很流行的 $TD(\lambda)$ 其中的 $\lambda$ 指的就是资格迹的使用。基本上所有的TD算法都能够和资格迹进行组合从而得到一个更通用的算法。资格迹把TD和MC方法统一了起来。当TD算法和资格迹进行组合使用时，得到了一组从一步TD延伸到MC算法的算法家族。一般中间部分的算法效果比两端的好。资格迹同样提供了一种在线continuing形式的问题上使用MC算法的实现方式。

之前第七章使用n步TD法已经组合过了TD法和MC方法，但是资格迹的方式更加的优雅而且有很大的计算优势。这个机制使用了一个短期记忆的向量，资格迹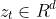 $z_{t}\in R^{d}$ ，与长期的权重w平行。大致的思想是当w的某个分量参与了一个估计值的计算，那么z的相对应的部分就增大，之后慢慢减小。当对应的z分量减小为0之前有一个不为零的TD error，那么w对应的部分就会进行更新。而资格迹消减的系数为 $\lambda$ 。

资格迹相对于n步TD算法的计算优势在于只需要一个资格迹向量而不需要像n步算法一样要保存过去n个状态的特征向量。而学习的过程也连续而均匀均匀分布而不是延迟到获得episode末尾的反馈值为止。另外，学习过程可以每一步都进行从而立马就会影响到下一状态的行为而不是等到n步之后才能更新。

有些算法需要等待之后状态的返回值来进行学习，比如MC算法和n步TD算法。这种基于从被更新状态往前观察的机制叫做forward views。forward views一般都实现起来比较复杂因为需要考虑当前无法获得的之后状态的反馈值。而这一章我们介绍的算法将要能够使用当前的TD error并且通过资格迹使用先前访问过的状态来获得和forward views几乎一样的更新。这种形式叫做backward views。

像往常一样先介绍状态值函数估计，然后延伸到动作值函数和control算法。主要关注线性函数逼近，因为它使用了资格迹的结果会变得更好。线性的结果也可以应用到表格型和状态集成里去。

12.1 The $\lambda$ -return

第七章定义了n步反馈为前n个奖励加上第n步状态的估计值，每一项都加上discounted系数，也就是：

现在考虑更新目标不仅仅是一个n步反馈值，而是不同的n的n步反馈的平均值。比如一个两步反馈的一半加上一个四步反馈的一半组合成的一个新的反馈值。任意的n步反馈的集合可以通过这种形式进行平均，只要最终的系数和为1。合成的反馈值能够和单个的n步反馈一样处理TD error因此能够作为一个保证算法收敛的更新目标。这种平均的形式能够得到一系列新的算法。比如可以通过将一步TD的反馈和无穷步反馈MC反馈进行平均得到一种新的组合TD算法和MC算法的方式。理论上甚至可以将基于模型得到的DP反馈和实际经验得到的反馈进行简单的结合。

这种平均更简单的更新分量的更新叫做复合更新。它的backup diagrams如右图。一个复合更新只能够等待它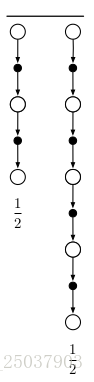的分量中最长的部分更新得到结果之后才能够进行计算。比如右图中的两个更新必须等待t+4的那个更新得到了之后才能计算平均的复合更新。所以使用的时候应该限制最长n步反馈的n，防止每次更新需要过长的等待时间。

$TD(\lambda)$ 算法可以被理解为一种特殊的平均n步更新的形式。这个平均包括了所有的n步更新，每一个的更新的系数都正比于 $\lambda$ ，而所有的系数之和为1;。得到的平均之后的反馈值叫做 $\lambda$ -return：

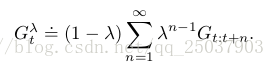
下图显示了每一步反馈值的系数：

对于episode形式的反馈，我们可以将前面的反馈同最后一步的反馈分开，即为：

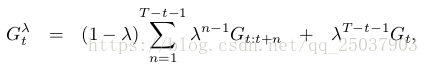
这个形式使得在系数为1的时候更加清楚反馈就是MC形式的反馈。而对于系数为0的时候反馈即为一步TD的反馈。

练习12.1

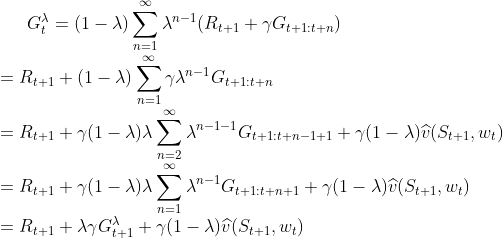
$G_{t}^{\lambda} = (1-\lambda)\sum_{n=1}^{\infty}\lambda^{n-1}(R_{t+1}+\gamma G_{t+1:t+n})\\=R_{t+1}+(1-\lambda)\sum_{n=1}^{\infty}\gamma \lambda^{n-1}G_{t+1:t+n}\\=R_{t+1}+\gamma(1-\lambda)\lambda\sum_{n=2}^{\infty}\lambda^{n-1-1}G_{t+1:t+n-1+1}+\gamma(1-\lambda)\widehat{v}(S_{t+1},w_{t})\\=R_{t+1}+\gamma(1-\lambda)\lambda\sum_{n=1}^{\infty}\lambda^{n-1}G_{t+1:t+n+1}+\gamma(1-\lambda)\widehat{v}(S_{t+1},w_{t})\\=R_{t+1}+\lambda\gamma G_{t+1}^{\lambda}+\gamma(1-\lambda)\widehat{v}(S_{t+1},w_{t})$

练习12.2

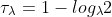
$\tau_{\lambda}=1-log_{\lambda}2$

现在准备定义一个基于 $\lambda$ -return的学习算法：the offline $\lambda$ -return algorithm。作为一个线下算法，在遍历episode的时候不会改变系数w的值，等到episode结尾，一整个序列的更新都根据之前的半梯度法来进行系数的更新：

这个

最低0.47元/天解锁文章

无所知

关注

5
点赞
踩
21

收藏

觉得还不错? 一键收藏
0
评论
强化学习（RLAI）读书笔记第十二章资格迹（Eligibility Traces）

资格迹是强化学习算法中的一个基本机制。比如很流行的其中的指的就是资格迹的使用。基本上所有的TD算法都能够和资格迹进行组合从而得到一个更通用的算法。资格迹把TD和MC方法统一了起来。当TD算法和资格迹进行组合使用时，得到了一组从一步TD延伸到MC算法的算法家族。一般中间部分的算法效果比两端的好。资格迹同样提供了一种在线continuing形式的问题上使用MC算法的实现方式。之前第七章使用n步TD...
复制链接

扫一扫