☞ ░ 前往老猿Python博客 https://blog.csdn.net/LaoYuanPython ░
1、无穷大、无穷小的定义
定义1 :如果函数f(x)当x一>x0(或x一>∞)时的极限为零,那么称函数
f(x)为当x一>x0(或x一>∞)时的无穷小。
特别地,以零为极限的数列{xn}称为n一>∞时的无穷小。
定理1 :在自变量的同一变化过程x一>x0(或x一>∞)中,函数f(x)具有极限A的充分必要条件是f(x)=A+α,其中α是无穷小。
定义2: 设函数f(x)在x的某一去心邻域内有定义(或|x|大于某一正数时有定义)。如果对于任意给定的正数M(不论它多么大),总存在正数δ(或正数X),只要x适合不等式0<lx-x0l<δ(或|x|>X),对应的函数值f(x)总满足不等式
|f(x)|>M.
那么称函数f(x)是当x一>x0(或x一>∞)时的无穷大。
定理2:在自变量的同一变化过程中,如果f(x)为无穷大,那么1/f(x)为无穷小;反之,如果f(x)为无穷小,且f(x)≠0,那么1/f(x)为无穷大。
2、无穷小的大小比较
下面就无穷小之比的极限存在或为无穷大时,来说明两个无穷小之间的比。应当注意,下面的α及β都是在同一个自变量的变化过程中的无穷小,且α≠0,limβ/α也是在这个变化过程中的极限。
定义:
如果 lim β/α=0,那么就说β是比α高阶的无穷小,记作β=o(α)
如果lim β/α=∞,那么就说β是比α低阶的无穷小
如果 lim β/α=c≠0,那么就说β是比α是同阶无穷小
如果lim β/αk=c≠0,k>0,那么就说β是关于α的k阶无穷小
如果lim β/α=1,那么就说B与a是等价无穷小,记作 a~B
定理3:α与β是等价无穷小的充要条件是:β = α+o(α)
定理4:设a1、a2、b1、b2为无穷小,如果a1~a2且b1~b2,且lim a2/b2存在,则
lim a1/b1 = lim a2/b2。即两个无穷小之比的极限,可以将分子分母都用等价无穷小来代替,如果使用得当,可以简化计算。
3、无穷大的大小排列
n、a1、a2、a3为自然数(表述为n∈N),n趋于无穷大(n→∞),a1、a2、a3大于1,则下列实数的大小排列为:
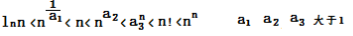
4、 无穷小的大小排列
将无穷大的大小排列公式中比较的数字作为分母,1作为分子,大于号改为小于号,则可以作为无穷小大小排列公式:
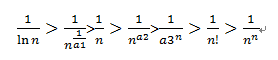
5、极限值
n为自然数(表述为n∈N),n趋于无穷大(n→∞),a2、a3大于1,则下列极限值为0:
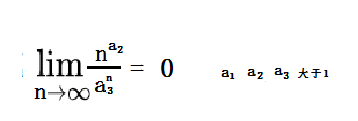
6、斯特林公式(Stirling’s approximation)
斯特林公式(Stirling’s approximation)是一条用来取n的阶乘的近似值的数学公式。公式如下:

斯特林公式(Stirling’s approximation)是一条用来取n的阶乘的近似值的数学公式。一般来说,当n很大的时候,n阶乘的计算量十分大,所以斯特林公式十分好用,而且,即使在n很小的时候,斯特林公式的取值已经十分准确。
写作不易,敬请支持:
如果觉得本文可以给您带来帮助,请大家点击下面的一键三连帮忙点个赞、加个收藏,谢谢!
关于老猿的付费专栏
老猿的付费专栏《使用PyQt开发图形界面Python应用 》(https://blog.csdn.net/laoyuanpython/category_9607725.html)专门介绍基于Python的PyQt图形界面开发基础教程,付费专栏《moviepy音视频开发专栏》 (https://blog.csdn.net/laoyuanpython/category_10232926.html)详细介绍moviepy音视频剪辑合成处理的类相关方法及使用相关方法进行相关剪辑合成场景的处理,两个专栏都适合有一定Python基础但无相关知识的小白读者学习。
付费专栏文章目录:《moviepy音视频开发专栏文章目录》(https://blog.csdn.net/LaoYuanPython/article/details/107574583)、《使用PyQt开发图形界面Python应用专栏目录 》(https://blog.csdn.net/LaoYuanPython/article/details/107580932)。
对于缺乏Python基础的同仁,可以通过老猿的免费专栏《专栏:Python基础教程目录》(https://blog.csdn.net/laoyuanpython/category_9831699.html)从零开始学习Python。
如果有兴趣也愿意支持老猿的读者,欢迎购买付费专栏。

























 2415
2415











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










