本文仅供学习使用
本文参考:
《机构运动微分几何学分析与综合》-王德伦、汪伟
《微分几何》吴大任
0. 前言
- 以微分几何学(标架微分运动)考察刚体连续运动轨迹的局部性质,梳理了刚体平面和球面运动几何学,并发展到空间运动几何学,形成了刚体运动微分几何学理论体系。以鞍点规划方法评价刚体离散运动轨迹的整体性质,从不变量与不变式的视角讨论刚体离散运动几何学,建立了平面、球面和空间机构离散运动鞍点综合的统一方法。
- 刚体运动几何学研究瞬时连续运动轨迹的局部性质和离散运动轨迹的整体性质,常用的方法是几何法与代数法。刚体瞬时运动几何学本是刚体瞬时运动学与图形几何学的结合,理应是从运动视角研究图形的几何性质,而刚体瞬时微小运动则可视为标架微分。
- 微分几何学是用微分方法研究图形性质的数学分支,微分几何学以矢量代数和矢量解析为基本手段,以活动标架为基本方法,把图形的几何形状与所研究的点或线在图形上的运动有机地联系起来,得到图形的不变量和不变式,并以其描述图形的性质。通过把复杂图形的不变量和不变式与简单、规范图形的不变量和不变式相比较,从差异中把握所研究复杂图形的性质。刚体运动的动定瞬轴面(瞬心线)与运动刚体上点(线)轨迹、约束曲线(曲面)的不变量及不变式关系(广义曲率),建立了平面、球面到空间的刚体运动微分几何学理论体系。而关于图形(曲线、曲面)的矢量方程、不变量和不变式、活动标架以及相伴曲线与曲面方法等,形成了本书的微分几何学语言,贯穿全书的始终。
- 作者采用约束曲线与约束曲面的不变量与不变式,通过鞍点规划使离散轨迹与约束曲线、曲面整体比较的最大误差最小,建立刚体离散运动相关位置的约束曲线、曲面对应关系,从不变量与不变式的视角讨论刚体离散运动几何学,从而建立了平面、球面和空间机构离散运动鞍点综合的统一方法。由于以最大拟合误差极小为评价标准,得到统一的法向误差评价体系,对各类曲线、曲面评价拟合准确一致,加之采用不变量,使得求解迭代过程中每一步拟合误差评价在目标函数上都能体现每个变量的实际影响。同时,由于曲线、曲面误差评价拟合的非线性性质,使得机构近似综合解的存在性和局部迭代收敛性得到保证,结合遗传算法可以得到较大范围的局部最优解。
- 本书系统地介绍了刚体运动微分几何学理论体系及机构离散运动鞍点综合的统一方法,为机构运动几何分析与综合方法能够在工程实践中应用提供了理论基础。
1. 平面运动微分几何学
- 平面运动几何学研究图形或刚体平面运动位移的几何性质,即运动刚体上点、线在固定坐标系中轨迹的几何性质,而此处的运动是指刚体占据一系列位置,不涉及具体的时间长短。运动刚体占据位置有连续的,也有分离的,前者称为无限接近位置的运动几何学或瞬时运动几何学,后者称为有限分离位置的运动几何学或离散运动几何学,它们是机构运动综合的理论基础,在机构学研究中具有重要地位。本章仅讨论前者,后者在下一章论述。
- 但对于刚体运动学与轨迹图形几何学性质及其相互联系的研究,还是现代微分几何学方法见长,不仅采用不变量与不变式刻画几何学性质,消除坐标系影响,从而使表达式简洁明了,同时以活动标架方式将运动学与几何学联系起来,以运动方式研究几何学问题,尤其是三维空间乃至多维空间运动几何学,更彰显微分几何学方法的优势。
1.1 平面曲线微分几何学
1.1.1 平面曲线微分几何学
-
对于平面曲线 Γ \Gamma Γ存在直角坐标参数: { x = x ( t ) y = y ( t ) \left\{ \begin{matrix} x=x(t) \\ y=y(t) \\ \end{matrix} \right. {x=x(t)y=y(t),其中: t t t为曲线参数,上式消去/置换参数 t t t可得关系表达式: y = F ( x ) y=F(x) y=F(x),可得坐标参数的隐函数形式: F ( x , y ) = 0 F(x,y)=0 F(x,y)=0。
将上述坐标参数置于坐标系 { O : i ⃗ , j ⃗ } \{O:\vec{i},\vec{j}\} {O:i,j}中,则可得曲线 Γ \Gamma Γ的矢量方程: Γ : R ⃗ = x ( t ) i ⃗ + y ( t ) j ⃗ \Gamma :\vec{R}=x(t)\vec{i}+y(t)\vec{j} Γ:R=x(t)i+y(t)j,或简化为: Γ : R ⃗ = R ⃗ ( t ) \Gamma :\vec{R}=\vec{R}(t) Γ:R=R(t),其中: t t t为曲线参数。 -
在平面坐标系 { O : i ⃗ , j ⃗ } \{O:\vec{i},\vec{j}\} {O:i,j}中,与 i i i轴夹 φ \varphi φ角的单位矢量函数: e ⃗ I ( φ ) {{{\vec{e}}}_{I(\varphi )}} eI(φ)称为
圆矢量函数,将平面曲线 Γ \Gamma Γ用圆矢量表示为: R ⃗ = r ( φ ) e ⃗ I ( φ ) \vec{R}=r(\varphi ){{{\vec{e}}}_{I(\varphi )}} R=r(φ)eI(φ),其中: r ( φ ) r(\varphi ) r(φ)决定 R ⃗ {\vec{R}} R的大小, e ⃗ I ( φ ) {{{\vec{e}}}_{I(\varphi )}} eI(φ)决定 R ⃗ {\vec{R}} R的方向。
若将 e ⃗ I ( φ ) {{{\vec{e}}}_{I(\varphi )}} eI(φ)绕单位矢量 k k k逆时针转动90°,可得圆矢量 e ⃗ I I ( φ ) = e ⃗ I ( φ + π / 2 ) {{{\vec{e}}}_{II(\varphi )}}={{{\vec{e}}}_{I(\varphi +\pi /2)}} eII(φ)=eI(φ+π/2)

圆矢量具有如下性质(易证):
1. 展开式:
{ e ⃗ I ( φ ) = cos φ i ⃗ + sin φ j ⃗ e ⃗ I I ( φ ) = − sin φ i ⃗ + cos φ j ⃗ \left\{ \begin{matrix} {{{\vec{e}}}_{I(\varphi )}}=\cos \varphi \vec{i}+\sin \varphi \vec{j} \\ {{{\vec{e}}}_{II(\varphi )}}=-\sin \varphi \vec{i}+\cos \varphi \vec{j} \\ \end{matrix} \right. {eI(φ)=cosφi+sinφjeII(φ)=−sinφi+cosφj
2. 正交性:
约定 { O : e ⃗ I ( φ ) , e ⃗ I I ( φ ) , k ⃗ } \{O:{{{\vec{e}}}_{I(\varphi )}},{{{\vec{e}}}_{II(\varphi )}},\vec{k}\} {O:eI(φ),eII(φ),k}构成单位正交右手系,即: e ⃗ I ( φ ) ⋅ e ⃗ I I ( φ ) = 0 {{{\vec{e}}}_{I(\varphi )}}\cdot {{{\vec{e}}}_{II(\varphi )}}=0 eI(φ)⋅eII(φ)=0, e ⃗ I ( φ ) × e ⃗ I I ( φ ) = k ⃗ {{{\vec{e}}}_{I(\varphi )}}\times {{{\vec{e}}}_{II(\varphi )}}=\vec{k} eI(φ)×eII(φ)=k
3. 合角公式:
{ e ⃗ I ( θ + φ ) = cos ( θ + φ ) i ⃗ + sin ( θ + φ ) j ⃗ = cos θ e ⃗ I ( φ ) + sin θ e ⃗ I I ( φ ) e ⃗ I I ( θ + φ ) = − sin ( θ + φ ) i ⃗ + cos ( θ + φ ) j ⃗ = − sin θ e ⃗ I ( φ ) + cos θ e ⃗ I I ( φ ) \left\{ \begin{matrix} {{{\vec{e}}}_{I(\theta +\varphi )}}=\cos (\theta +\varphi )\vec{i}+\sin (\theta +\varphi )\vec{j}=\cos \theta {{{\vec{e}}}_{I(\varphi )}}+\sin \theta {{{\vec{e}}}_{II(\varphi )}} \\ {{{\vec{e}}}_{II(\theta +\varphi )}}=-\sin (\theta +\varphi )\vec{i}+\cos (\theta +\varphi )\vec{j}=-\sin \theta {{{\vec{e}}}_{I(\varphi )}}+\cos \theta {{{\vec{e}}}_{II(\varphi )}} \\ \end{matrix} \right. {eI(θ+φ)=cos(θ+φ)i+sin(θ+φ)j=cosθeI(φ)+sinθeII(φ)eII(θ+φ)=−sin(θ+φ)i+cos(θ+φ)j=−sinθeI(φ)+cosθeII(φ)
4. 微分公式:
d e ⃗ I ( φ ) d φ = e ⃗ I I ( φ ) , d e ⃗ I I ( φ ) d φ = − e ⃗ I ( φ ) \frac{d{{{\vec{e}}}_{I(\varphi )}}}{d\varphi }={{{\vec{e}}}_{II(\varphi )}},\frac{d{{{\vec{e}}}_{II(\varphi )}}}{d\varphi }=-{{{\vec{e}}}_{I(\varphi )}} dφdeI(φ)=eII(φ),dφdeII(φ)=−eI(φ)
例1-1 用圆矢量函数表示圆的矢量方程:
圆在平面直角坐标系 { O : i ⃗ , j ⃗ } \{O:\vec{i},\vec{j}\} {O:i,j}中的方程为:
{ x = x c + r cos φ y = y c + r sin φ ( 0 ≤ φ < 2 π ) \left\{ \begin{matrix} x={{x}_{c}}+r\cos \varphi \\ y={{y}_{c}}+r\sin \varphi \\ \end{matrix} \right.(0\le \varphi <2\pi ) {x=xc+rcosφy=yc+rsinφ(0≤φ<2π),其中 r r r为圆的半径, ( x c , y c ) ({{x}_{c}},{{y}_{c}}) (xc,yc)为圆心 C C C在坐标系 { O : i ⃗ , j ⃗ } \{O:\vec{i},\vec{j}\} {O:i,j}中的坐标。
若采用圆矢量函数表示圆的矢量方程,则有:
R ⃗ = R ⃗ C + r e ⃗ I ( φ ) \vec{R}={{{\vec{R}}}_{C}}+r{{{\vec{e}}}_{I(\varphi )}} R=RC+reI(φ)
例1-2 用圆矢量函数表示渐开线的矢量方程:
渐开线在极坐标系中的坐标参数为:
{ r = r b cos α θ = tan α − α \left\{ \begin{matrix} r=\frac{{{r}_{b}}}{\cos \alpha } \\ \theta =\tan \alpha -\alpha \\ \end{matrix} \right. {r=cosαrbθ=tanα−α
在直角坐标系中的坐标参数为:
{ x = r b cos φ + r b φ sin φ y = r b sin φ − r b φ cos φ \left\{ \begin{matrix} x={{r}_{b}}\cos \varphi +{{r}_{b}}\varphi \sin \varphi \\ y={{r}_{b}}\sin \varphi -{{r}_{b}}\varphi \cos \varphi \\ \end{matrix} \right. {x=rbcosφ+rbφsinφy=rbsinφ−rbφcosφ
若采用圆矢量函数表达渐开线的矢量方程,则有:
R ⃗ = r b e ⃗ I ( φ ) − r b e ⃗ I I ( φ ) \vec{R}={{r}_{b}}{{{\vec{e}}}_{I(\varphi )}}-{{r}_{b}}{{{\vec{e}}}_{II(\varphi )}} R=rbeI(φ)−rbeII(φ)
例1-3:用圆矢量函数表示平面全铰链四连杆机构连杆的曲线矢量方程:
建立连杆坐标系: { B : i ⃗ m , j ⃗ m } \{B:{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\} {B:im,jm},机架固定坐标系: { A : i ⃗ f , j ⃗ f } \{A:{{{\vec{i}}}_{f}},{{{\vec{j}}}_{f}}\} {A:if,jf},点P在连杆上极坐标坐标参数为: ( r p , θ p ) ({{r}_{p}},{{\theta }_{p}}) (rp,θp):
- 点P在连杆坐标系 { B : i ⃗ m , j ⃗ m } \{B:{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\} {B:im,jm}的坐标为: { x m = r p cos θ p y m = r p sin θ p \left\{ \begin{matrix} {{x}_{m}}={{r}_{p}}\cos {{\theta }_{p}} \\ {{y}_{m}}={{r}_{p}}\sin {{\theta }_{p}} \\ \end{matrix} \right. {xm=rpcosθpym=rpsinθp
- 通过坐标变换可得P在固定坐标系 { A : i ⃗ f , j ⃗ f } \{A:{{{\vec{i}}}_{f}},{{{\vec{j}}}_{f}}\} {A:if,jf}的轨迹曲线的坐标参数为: { x = r p cos ( θ p + γ ) + a 1 cos φ y = r p sin ( θ p + γ ) + a 1 sin φ \left\{ \begin{matrix} x={{r}_{p}}\cos ({{\theta }_{p}}+\gamma )+{{a}_{1}}\cos \varphi \\ y={{r}_{p}}\sin ({{\theta }_{p}}+\gamma )+{{a}_{1}}\sin \varphi \\ \end{matrix} \right. {x=rpcos(θp+γ)+a1cosφy=rpsin(θp+γ)+a1sinφ
用圆矢量函数 e ⃗ I ( φ ) {{{\vec{e}}}_{I(\varphi )}} eI(φ)表示B点的位移矢量,圆矢量函数 e ⃗ I ( θ p + γ ) {{{\vec{e}}}_{I({{\theta }_{p}}+\gamma )}} eI(θp+γ)表示P点相对于B点的位移矢量,则机构的连杆曲线的矢量方程为:
R ⃗ P = a 1 e ⃗ I ( φ ) + r p e ⃗ I ( θ p + γ ) {{{\vec{R}}}_{P}}={{a}_{1}}{{{\vec{e}}}_{I(\varphi )}}+{{r}_{p}}{{{\vec{e}}}_{I({{\theta }_{p}}+\gamma )}} RP=a1eI(φ)+rpeI(θp+γ)
根据上述例子可见,采用圆矢量函数对平面曲线进行矢量表达,不但使得表达式简洁,更重要的是,由于圆矢量函数固有的性质,使得对平面曲线矢量方程的求导等计算更为简便。
微分几何学指出:曲线的不变量与所选择的坐标系无关,以弧长 s s s为例:是曲线的不变量,被称为曲线的自然参数,弧长 s s s在直角坐标系的表达式中建立与参数 t t t的关系为: d s = ∣ d R ⃗ ∣ = ( d x d t ) 2 + ( d y d t ) 2 d t , s = ∫ t a t b ∣ d R ⃗ d t ∣ d t ds=\left| d\vec{R} \right|=\sqrt{{{(\frac{dx}{dt})}^{2}}+{{(\frac{dy}{dt})}^{2}}}dt,s=\int_{{{t}_{a}}}^{{{t}_{b}}}{\left| \frac{d\vec{R}}{dt} \right|}dt ds= dR =(dtdx)2+(dtdy)2dt,s=∫tatb dtdR dt。若把曲线 Γ \Gamma Γ的矢量方程用弧长参数 s s s表示: Γ : R ⃗ = R ⃗ ( s ) , s a ≤ s ≤ s b \Gamma :\vec{R}=\vec{R}(s),{{s}_{a}}\le s\le {{s}_{b}} Γ:R=R(s),sa≤s≤sb。由于 d s = ∣ d R ⃗ ∣ ds=\left| d\vec{R} \right| ds= dR ,即 ∣ d R ⃗ d s ∣ = 1 \left| \frac{d\vec{R}}{ds} \right|=1 dsdR =1,若把曲线 Γ \Gamma Γ放在某点 s s s的邻域 Δ s \Delta s Δs内进行泰勒展开,则有: R ⃗ ( s + Δ s ) = R ⃗ ( s ) + d R ⃗ ( s ) d s Δ s + 1 2 ! d 2 R ⃗ ( s ) d s 2 ( Δ s ) 2 + . . . + 1 n ! d n R ⃗ ( s ) d s n ( Δ s ) n + ε n ( s , Δ s ) ( Δ s ) n \vec{R}(s+\Delta s)=\vec{R}(s)+\frac{d\vec{R}(s)}{ds}\Delta s+\frac{1}{2!}\frac{{{d}^{2}}\vec{R}(s)}{d{{s}^{2}}}{{(\Delta s)}^{2}}+...+\frac{1}{n!}\frac{{{d}^{n}}\vec{R}(s)}{d{{s}^{n}}}{{(\Delta s)}^{n}}+{{\varepsilon }_{n}}(s,\Delta s){{(\Delta s)}^{n}} R(s+Δs)=R(s)+dsdR(s)Δs+2!1ds2d2R(s)(Δs)2+...+n!1dsndnR(s)(Δs)n+εn(s,Δs)(Δs)n,其中: lim ε n ( s , Δ s ) = 0 \lim {{\varepsilon }_{n}}(s,\Delta s)=0 limεn(s,Δs)=0。
1.1.2 Frenet标架
- 平面曲线
R
⃗
=
R
⃗
(
s
)
\vec{R}=\vec{R}(s)
R=R(s)的单位切矢
α
⃗
=
d
R
⃗
(
s
)
d
s
\vec{\alpha }=\frac{d\vec{R}(s)}{ds}
α=dsdR(s)始终指向曲线弧长增加的方向,依旧坐标轴正交右手系约定,定义法线矢量
β
⃗
{\vec{\beta }}
β,即
β
⃗
=
k
⃗
×
α
⃗
\vec{\beta }=\vec{k}\times \vec{\alpha }
β=k×α,从而构件平面曲线的右手坐标系
{
R
⃗
:
α
⃗
,
β
⃗
}
\{\vec{R}:\vec{\alpha },\vec{\beta }\}
{R:α,β},即
Frenet标架(也称活动标架)。 - 由于利用了曲线本身的切线与法线,因而与曲线的几何性质建立了密切联系,且其微分运算公式为:
{ d R ⃗ ( s ) d s = α ⃗ d α ⃗ d s = k β ⃗ d β ⃗ d s = − k α ⃗ \left\{ \begin{matrix} \frac{d\vec{R}(s)}{ds}=\vec{\alpha } \\ \frac{d\vec{\alpha }}{ds}=k\vec{\beta } \\ \frac{d\vec{\beta }}{ds}=-k\vec{\alpha } \\ \end{matrix} \right. ⎩ ⎨ ⎧dsdR(s)=αdsdα=kβdsdβ=−kα(也称为平面曲线的Frenet公式,其中 k k k为平面曲线的曲率)

- 曲率 k k k的表达式为: k = d α ⃗ d s ⋅ β ⃗ = ( d α ⃗ d s , k ⃗ × α ⃗ ) = ( k ⃗ , d R ⃗ ( s ) d s , d 2 R ⃗ ( s ) d s 2 ) k=\frac{d\vec{\alpha }}{ds}\cdot \vec{\beta }=(\frac{d\vec{\alpha }}{ds},\vec{k}\times \vec{\alpha })=(\vec{k},\frac{d\vec{R}(s)}{ds},\frac{{{d}^{2}}\vec{R}(s)}{d{{s}^{2}}}) k=dsdα⋅β=(dsdα,k×α)=(k,dsdR(s),ds2d2R(s))
- 若平面曲线 Γ \Gamma Γ以一般参数矢量形式: R ⃗ = x ( t ) i ⃗ + y ( t ) j ⃗ \vec{R}=x(t)\vec{i}+y(t)\vec{j} R=x(t)i+y(t)j给出,则其曲线切矢 α ⃗ {\vec{\alpha }} α为: α ⃗ = d R ⃗ ( s ) d s = d R ⃗ ( s ) d t ⋅ d t d s = d t d s ( d x d t i ⃗ + d y d t j ⃗ ) \vec{\alpha }=\frac{d\vec{R}(s)}{ds}=\frac{d\vec{R}(s)}{dt}\cdot \frac{dt}{ds}=\frac{dt}{ds}(\frac{dx}{dt}\vec{i}+\frac{dy}{dt}\vec{j}) α=dsdR(s)=dtdR(s)⋅dsdt=dsdt(dtdxi+dtdyj)
- 由 β ⃗ = k ⃗ × α ⃗ \vec{\beta }=\vec{k}\times \vec{\alpha } β=k×α可得曲线法矢量 β ⃗ {\vec{\beta }} β为: β ⃗ = d t d s ( − d y d t i ⃗ + d x d t j ⃗ ) \vec{\beta }=\frac{dt}{ds}(-\frac{dy}{dt}\vec{i}+\frac{dx}{dt}\vec{j}) β=dsdt(−dtdyi+dtdxj),又已知: d t d s = 1 / ( d x d t ) 2 + ( d y d t ) 2 \frac{dt}{ds}=1/\sqrt{{{(\frac{dx}{dt})}^{2}}+{{(\frac{dy}{dt})}^{2}}} dsdt=1/(dtdx)2+(dtdy)2,则曲线 Γ \Gamma Γ的曲率 k k k为: k = d α ⃗ d s ⋅ β ⃗ = d t d s d α ⃗ d t ⋅ β ⃗ = d x d t ⋅ d 2 y d t 2 − d y d t ⋅ d 2 x d t 2 [ ( d x d t ) 2 + ( d y d t ) 2 ] 3 2 k=\frac{d\vec{\alpha }}{ds}\cdot \vec{\beta }=\frac{dt}{ds}\frac{d\vec{\alpha }}{dt}\cdot \vec{\beta }=\frac{\frac{dx}{dt}\cdot \frac{{{d}^{2}}y}{d{{t}^{2}}}-\frac{dy}{dt}\cdot \frac{{{d}^{2}}x}{d{{t}^{2}}}}{{{[{{(\frac{dx}{dt})}^{2}}+{{(\frac{dy}{dt})}^{2}}]}^{\frac{3}{2}}}} k=dsdα⋅β=dsdtdtdα⋅β=[(dtdx)2+(dtdy)2]23dtdx⋅dt2d2y−dtdy⋅dt2d2x
- 在平面固定坐标系 { O : i ⃗ , j ⃗ } \{O:\vec{i},\vec{j}\} {O:i,j}中,切矢 α ⃗ {\vec{\alpha }} α为单位矢量,假设其方向角为 θ \theta θ,则 α ⃗ = cos θ i ⃗ + sin θ j ⃗ , β ⃗ = − sin θ i ⃗ + cos θ j ⃗ \vec{\alpha }=\cos \theta \vec{i}+\sin \theta \vec{j},\vec{\beta }=-\sin \theta \vec{i}+\cos \theta \vec{j} α=cosθi+sinθj,β=−sinθi+cosθj,将切矢 α ⃗ {\vec{\alpha }} α对弧长 s s s求导,可得: d α ⃗ d s = d α ⃗ d θ d θ d s = d θ d s ( − sin θ i ⃗ + cos θ j ⃗ ) = d θ d s β ⃗ \frac{d\vec{\alpha }}{ds}=\frac{d\vec{\alpha }}{d\theta }\frac{d\theta }{ds}=\frac{d\theta }{ds}(-\sin \theta \vec{i}+\cos \theta \vec{j})=\frac{d\theta }{ds}\vec{\beta } dsdα=dθdαdsdθ=dsdθ(−sinθi+cosθj)=dsdθβ
- 即
k
=
d
α
⃗
d
s
⋅
β
⃗
=
d
θ
d
s
β
⃗
⋅
β
⃗
=
d
θ
d
s
k=\frac{d\vec{\alpha }}{ds}\cdot \vec{\beta }=\frac{d\theta }{ds}\vec{\beta }\cdot \vec{\beta }=\frac{d\theta }{ds}
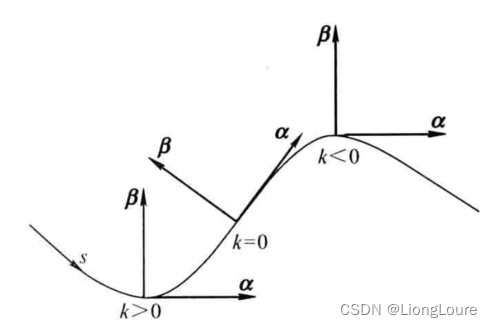
k=dsdα⋅β=dsdθβ⋅β=dsdθ,即平面曲线曲率的几何意义是曲线的切矢量的方向角
θ
\theta
θ关于弧长
s
s
s的变化率,其正负号反映了平面曲线的凹凸变化。当
β
⃗
{\vec{\beta }}
β指向凹入一侧,则
k
>
0
k>0
k>0,反之,
k
<
0
k<0
k<0,而在曲线凹凸的转折点处,曲率
k
=
0
k=0
k=0,称为平面曲线的
拐点。
- 将曲率
k
k
k的倒数
ρ
\rho
ρ称为平面曲线的
曲率半径(同样具有正负号): ρ = 1 k = d s d θ \rho =\frac{1}{k}=\frac{ds}{d\theta } ρ=k1=dθds。对于平面曲线上的点,若曲率半径 ρ ≠ 0 \rho \ne 0 ρ=0,则存在曲率中心,其矢量表达为 R ⃗ C = R ⃗ + ρ ⋅ β ⃗ {{{\vec{R}}}_{C}}=\vec{R}+\rho \cdot \vec{\beta } RC=R+ρ⋅β
定理1.1 在区间 ( s a , s b ) ({{s}_{a}},{{s}_{b}}) (sa,sb)上任意给定一个连续函数 k ( s ) k(s) k(s),同时给定一个初始点(矢量) R ⃗ a {{{\vec{R}}}_{a}} Ra。以及单位矢量 α ⃗ a {{{\vec{\alpha }}}_{a}} αa。,则一定有且仅有一条以 s s s为弧长,以 k ( s ) k(s) k(s)为其曲率的平面有向曲线。
由于曲率
k
k
k是平面曲线的不变量,并且不依赖于所选定的坐标系,便能够唯一地确定平面曲线,因而将
k
=
k
(
s
)
k=k(s)
k=k(s)称为平面曲线的自然方程。平面曲线中,直线和圆是最常见的两种特殊曲线,前者的曲率为零,而后者的曲率则为常数。
-
若平面曲线上一点及其邻域内的曲率为常数,则该平面曲线在该点的局部范围内接近于圆曲线。通常地,两条曲线在某一点的接触阶数可以用来描述两条曲线在该接触点处的逼近程度。若两条平面曲线之间有两个无限接近位置的共同点,则这两条曲线相切接触,可称为
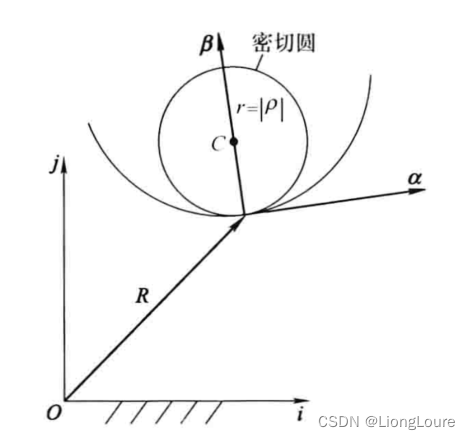
一阶接触。同理,若两条平面曲线之间在无限接近位置有n+1个共同点,则它们形成n阶接触。因此,若一条平面曲线与一圆一阶接触,表明该圆相切于这条平面曲线;而若二阶接触,则它们在无限接近三个位置有共同点,称该圆为这条平面曲线的密切圆,其半径恰为该平面曲线在接触点处曲率半径的绝对值,密切圆也称为曲率圆。若平面曲线与圆三阶接触,或者说它们在无限接近四个位置有共同点,该平面曲线在接触点处的曲率对弧长参数的一阶导数应为零,即 d k d s = 0 \frac{dk}{ds}=0 dsdk=0。类似地,若平面曲线与圆的接触阶数为n,则该平面曲线在接触点处曲率对弧长参数直至n-2阶导数均为零。
-
平面曲线 Γ \Gamma Γ上点P(对应的自然参数为 s s s)处密切圆的圆心矢径为:
Γ C : R ⃗ C = R ⃗ + 1 k β ⃗ {{\Gamma }_{C}}:{{\vec{R}}_{C}}=\vec{R}+\frac{1}{k}\vec{\beta } ΓC:RC=R+k1β
若曲线 Γ \Gamma Γ为一圆,则密切圆中心的曲线 Γ C {{\Gamma }_{C}} ΓC为一固定点,不随自然参数 s s s变化而变化,有 d R ⃗ C d s = d ( 1 / k ) d s β ⃗ = 0 \frac{d{{{\vec{R}}}_{C}}}{ds}=\frac{d(1/k)}{ds}\vec{\beta }=0 dsdRC=dsd(1/k)β=0,即 k k k为常数,曲率圆的半径为常数 -
直线可看作曲率半径趋于无穷大的圆,即 k = 0 k=0 k=0。当平面曲线在一点处与直线形成一阶接触,即该点邻域内无限接近位置两个点在一直线上,则直线即为曲线在该点的切矢所在直线;若曲线在一点处与直线形成二阶接触,则该点邻域内无限接近位置三个点在直线上,也就是曲线在该点的曲率为零,曲线出现拐点;若曲线在一点处与直线形成三阶接触,则该点邻域内无限接近位置四个点在直线上,则曲线在该点的曲率需同时满足 k = 0 k=0 k=0以及 d k d s = 0 \frac{dk}{ds}=0 dsdk=0
平面闭曲线:首尾相接的平面曲线称为平面闭曲线,即 R ⃗ ( s a ) = R ⃗ ( s b ) \vec{R}({{s}_{a}})=\vec{R}({{s}_{b}}) R(sa)=R(sb);
平面简单闭曲线:若平面闭曲线上无自交点,或者说无而充电,则为平面简单闭曲线;
平面凸闭曲线:如果平面简单闭曲线上每处的切矢都在曲线正向的同一侧,则称该简单闭曲线为平面凸闭曲线。(也成为卵形线)
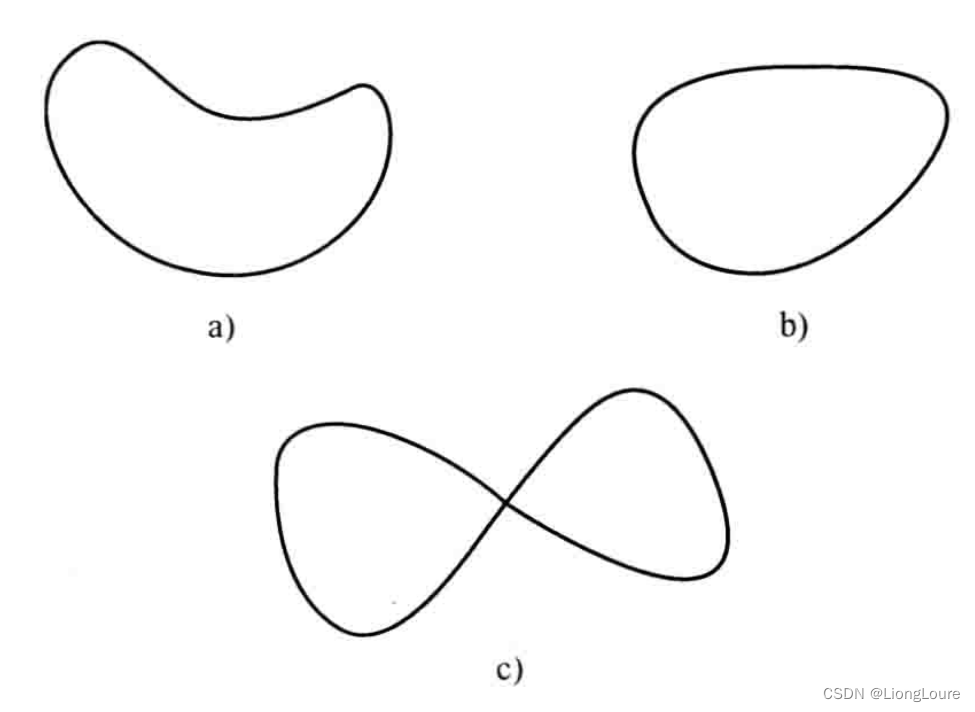
定理1.2 一条平面简单闭曲线为凸闭曲线的充要条件是,适当地选择曲线的正向后,可使曲线上的各点的曲率 k ≥ 0 k\ge 0 k≥0。
如果一条凸闭曲线上各点处的曲率k不等于零,则为卵形线。
推论1 一条平面简单闭曲线,在其正向选定后,曲线上各点的曲率 k k k的符号不变,则该曲线必为卵形线
1.1.3 相伴方法(Cesaro方法)
平面固定坐标系
{
O
:
i
⃗
,
j
⃗
}
\{O:\vec{i},\vec{j}\}
{O:i,j}中有一曲线
Γ
P
{{\Gamma }_{P}}
ΓP,在曲线
Γ
P
{{\Gamma }_{P}}
ΓP外一点
P
∗
P*
P∗伴随着
Γ
P
{{\Gamma }_{P}}
ΓP上的点P运动,形成另一条平面曲线
Γ
P
∗
{{\Gamma }_{P}}*
ΓP∗,称曲线
Γ
P
{{\Gamma }_{P}}
ΓP为原曲线,曲线
Γ
P
∗
{{\Gamma }_{P}}*
ΓP∗为
Γ
P
{{\Gamma }_{P}}
ΓP的相伴曲线。
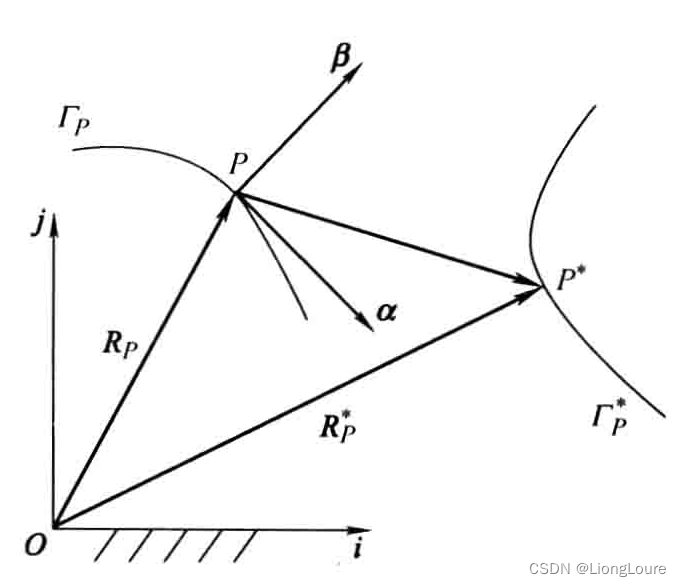
在原曲线
Γ
P
{{\Gamma }_{P}}
ΓP上建立Frenet标架
{
R
⃗
P
:
α
⃗
,
β
⃗
}
\{{{{\vec{R}}}_{P}}:\vec{\alpha },\vec{\beta }\}
{RP:α,β},则相伴曲线
Γ
P
∗
{{\Gamma }_{P}}*
ΓP∗的矢量方程为:
Γ
P
∗
:
R
⃗
P
∗
=
R
⃗
P
+
u
1
α
⃗
+
u
2
β
⃗
{{\Gamma }_{P}}*:{{{\vec{R}}}_{P}}*={{{\vec{R}}}_{P}}+{{u}_{1}}\vec{\alpha }+{{u}_{2}}\vec{\beta }
ΓP∗:RP∗=RP+u1α+u2β
其中:
(
u
1
,
u
2
)
({{u}_{1}},{{u}_{2}})
(u1,u2)为点
P
∗
P*
P∗关于曲线
Γ
P
{{\Gamma }_{P}}
ΓP上
P
P
P点处Frenet标架
{
R
⃗
P
:
α
⃗
,
β
⃗
}
\{{{{\vec{R}}}_{P}}:\vec{\alpha },\vec{\beta }\}
{RP:α,β}的相对坐标(参数)。对上式求导,可得:
{
d
R
⃗
P
∗
d
s
=
A
1
α
⃗
+
A
2
β
⃗
A
1
=
1
+
d
u
1
d
s
−
k
u
2
A
2
=
k
u
1
+
d
u
2
d
s
\left\{ \begin{matrix} \frac{d{{{\vec{R}}}_{P}}*}{ds}={{A}_{1}}\vec{\alpha }+{{A}_{2}}\vec{\beta } \\ {{A}_{1}}=1+\frac{d{{u}_{1}}}{ds}-k{{u}_{2}} \\ {{A}_{2}}=k{{u}_{1}}+\frac{d{{u}_{2}}}{ds} \\ \end{matrix} \right.
⎩
⎨
⎧dsdRP∗=A1α+A2βA1=1+dsdu1−ku2A2=ku1+dsdu2
详细推导:
d R ⃗ P ∗ d s = d u 1 d s α ⃗ + u 1 d α ⃗ d s + d u 2 d s β ⃗ + u 2 d β ⃗ d s + d R ⃗ P d s = d u 1 d s α ⃗ + u 1 k β ⃗ + d u 2 d s β ⃗ + ( − u 2 k α ⃗ ) + α ⃗ \frac{d{{{\vec{R}}}_{P}}*}{ds}=\frac{d{{u}_{1}}}{ds}\vec{\alpha }+{{u}_{1}}\frac{d\vec{\alpha }}{ds}+\frac{d{{u}_{2}}}{ds}\vec{\beta }+{{u}_{2}}\frac{d\vec{\beta }}{ds}+\frac{d{{{\vec{R}}}_{P}}}{ds}=\frac{d{{u}_{1}}}{ds}\vec{\alpha }+{{u}_{1}}k\vec{\beta }+\frac{d{{u}_{2}}}{ds}\vec{\beta }+(-{{u}_{2}}k\vec{\alpha })+\vec{\alpha } dsdRP∗=dsdu1α+u1dsdα+dsdu2β+u2dsdβ+dsdRP=dsdu1α+u1kβ+dsdu2β+(−u2kα)+α
= ( 1 + d u 1 d s − k u 2 ) α ⃗ + ( k u 1 + d u 2 d s ) β ⃗ =(1+\frac{d{{u}_{1}}}{ds}-k{{u}_{2}})\vec{\alpha }+(k{{u}_{1}}+\frac{d{{u}_{2}}}{ds})\vec{\beta } =(1+dsdu1−ku2)α+(ku1+dsdu2)β
其中:
- d R ⃗ P ∗ d s \frac{d{{{\vec{R}}}_{P}}*}{ds} dsdRP∗为平面曲线 Γ P ∗ {{\Gamma }_{P}}* ΓP∗的切线矢量。
- 点 P ∗ P* P∗在固定坐标系 { O : i ⃗ , j ⃗ } \{O:\vec{i},\vec{j}\} {O:i,j}中的绝对运动则可在原曲线 Γ P {{\Gamma }_{P}} ΓP上的Frenet标架 { R ⃗ P : α ⃗ , β ⃗ } \{{{{\vec{R}}}_{P}}:\vec{\alpha },\vec{\beta }\} {RP:α,β}中描述。
- ( d u 1 d s , d u 2 d s ) (\frac{d{{u}_{1}}}{ds},\frac{d{{u}_{2}}}{ds}) (dsdu1,dsdu2)为点 P ∗ P* P∗在活动标架 { R ⃗ P : α ⃗ , β ⃗ } \{{{{\vec{R}}}_{P}}:\vec{\alpha },\vec{\beta }\} {RP:α,β}中的相对坐标(参数)变化率分量。
- ( A 1 , A 2 ) ({{A}_{1}},{{A}_{2}}) (A1,A2)则是点 P ∗ P* P∗在固定坐标系中的坐标(参数)变化率并在活动标架 { R ⃗ P : α ⃗ , β ⃗ } \{{{{\vec{R}}}_{P}}:\vec{\alpha },\vec{\beta }\} {RP:α,β}中描述。
- 当
P
∗
P*
P∗是平面坐标系
{
O
:
i
⃗
,
j
⃗
}
\{O:\vec{i},\vec{j}\}
{O:i,j}中一固定点时,该点绝对坐标并不随原曲线
Γ
P
{{\Gamma }_{P}}
ΓP自然参数弧长s的变化而变化,即绝对运动变化率为零
d
R
⃗
P
∗
d
s
=
0
\frac{d{{{\vec{R}}}_{P}}*}{ds}=0
dsdRP∗=0,则有:
{ A 1 = 1 + d u 1 d s − k u 2 A 2 = k u 1 + d u 2 d s \left\{ \begin{matrix} {{A}_{1}}=1+\frac{d{{u}_{1}}}{ds}-k{{u}_{2}} \\ {{A}_{2}}=k{{u}_{1}}+\frac{d{{u}_{2}}}{ds} \\ \end{matrix} \right. {A1=1+dsdu1−ku2A2=ku1+dsdu2
称为平面曲线的Cesaro不动点条件,即在活动标架 { R ⃗ P : α ⃗ , β ⃗ } \{{{{\vec{R}}}_{P}}:\vec{\alpha },\vec{\beta }\} {RP:α,β}所描述的点在某一瞬时的固定平面上保持绝对静止的条件。反应了活动标架 { R ⃗ P : α ⃗ , β ⃗ } \{{{{\vec{R}}}_{P}}:\vec{\alpha },\vec{\beta }\} {RP:α,β}本身的运动与所描述点 P ∗ P* P∗相对活动标架运动的关系。
平面固定坐标系
{
O
:
i
⃗
,
j
⃗
}
\{O:\vec{i},\vec{j}\}
{O:i,j}中,在曲线
Γ
P
{{\Gamma }_{P}}
ΓP外一点
P
∗
P*
P∗伴随着
Γ
P
{{\Gamma }_{P}}
ΓP上点
P
P
P运动的同时,过点
P
∗
P*
P∗的 一条直线L也伴随着
Γ
P
{{\Gamma }_{P}}
ΓP上点
P
P
P运动,形成另一过平面曲线
Γ
P
∗
{{\Gamma }_{P}}*
ΓP∗上点的直线族
Γ
l
∗
{{\Gamma }_{l}}*
Γl∗,称曲线
Γ
P
{{\Gamma }_{P}}
ΓP为原曲线,
Γ
l
∗
{{\Gamma }_{l}}*
Γl∗为
Γ
P
{{\Gamma }_{P}}
ΓP的相伴直线族。

在原曲线
Γ
P
{{\Gamma }_{P}}
ΓP上建立Frenet标架
{
R
⃗
P
:
α
⃗
,
β
⃗
}
\{{{{\vec{R}}}_{P}}:\vec{\alpha },\vec{\beta }\}
{RP:α,β},则相伴直线族
Γ
l
∗
{{\Gamma }_{l}}*
Γl∗的矢量方程为:
Γ
l
∗
:
R
⃗
l
∗
=
R
⃗
P
+
u
1
α
⃗
+
u
2
β
⃗
+
λ
(
l
1
α
⃗
+
l
2
β
⃗
)
,
l
1
2
+
l
2
2
=
1
{{\Gamma }_{l}}*:{{{\vec{R}}}_{l}}*={{{\vec{R}}}_{P}}+{{u}_{1}}\vec{\alpha }+{{u}_{2}}\vec{\beta }+\lambda ({{l}_{1}}\vec{\alpha }+{{l}_{2}}\vec{\beta }),{{l}_{1}}^{2}+{{l}_{2}}^{2}=1
Γl∗:Rl∗=RP+u1α+u2β+λ(l1α+l2β),l12+l22=1
其中:
λ
\lambda
λ为直线L的参数,而
l
⃗
{\vec{l}}
l为直线的单位方向矢量,是原曲线
Γ
P
{{\Gamma }_{P}}
ΓP弧长
s
s
s的函数。依据Frenet标架的微分运算公式,对上式求导,可得:
{
d
R
⃗
l
∗
d
s
=
A
1
α
⃗
+
A
2
β
⃗
+
λ
(
B
1
α
⃗
+
B
2
β
⃗
)
A
1
=
1
+
d
u
1
d
s
−
k
u
2
,
A
2
=
k
u
1
+
d
u
2
d
s
B
1
=
d
l
1
d
s
−
k
l
2
,
B
2
=
k
l
1
+
d
l
2
d
s
\left\{ \begin{matrix} \frac{d{{{\vec{R}}}_{l}}*}{ds}={{A}_{1}}\vec{\alpha }+{{A}_{2}}\vec{\beta }+\lambda ({{B}_{1}}\vec{\alpha }+{{B}_{2}}\vec{\beta }) \\ {{A}_{1}}=1+\frac{d{{u}_{1}}}{ds}-k{{u}_{2}},{{A}_{2}}=k{{u}_{1}}+\frac{d{{u}_{2}}}{ds} \\ {{B}_{1}}=\frac{d{{l}_{1}}}{ds}-k{{l}_{2}},{{B}_{2}}=k{{l}_{1}}+\frac{d{{l}_{2}}}{ds} \\ \end{matrix} \right.
⎩
⎨
⎧dsdRl∗=A1α+A2β+λ(B1α+B2β)A1=1+dsdu1−ku2,A2=ku1+dsdu2B1=dsdl1−kl2,B2=kl1+dsdl2
- 若直线
L
L
L为固定坐标系
{
O
:
i
⃗
,
j
⃗
}
\{O:\vec{i},\vec{j}\}
{O:i,j}中的一条固定直线,直线上每一点都固定且不随圆曲线弧长
s
s
s的变化而变化,称该直线为
绝对不动直线:
{ A 1 = 1 + d u 1 d s − k u 2 = 0 , A 2 = k u 1 − k u 2 = 0 B 1 = d l 1 d s − k l 2 = 0 , B 2 = k l 1 + d l 2 d s = 0 \left\{ \begin{matrix} {{A}_{1}}=1+\frac{d{{u}_{1}}}{ds}-k{{u}_{2}}=0,{{A}_{2}}=k{{u}_{1}}-k{{u}_{2}}=0 \\ {{B}_{1}}=\frac{d{{l}_{1}}}{ds}-k{{l}_{2}}=0,{{B}_{2}}=k{{l}_{1}}+\frac{d{{l}_{2}}}{ds}=0 \\ \end{matrix} \right. {A1=1+dsdu1−ku2=0,A2=ku1−ku2=0B1=dsdl1−kl2=0,B2=kl1+dsdl2=0 - 若直线
L
L
L为固定坐标系
{
O
:
i
⃗
,
j
⃗
}
\{O:\vec{i},\vec{j}\}
{O:i,j}中的一条固定直线,但直线上每点可沿该直线方向滑动,称该直线为
准不动直线:
d l ⃗ d s = 0 , d R ⃗ p ∗ d s × l ⃗ = 0 ⇒ B 1 = 0 , B 2 = 0 , l 1 A 2 = l 2 A 1 \frac{d\vec{l}}{ds}=0,\frac{d{{{\vec{R}}}_{p}}*}{ds}\times \vec{l}=0\Rightarrow {{B}_{1}}=0,{{B}_{2}}=0,{{l}_{1}}{{A}_{2}}={{l}_{2}}{{A}_{1}} dsdl=0,dsdRp∗×l=0⇒B1=0,B2=0,l1A2=l2A1
例1.4: 平面机构连杆曲线的相伴表示
连杆平面上任意点 P P P的运动可看做连杆上铰链点 B B B的相伴运动,相伴运动仅为(连杆)相对(连架杆)转动——即连杆平面上极坐标为 ( r p , θ p ) ({{r}_{p}},{{\theta }_{p}}) (rp,θp)的连杆点 P P P的轨迹曲线 Γ p {{\Gamma }_{p}} Γp是以 Γ B {{\Gamma }_{B}} ΓB为原曲线的相伴曲线,其方程为:
R ⃗ p = R ⃗ B + u 1 α ⃗ + u 2 β ⃗ = u 1 α ⃗ + ( u 2 − a 1 ) β ⃗ {{{\vec{R}}}_{p}}={{{\vec{R}}}_{B}}+{{u}_{1}}\vec{\alpha }+{{u}_{2}}\vec{\beta }={{u}_{1}}\vec{\alpha }+({{u}_{2}}-{{a}_{1}})\vec{\beta } Rp=RB+u1α+u2β=u1α+(u2−a1)β
其中: { u 1 = r p sin ( θ p − φ + γ ) u 2 = − r p cos ( θ p − φ + γ ) \left\{ \begin{matrix} {{u}_{1}}={{r}_{p}}\sin ({{\theta }_{p}}-\varphi +\gamma ) \\ {{u}_{2}}=-{{r}_{p}}\cos ({{\theta }_{p}}-\varphi +\gamma ) \\ \end{matrix} \right. {u1=rpsin(θp−φ+γ)u2=−rpcos(θp−φ+γ)(角度逆时针为正)








 本文介绍平面运动微分几何学的基本概念与方法,包括圆矢量函数表示曲线、Frenet标架以及相伴方法等内容。
本文介绍平面运动微分几何学的基本概念与方法,包括圆矢量函数表示曲线、Frenet标架以及相伴方法等内容。






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










