文章目录
1.1 单目相机的三维姿态解算
首先我们得知道:什么是单目相机的三维姿态解算
单目相机的三维姿态解算是指在计算机视觉领域中,使用单个摄像机来确定一个物体在三维空间中的位置和姿态。这是通过分析摄像机捕捉到的图像中物体的形状和几何关系来实现的。单目相机的三维姿态解算是计算机视觉领域中的一个挑战,因为没有深度信息,因此必须使用视差、光流和其他图像处理技术来推断三维空间中物体的位置。
1. 1 相机模型
数码相机图像拍摄的过程实际上是一个光学成像的过程。相机的成像过程涉及到四个坐标系世界坐标系、相机坐标系、图像坐标系、像素坐标系以及这四个坐标系的转换。
相机模型是光学成像模型的简化,目前有线性模型和非线性模型两种。实际的成像系统是透镜成像的非线性模型。最基本的透镜成像原理如图所示:


1.2 四个坐标系
世界坐标系: 是客观三维世界的绝对坐标系,也称客观坐标系。因为数码相机安放在三维空间中,我们需要世界坐标系这个基准坐标系来描述数码相机的位置,并且用它来描述安放在此三维环境中的其它任何物体的位置,用(Xw,Yww表示其坐标值
相机坐标系(光心坐标系):以相机的光心为坐标原点,X轴和Y轴分别平行于图像坐标系的X轴和Y轴,相机的光轴为Z轴,用(Xe,Yc,Z。示其坐标值。
图像坐标系:以CCD图像平面的中心为坐标原点,又轴和Y轴分别平行于图像平面的两条垂直边,用(ac,y)表示其坐标值。图像坐标系是用物理单位(例如毫米)表示像素在图像中的位置。
像素坐标系:以CCD图像平面的左上角顶点为原点,X轴和Y轴分别平行于图像坐标系的X轴和Y轴,用(uu)表示其坐标值。数码相机采集的图像首先是形成标准电信号的形式,然后再通过模数转换变换为数字图像。每幅图像的存储形式是M X N的数组,M行N列的图像中的每一个元素的数值代表的是图像点的灰度。这样的每个元素叫像素,像素坐标系就是以像素为单位的图像坐标系
1.2.1 像素坐标系(u,v) to 图像坐标系(x,y)

最近发现自己对于公式不太敏感了这是个坏消息
像素 -> 图像坐标系
只是坐标原点位置不一致,大小不一致,设计伸缩变换以及平移变化
{ u = x d x + u 0 v = y d y + v 0 \left\{\begin{array}{l} u=\frac{x}{d x}+u_0 \\ v=\frac{y}{d y}+v_0 \end{array}\right. {u=dxx+u0v=dyy+v0
这个方程组可以理解为将 ( x , y ) (x, y) (x,y) 坐标系中的点 ( x , y ) (x, y) (x,y) 映射到另一个坐标系中的点 ( u , v ) (u, v) (u,v) ,其中 u u u 和 v v v 分别是 ( x , y ) (x, y) (x,y) 在 x x x 和 y y y 方向上的导数,再加上常数 u 0 u_0 u0 和 v 0 v_0 v0 。
[ u v 1 ] = [ 1 d x 0 u 0 0 1 d y v 0 0 0 1 ] [ x y 1 ] \left[\begin{array}{c} u \\ v \\ 1 \end{array}\right]=\left[\begin{array}{ccc} \frac{1}{d x} & 0 & u_0 \\ 0 & \frac{1}{d y} & v_0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right] uv1 = dx1000dy10u0v01 xy1
是的,上面两个公式是等价的,可以相互推导出来。事实上,第二个公式是第一个公式的齐 次坐标形式,它将二维平面上的点 ( x , y ) (x, y) (x,y) 表示为三维齐次坐标 ( x , y , 1 ) (x, y, 1) (x,y,1) ,将二维平面上的点 的坐标变换为三维坐标系中的点的坐标,同时在变换过程中保持点的齐次性。
齐次坐标就是在原有的坐标基础上加一个维度,使得坐标更好的表现旋转等操作
1.2.2 图像坐标系(x,y) to 相机坐标系(Xc,Yc,Zc)

可以看到两个三角形相似,用初中数学可知
Δ A B O c ∼ Δ o C O c Δ P B O c ∼ Δ p C O c \begin{aligned} \Delta A B O_c \sim \Delta o C O_c \\ \Delta P B O_c \sim \Delta p C O_c \end{aligned} ΔABOc∼ΔoCOcΔPBOc∼ΔpCOc
这里看出 我们从二维推导出三维需要的信息可以从 x : f = Xc : Zc ,同理就可以得到图像的深度信息
A B o C = A O c o O c = P B p C = X c x = Z c f = Y c y \frac{A B}{\mathrm{oC}}=\frac{A O_c}{o O_c}=\frac{P B}{p C}=\frac{X_c}{x}=\frac{Z_c}{f}=\frac{Y_c}{y} oCAB=oOcAOc=pCPB=xXc=fZc=yYc

下面这个公式应该是从三维扩展到二维
x = f X c Z c , y = f Y c Z c x=f \frac{X_c}{Z_c}, y=f \frac{Y_c}{Z_c} x=fZcXc,y=fZcYc
这个公式是从三维到二维,本质是从相似三角形来的
Z c [ x y 1 ] = [ f 0 0 0 0 f 0 0 0 0 1 0 ] [ X c Y c Z c 1 ] Z_c\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=\left[\begin{array}{llll} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right]\left[\begin{array}{c} X_c \\ Y_c \\ Z_c \\ 1 \end{array}\right] Zc xy1 = f000f0001000 XcYcZc1
这个是上述公式的齐次坐标表现形式,本质上是等价的
1.2.3 世界坐标系(Xw,Yw,Zw) to 相机坐标系(Xc,Yc,Zc)
物体之间的坐标系表示坐标系的旋转变换加上平移变换
世界坐标系到相机坐标系转换关系也如此

平移加旋转
- [ X w , Y w , Z w ] \left[X_w, Y_w, Z_w\right] [Xw,Yw,Zw] 是该点在世界坐标系中的坐标。
- [ X c , Y c , Z c ] \left[X_c, Y_c, Z_c\right] [Xc,Yc,Zc] 是该点在相机坐标系中的坐标。
- R R R 是一个 3 × 3 3 \times 3 3×3 的旋转矩阵,表示将世界坐标系中的向量旋转到相机坐标系中的向量所 需的旋转变换。
-
T
T
T 是一个
3
×
1
3 \times 1
3×1 的平移向量,表示将世界坐标系中的原点平移至相机坐标系中的原点所 需的平移变换。
[ X c Y c Z c ] = R [ X w Y w Z w ] + T \left[\begin{array}{l} X_c \\ Y_c \\ Z_c \end{array}\right]=R\left[\begin{array}{l} X_w \\ Y_w \\ Z_w \end{array}\right]+T XcYcZc =R XwYwZw +T
思考 : 向量相乘就能表示他的旋转吗?
答 : 向量相乘本身不能表示旋转,但是向量相乘可以用来实现旋转变换。具体来说,我们可以使用矩阵乘法来表示旋转变换。
[
X
c
Y
c
Z
c
1
]
=
[
R
T
0
→
1
]
[
X
w
Y
w
Z
w
1
]
,
R
:
3
×
3
,
T
:
3
×
1
\left[\begin{array}{c} X_c \\ Y_c \\ Z_c \\ 1 \end{array}\right]=\left[\begin{array}{cc} R & T \\ \overrightarrow{0} & 1 \end{array}\right]\left[\begin{array}{c} X_w \\ Y_w \\ Z_w \\ 1 \end{array}\right], \mathrm{R}: 3 \times 3, \mathrm{~T}: 3 \times 1
XcYcZc1
=[R0T1]
XwYwZw1
,R:3×3, T:3×1
问: 其实我有点看不懂 , 2x2的矩阵为什么和 4x1 的矩阵能够相乘? 还有那个→0是什么来的?
答: 这个矩阵由一个 3 × 3 3 \times 3 3×3 的旋转矩阵 R \mathrm{R} R 和一个 3 × 1 3 \times 1 3×1 的平移向量 T \mathrm{T} T 组成,以及一个 4 × 4 4 \times 4 4×4 的单位矩阵中的最后一个元素为 1 。其中, 0 → \overrightarrow{0} 0 表示一个 3 × 1 3 \times 1 3×1 的零向量,是为了填充齐次 变换矩阵的最后一列,使得它变成一个 4 × 4 4 \times 4 4×4 的矩阵。
当你吧这个矩阵展开的时候 ,实际上是这个样子:
[
R
T
0
→
1
]
=
[
R
11
R
12
R
13
T
1
R
21
R
22
R
23
T
2
R
31
R
32
R
33
T
3
0
0
0
1
]
\left[\begin{array}{cc} R & T \\ \overrightarrow{0} & 1 \end{array}\right]=\left[\begin{array}{cccc} R_{11} & R_{12} & R_{13} & T_1 \\ R_{21} & R_{22} & R_{23} & T_2 \\ R_{31} & R_{32} & R_{33} & T_3 \\ 0 & 0 & 0 & 1 \end{array}\right]
[R0T1]=
R11R21R310R12R22R320R13R23R330T1T2T31
.> 是不是一目了然了
1.3 小结

阿木视频省略了很多信息,要静下心来看 ,不过这也说明她的可自学性很差

好了 接下来我们硬啃, 首先我们得知道这些参数的定义 ,有些我们可以轻易看出 f 是焦距 的就不说了
1.3.1 相机的内参数 K:
K = [ a x 0 u 0 0 a y v 0 0 0 1 ] K=\left[\begin{array}{ccc} a_x & 0 & u_0 \\ 0 & a_y & v_0 \\ 0 & 0 & 1 \end{array}\right] K= ax000ay0u0v01
这个矩阵描述了相机的内部参数,包括水平和垂直方向上的焦距 a x a_x ax 和 a y a_y ay ,相机主点的像素 坐标 ( u 0 , v 0 ) \left(u_0, v_0\right) (u0,v0) ,以及一个缩放因子 1 。这个矩阵将归一化的相机坐标映射到成像平面坐标。
1.3.2 相机外参数矩阵 M
M = [ m 11 m 12 m 13 m 14 m 21 m 22 m 23 m 24 m 31 m 32 m 33 m 34 ] M=\left[\begin{array}{llll} m_{11} & m_{12} & m_{13} & m_{14} \\ m_{21} & m_{22} & m_{23} & m_{24} \\ m_{31} & m_{32} & m_{33} & m_{34} \end{array}\right] M= m11m21m31m12m22m32m13m23m33m14m24m34
这个矩阵辐述了相机的外部参数,包括旋转矩阵 R R R 和平移向量 t t t 。 这个矩阵将一个点从世界 坐标系变换到相机坐标系。
问 ·那么相机的内参数的值 和外参数的值怎么得到呢?
答 : 相机的内参数和外参数可以通过相机标定得到。相机标定是指通过拍摄一组已知的物体或者棋盘格图案,在计算机上对图像进行分析,得到相机的内参数和外参数的过程。在相机标定时,需要拍摄一组已知的场景,比如一个平面的棋盘格图案,或者一组已知的三维点。然后,通过在图像中检测出这些点的位置,可以得到相机的内参数和外参数。
首先我们来看第一个等号:
Z
c
(
u
v
1
)
=
(
1
d
x
0
u
0
0
1
d
y
v
0
0
0
1
)
(
f
0
0
0
0
f
0
0
0
0
1
0
)
(
R
t
0
T
1
)
(
X
w
Y
w
Z
w
1
)
Z_c\left(\begin{array}{l} u \\ v \\ 1 \end{array}\right)=\left(\begin{array}{ccc} \frac{1}{d x} & 0 & u_0 \\ 0 & \frac{1}{d y} & v_0 \\ 0 & 0 & 1 \end{array}\right)\left(\begin{array}{llll} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right)\left(\begin{array}{ll} R & t \\ 0^T & 1 \end{array}\right)\left(\begin{array}{l} X_w \\ Y_w \\ Z_w \\ 1 \end{array}\right)
Zc
uv1
=
dx1000dy10u0v01
f000f0001000
(R0Tt1)
XwYwZw1
1.3.3 公式总结
这个其实是上面对应那张图的 ,变换方法 ,从右边往左边看 ,世界坐标系乘以一个旋转变换的矩阵
进行刚体变换变成了一个摄像机坐标,再乘以一个透视投影坐标变成了图像坐标,对于前面熟悉的话,这个其实很好看懂的
然后进行下一步 :
他把 公式化简了

也就是说 投影透视矩阵乘以变换等于相机内置参数 K
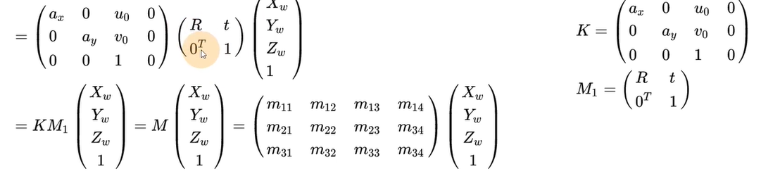
相机内置参数 乘以 旋转平移量就等于 M ,相机外置参数 ,可以看出相机外置参数包括内置参数
这就是世界坐标系变换成相机坐标系的全过程了
2 .实际成像模型:
由于相机光学系统存在加工和装配的误差,透镜就不能满足物和成像相似三角形关系

2.1 镜头的畸变模型
相机标定是通过观察已知的物体来获取相机内外参数和畸变参数的过程。一般来说,需要使用多组已知三维坐标的物体点在图像中的对应二维坐标来进行标定。通过标定得到的相机参数和畸变参数,可以用于矫正相机采集的图像。
| 参数 | 含义 | 获取方式 |
|---|---|---|
| x r , y r x_r, y_r xr,yr | 畸变前的像素坐标 | 由相机获取 |
| x i , y i x_i, y_i xi,yi | 畸变后的像素坐标 | 由相机获取 |
| σ x \sigma_x σx | 切向畸变对 x r x_r xr 的影响值 | 由 x r , y r , k 1 , k 2 x_r, y_r, k_1, k_2 xr,yr,k1,k2 计算得到 |
| σ y \sigma_y σy | 切向畸变对 y r y_r yr 的影响值 | 由 x r , y r , k 1 , k 2 x_r, y_r, k_1, k_2 xr,yr,k1,k2 计算得到 |
| k 1 k_1 k1 | 径向畸变参数 | 相机标定得到 |
| k 2 k_2 k2 | 径向畸变参数 | 相机标定得到 |
其中
m
r
(
x
r
,
y
r
)
m_r\left(x_r, y_r\right)
mr(xr,yr) 表示实际投影点的像平面坐标系下的物理坐标,
m
i
(
x
i
,
y
i
)
m_i\left(x_i, y_i\right)
mi(xi,yi) 表示理想投影点的像平 面坐标系下的物理坐标。镜头的畸变模型可表示为:
{
x
i
=
x
r
+
σ
x
y
i
=
y
r
+
σ
y
\left\{\begin{array}{l} x_i=x_r+\sigma_x \\ y_i=y_r+\sigma_y \end{array}\right.
{xi=xr+σxyi=yr+σy
σ
x
\sigma_x
σx 和
σ
y
\sigma_y
σy 是非线性畸变值,它包括径向畸变、偏心畸变和薄棱镜畸变等。
理论上来说镜头都存在径向和切向畸变,但是通常径向畸变较大,切向畸变较小。径向畸变的模型 可由下面的模型来表示:
{
σ
x
=
x
r
(
k
1
r
2
+
k
2
r
4
+
⋯
)
σ
y
=
y
r
(
k
1
r
2
+
k
2
r
4
+
⋯
)
\left\{\begin{array}{l} \sigma_x=x_r\left(k_1 r^2+k_2 r^4+\cdots\right) \\ \sigma_y=y_r\left(k_1 r^2+k_2 r^4+\cdots\right) \end{array}\right.
{σx=xr(k1r2+k2r4+⋯)σy=yr(k1r2+k2r4+⋯)
其中
k
1
,
k
2
,
k
3
,
…
k_1, k_2, k_3, \ldots
k1,k2,k3,… 表示径向畸变系数,
r
=
x
r
2
+
y
r
2
r=\sqrt{x_r^2+y_r^2}
r=xr2+yr2 ,通常情况下径向畸变系数只考虑到一阶 或二阶就可以满足精度需求了。
2.2 镜头的偏心畸变模型 :
偏心畸变模型是由于多个光学镜头的光轴不能完全共线产生的,这种畸变是由径向和切向畸变共同 构成的
具体参数如下
| 参数 | 含义 | 获取方式 |
|---|---|---|
| x r , y r x_r, y_r xr,yr | 畸变前的像素坐标 | 由相机获取 |
| x i , y i x_i, y_i xi,yi | 畸变后的像素坐标 | 由相机获取 |
| r 2 r^2 r2 | 畸变前的像素距离,即径向畸变参数 | 由 x r , y r x_r, y_r xr,yr 计算得到 |
| k 1 k_1 k1 | 径向畸变参数 | 相机标定得到 |
| k 2 k_2 k2 | 径向畸变参数 | 相机标定得到 |
| p 1 p_1 p1 | 切向畸变参数 | 相机标定得到 |
| p 2 p_2 p2 | 切向畸变参数 | 相机标定得到 |
| σ x \sigma_x σx | 切向畸变对 x r x_r xr 的影响值 | 由 x r , y r , p 1 , p 2 x_r, y_r, p_1, p_2 xr,yr,p1,p2 计算得到 |
| σ y \sigma_y σy | 切向畸变对 y r y_r yr 的影响值 | 由 x r , y r , p 1 , p 2 x_r, y_r, p_1, p_2 xr,yr,p1,p2 计算得到 |
数学模型可表示如下:
{
σ
x
=
p
1
x
r
(
3
x
r
2
+
y
r
2
)
+
2
p
2
x
r
y
r
+
o
[
(
x
r
,
y
r
)
4
]
σ
y
=
p
2
x
r
(
3
x
r
2
+
y
r
2
)
+
2
p
1
x
r
y
r
+
o
[
(
x
r
,
y
r
)
4
]
\left\{\begin{array}{l} \sigma_x=p_1 x_r\left(3 x_r^2+y_r^2\right)+2 p_2 x_r y_r+o\left[\left(x_r, y_r\right)^4\right] \\ \sigma_y=p_2 x_r\left(3 x_r^2+y_r^2\right)+2 p_1 x_r y_r+o\left[\left(x_r, y_r\right)^4\right] \end{array}\right.
⎩
⎨
⎧σx=p1xr(3xr2+yr2)+2p2xryr+o[(xr,yr)4]σy=p2xr(3xr2+yr2)+2p1xryr+o[(xr,yr)4]
其中
p
1
,
p
2
p_1, p_2
p1,p2 为切向畸变系数。薄棱镜畸变是由于镜头设计制造缺陷和加工安装所造成的,如镜头与 相机成像平面有一个很小的倾角等。因为薄棱镜畸变非常小,通常不考虑,这里只考虑径向畸变和 偏心畸变,畸变总的可以表示为:
{
x
i
=
x
r
+
x
r
(
k
1
r
2
+
k
2
r
4
)
+
p
1
x
r
(
3
x
r
2
+
y
r
2
)
+
2
p
2
x
r
y
r
y
i
=
x
r
+
y
r
(
k
1
r
2
+
k
2
r
4
)
+
p
2
x
r
(
3
x
r
2
+
y
r
2
)
+
2
p
1
x
r
y
r
\left\{\begin{array}{l} x_i=x_r+x_r\left(k_1 r^2+k_2 r^4\right)+p_1 x_r\left(3 x_r^2+y_r^2\right)+2 p_2 x_r y_r \\ y_i=x_r+y_r\left(k_1 r^2+k_2 r^4\right)+p_2 x_r\left(3 x_r^2+y_r^2\right)+2 p_1 x_r y_r \end{array}\right.
{xi=xr+xr(k1r2+k2r4)+p1xr(3xr2+yr2)+2p2xryryi=xr+yr(k1r2+k2r4)+p2xr(3xr2+yr2)+2p1xryr
补充参数含义
3. ROS的相机标定
- 不是很重要 过 !
4. 相机姿态估计:
相机姿态估计的基本思想是利用相机的内参以及已知物体在空间坐标与一一对应的图像坐标的投影 关系来求出此时物体相对于已知物体在三维空间坐标的外参,也即是旋转矩阵以及平移向量。
4.1 PnP问题
此关键算法是解决N点透视投影问题,也称作PnP (Perspective-n-Point) 问题。
N点透视投影的问题:
。N点透视投影问题是计算机图形学领域中的一个经典问题,它用于将三维场景投影到二维平面上。
在N点透视投影问题中,我们希望将一个三维场景投影到一个二维平面上,以便于显示或者处理。为了实现这个目标,我们需要确定一个投影矩阵,它可以将三维场景中的每个点映射到二维平面上的对应点。
在传统的三维计算机图形学中,通常使用四个点的透视投影矩阵来解决N点透视投影问题。这四个点通常称为“裁剪空间”,其中两个点位于近裁剪面上,两个点位于远裁剪面上。通过确定这四个点的位置,并使用透视投影矩阵,我们可以将三维场景投影到二维平面上。
对于不同的应用场景和需求,可能需要使用不同数量的点来解决N点透视投影问题。在实际应用中,通常需要通过试错和调整来确定最适合的投影矩阵和点数,以获得最佳的投影效果。
3D点
(
X
,
Y
,
Z
)
(X, Y, Z)
(X,Y,Z) 与
2
D
(
x
,
y
)
2 D(x, y)
2D(x,y) 点的联系
OpenCV提供 solvePnP 以及 solvePnPRansac 函数来求解出相机相对于已知物体的三维空间坐标 系的旋转和平移向量。
根据上式
x
=
M
⋅
[
R
∣
t
]
⋅
X
x=M \cdot[R \mid t] \cdot X
x=M⋅[R∣t]⋅X ,要求出外参数
[
R
∣
t
]
[R \mid t]
[R∣t] ,我们必须知道相机基本矩阵
M
M
M ,以及已知物体 在三维空间坐标点
X
X
X ,与之对应的图像像素坐标点
x
x
x 。

具体代码示例

4.2 旋转矩阵 :
矩阵运算显然是计算机三维坐标变换最简单方便的计算方法,因此在 opencv、opengl、工业机器 人等开发中,提到位姿旋转变换,多半用的是旋转矩阵。然而,用矩阵来表示一个旋转关系有两个 缺点:
首先,通过旋转矩阵不能直观地看出旋转的方向和角度,假设给定一个旋转矩阵,要求旋转方向不 变,旋转角度变成一半,那么新的旋转矩阵计算起来就比较麻烦了。
另一方面,旋转变换本身只有 3 个自由度,但旋转矩阵有 9 个元素,因此旋转矩阵中的元素不是相互 独立的,这在非线性优化中会带来问题。
4.2.1 绕着X轴旋转 ψ
R x ( ψ ) = [ 1 0 0 0 cos ψ − sin ψ 0 sin ψ cos ψ ] R_x(\psi)=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \psi & -\sin \psi \\ 0 & \sin \psi & \cos \psi \end{array}\right] Rx(ψ)= 1000cosψsinψ0−sinψcosψ
ψ :psi /普西/
4.2.2 绕着Y轴旋转 θ
R y ( θ ) = [ cos θ 0 sin θ 0 1 0 − sin θ 0 cos θ ] R_y(\theta)=\left[\begin{array}{ccc} \cos \theta & 0 & \sin \theta \\ 0 & 1 & 0 \\ -\sin \theta & 0 & \cos \theta \end{array}\right] Ry(θ)= cosθ0−sinθ010sinθ0cosθ
θ :theta /西塔/
4.2.3 绕着Z轴旋转
R z ( ϕ ) = [ cos ϕ − sin ϕ 0 sin ϕ cos ϕ 0 0 0 1 ] R_z(\phi)=\left[\begin{array}{ccc} \cos \phi & -\sin \phi & 0 \\ \sin \phi & \cos \phi & 0 \\ 0 & 0 & 1 \end{array}\right] Rz(ϕ)= cosϕsinϕ0−sinϕcosϕ0001
φ=Φ:phi /five/
4.3 旋转向量
旋转向量
向量旋转公式最早由 Rodrigues 提出,用一个三维向量来表示三维旋转变换,该向量的方向是旋转 轴,其模则是旋转角度。百度百科中有其详细的介绍与推导,我在这边只列一下最重要的公式。 设旋转向量的单位向量为
r
r
r ,模为
θ
\theta
θ 。三维点 (或者说三维向量)
p
p
p 在旋转向量
r
r
r 的作用下变换至
p
′
p^{\prime}
p′ , 则:
p ′ = cos θ ⋅ p + ( 1 − cos θ ) ( p ⋅ r ) r + sin θ ⋅ r × p p^{\prime}=\cos \theta \cdot p+(1-\cos \theta)(p \cdot r) r+\sin \theta \cdot r \times p p′=cosθ⋅p+(1−cosθ)(p⋅r)r+sinθ⋅r×p
| 参数 | 定义 | 获取方式 |
|---|---|---|
| p p p | 需要旋转的向量 | 通常由问题或任务确定 |
| r r r | 旋转轴的方向向量 | 通常由问题或任务确定 |
| θ \theta θ | 旋转角度 | 通常由问题或任务确定 |
| p ′ p^\prime p′ | 旋转后的向量 | 由公式计算得到 |
| cos θ \cos\theta cosθ | 旋转角度的余弦值 | cos θ = x ∣ r ∣ \cos\theta = \frac{x}{\left|{\bf r}\right|} cosθ=∣r∣x,其中 x x x是 p p p在 r {\bf r} r方向上的投影, ∣ r ∣ \left|{\bf r}\right| ∣r∣是 r {\bf r} r的模长 |
| sin θ \sin\theta sinθ | 旋转角度的正弦值 | sin θ = ∣ r × p ∣ ∣ r ∣ ∣ p ∣ \sin\theta = \frac{\left|{\bf r}\times {\bf p}\right|}{\left|{\bf r}\right|\left|{\bf p}\right|} sinθ=∣r∣∣p∣∣r×p∣,其中 r × p {\bf r}\times {\bf p} r×p是 r {\bf r} r和 p {\bf p} p的叉积 |
| ( 1 − cos θ ) ( p ⋅ r ) r (1-\cos\theta)(p\cdot r)r (1−cosθ)(p⋅r)r | 旋转轴上的投影分量 | ( 1 − cos θ ) ( p ⋅ r ) r (1-\cos\theta)(p\cdot r)r (1−cosθ)(p⋅r)r是 p p p在 r {\bf r} r方向上的投影分量 |
| sin θ ⋅ r × p \sin\theta\cdot r\times p sinθ⋅r×p | 旋转轴垂直方向上的分量 | sin θ ⋅ r × p \sin\theta\cdot r\times p sinθ⋅r×p是 r {\bf r} r和 p {\bf p} p的叉积方向上的分量 |
4.4 旋转矩阵和旋转向量相互转换:
opencv中有函数Rodrigues()用于旋转矩阵和旋转向量的转换。参照opencv文档,设旋转向量的单 位向量 r = [ r x r y r z ] T r=\left[r_x r_y r_z\right]^T r=[rxryrz]T ,旋转角度为 θ \theta θ ,对应的旋转矩阵为 R R R ,则 r r r 到 R R R 的转换是:
R = cos θ I + ( 1 − cos θ ) r r T + sin θ [ 0 − r z r y r z 0 − r x − r y r x 0 ] R=\cos \theta I+(1-\cos \theta) r r^T+\sin \theta\left[\begin{array}{ccc} 0 & -r_z & r_y \\ r_z & 0 & -r_x \\ -r_y & r_x & 0 \end{array}\right] R=cosθI+(1−cosθ)rrT+sinθ 0rz−ry−rz0rxry−rx0
其中
I
是三阶单位矩阵。反过来
R
到
r
的转换则可以利用等式:
\text { 其中 } I \text { 是三阶单位矩阵。反过来 } R \text { 到 } r \text { 的转换则可以利用等式: }
其中 I 是三阶单位矩阵。反过来 R 到 r 的转换则可以利用等式:
R
−
R
T
2
=
sin
θ
[
0
−
r
z
r
y
r
z
0
−
r
x
−
r
y
r
x
0
]
\frac{R-R^T}{2}=\sin \theta\left[\begin{array}{ccc} 0 & -r_z & r_y \\ r_z & 0 & -r_x \\ -r_y & r_x & 0 \end{array}\right]
2R−RT=sinθ
0rz−ry−rz0rxry−rx0
5. 相机三维姿态欧式角:
相机三维姿态欧式角
偏航角就是绕Yaw Axis(Z轴)旋转的角度
滚转角就是绕Rol
A
x
i
s
(
Y
\mathrm{Axis}(Y
Axis(Y 轴)旋转的角度
俯仰角就是绕Pitch Axis(X轴)旋转的角度
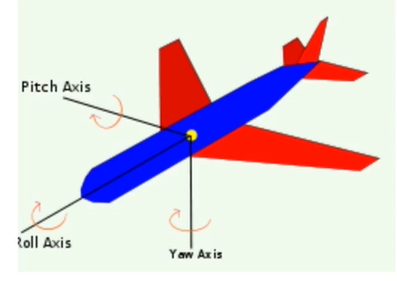

这个又是经典的阿木可学性太差的问题,不能说它没内容,就说她直接放在 谁能快速学懂她
这里我都不想琢磨她写的写的这段伪代码讲的是什么了
我们来看看另一个更加容易懂的解释
5.1 旋转矩阵 to 三维姿态角
旋转矩阵表示为:
R
=
[
R
11
R
12
R
13
R
21
R
22
R
23
R
31
R
32
R
33
]
R=\left[\begin{array}{lll} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{array}\right]
R=
R11R21R31R12R22R32R13R23R33
其中,
R
11
、
R
12
、
R
13
、
R
21
、
R
22
、
R
23
、
R
31
、
R
32
、
R
33
R_{11} 、 R_{12} 、 R_{13} 、 R_{21} 、 R_{22} 、 R_{23} 、 R_{31} 、 R_{32} 、 R_{33}
R11、R12、R13、R21、R22、R23、R31、R32、R33 均为实数。
计算物体的俯仰角 pitch, 可以通过旋转矩阵的第三行向量在
x
y
x y
xy 平面上的投影长度 计算:
cos
(
p
i
t
c
h
)
=
R
13
2
+
R
23
2
\cos (p i t c h)=\sqrt{R_{13}^2+R_{23}^2}
cos(pitch)=R132+R232
计算物体在绕
y
y
y 轴旋转的角度
y
a
w
y a w
yaw ,可以使用反正切函数
atan
2
(
y
,
x
)
\operatorname{atan} 2(y, x)
atan2(y,x) 计算:
yaw
=
atan
2
(
R
21
,
R
11
)
\text { yaw }=\operatorname{atan} 2\left(R_{21}, R_{11}\right)
yaw =atan2(R21,R11)
其中,
atan
2
(
y
,
x
)
\operatorname{atan} 2(y, x)
atan2(y,x) 函数是一个带有两个参数的反正切函数,可以处理所有四个象 限的角度值。
计算物体在绕
x
x
x 轴旋转的角度roll,可以使用反正切函数atan
2
(
y
,
x
)
2(y, x)
2(y,x) 计算:
roll
=
atan
2
(
−
R
32
,
R
33
)
\text { roll }=\operatorname{atan} 2\left(-R_{32}, R_{33}\right)
roll =atan2(−R32,R33)
其中,负号是为了得到正确的角度值。
以上三个角度值,即为物体的姿态角。
这里的atan 是 arctan的简写 即反正切函数
同时我们注意到 ,求一个角度Θ的反正切值就是求这个角度本身,公式推导如下 :
tan
−
1
(
tan
(
θ
)
)
=
tan
−
1
(
y
x
)
=
arctan
(
y
x
)
=
θ
\begin{aligned} \tan ^{-1}(\tan (\theta)) & =\tan ^{-1}\left(\frac{y}{x}\right) \\ & =\arctan \left(\frac{y}{x}\right) \\ & =\theta \end{aligned}
tan−1(tan(θ))=tan−1(xy)=arctan(xy)=θ
6. 实验环节:
rosrun camera calibration cameracalibrator.py .-size 8x6 .-square 0.024 image:=/zed/zed node/rgb/image-rectolor

可以看到标定过程

点到上面开始标定

得到一系列输出参数

根据输出更新我们这个标定的量:

更新下检测二维码的长度

代码讲解我们跳过

直接执行这段代码
python catkin_ws/src/zed-reader/zed_reader_aruco.py

可以看到检测到二维码

同时我们可以通过订阅这个话题得到消息
rostopic echo /vision_results/pose
这样的话就可以订阅到她的位置信息:
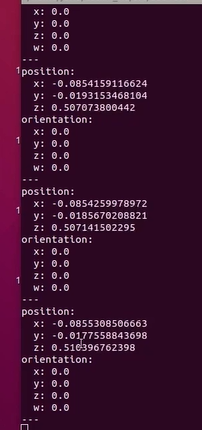
7. 参考资料 :
阿木实验室 Promethus 二次开发课程
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










