本篇博文将详细总结决策树原理,从最基本的数学公式一步步的推导。将沿着以下几个主题来总结讨论
信息熵
熵,联合熵,条件熵,互信息决策树学习算法
信息增益
ID3,C4.5,CART防止过拟合
预剪枝
随机森林决策树连续值处理和回归预测
连续值处理
回归预测
多输出的决策树回归
信息熵
熵的定义:
- 如果P表示数据样本X,那么n表示对应的标签类别数目,
表示第i类的数据样本数量占总体数据样本数量的比例。
- 如果P表示数据样本中的某一个特征,那么n表示P特征上可能的取值数目(属性值个数),
表示特征f1为某一个属性值时对应的数据样本数量占总数据样本数量比例。
熵是度量随机变量的不确定性的一个物理量,一般而言,越不确定(即概率很小,数据纯度低)熵越大,越确定(即概率很大,数据纯度高)熵越小。如果一个随机事件完全确定了,熵就是零。
条件熵:
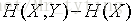
该式子定义为X发生的前提下,Y的熵:条件熵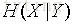
对于求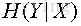
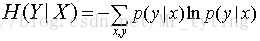
注意:上面公式推导的倒数第二步,是在X=x的前提下仅仅对y作和。(X是一个特征,里面包含多个属性值,x是X里面某一个类别)
上面推导的结果可以这样理解:
相对熵
又称互熵,交叉熵,鉴别信息,KL散度。
设p(x),q(x)是X中取值的两个概率分布,则p对q的相对熵是:
相对熵可以度量两个随机变量的“距离”
一般的,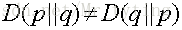
互信息
两个随机变量X,Y的互信息,定义为X,Y的联合分布和独立分布乘积的相对熵。
如果p(X),p(Y)独立,那么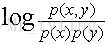
整理公式可得以下等式:
并且可得:
上面这两个不等式说明,在给定Y的情况下,X的不确定性肯定不会增大(熵不会增大),可能会减小。如果Y和X完全独立,那么等号成立,只要X和Y有一点点相关性,不确定性都会减小。
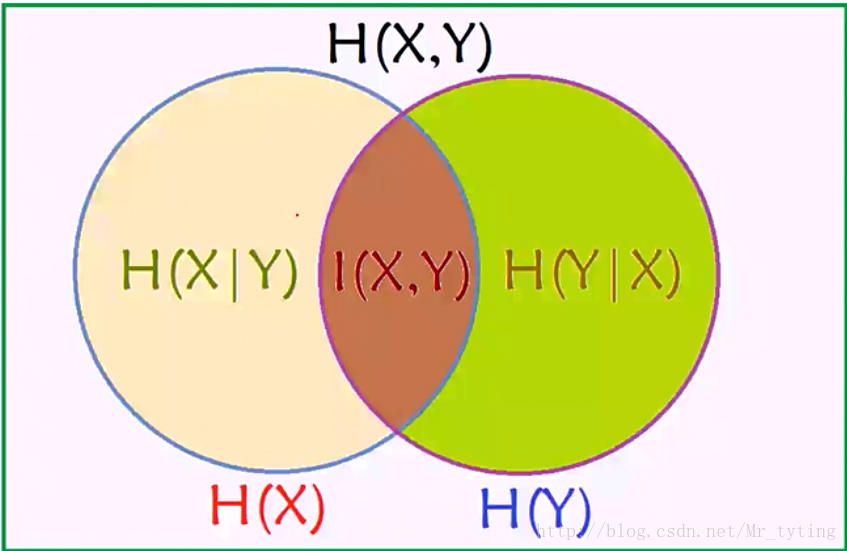
Venn图形象说明这些各种熵的关系:
注:H(X,Y):表示H(X),H(Y)的并集
决策树学习算法
所谓建立决策树,就是建立熵不断下降的一棵树。
决策树是一种树型结构,其中每个内部结点表示在一个属性上的测试,每个分支代表一 个测试输出,每个叶结点代表一种类别。
决策树学习采用的是自顶向下的递归方法, 其基本思想是以信息熵为度量构造一棵熵值下降最快的树,到叶子节点处的熵值为零, 此时每个叶节点中的实例都属于同一类。
这里我们假设有一批样本数据X,我们计算其熵值H(X),如果给定f1这个特征,那么可得熵值为H(X|f1),特征f1里面含有多个属性值f,由上面的公式可以计算出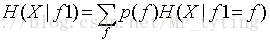
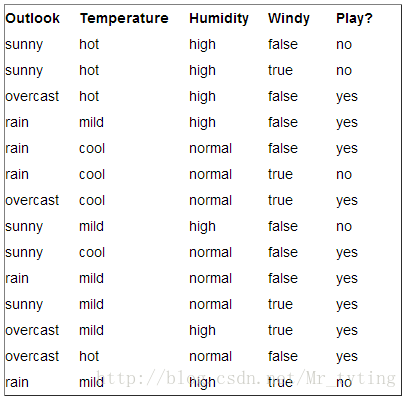
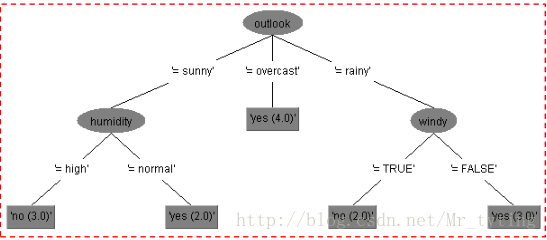
我们以这个数据集X为例来说明:
根节点信息熵为: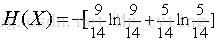
假设我们以outlook这个特征进行分类:那么上面公式中的f1即为outlook,f1里面的属性值f有sunny,rain,overcast三个,那么
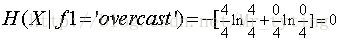


那么按照特征outlook进行分支以后得出的熵即为:
ID3
那么当我们以f1这个特征进行分类时:其信息增益为:gain(X,f1)=H(X)-H(X|f1)
那么当我们以f2这个特征进行分类时:其信息增益为:gain(X,f2)=H(X)-H(X|f2)
那么当我们以f3这个特征进行分类时:其信息增益为:gain(X,f3)=H(X)-H(X|f3)
从信息论的角度,其信息增益其实就是**互信息**I(X,f1)或I(X,f2),I(X,f3),从上面的Venn图也可看出。
我们尝试将每个特征作为分叉的特征,计算其每一个的信息增益,选择信息增益最大那个特征作为最终的分类特征。其实就是选择使熵下降最大的特征作为最终的分支特征。下一个分支特征按照上面方法递归进行。
C4.5
在上面天气的数据集X中,我们再加一列f0特征,一个索引列(1-14),那么每个索引值都不同,显然以f0特征进行分支,将会有14个分支,(注意这个f0特征是个类别型变量)那么分出来的每一个分支都是确定的,每个分支的结果不是no就是yes,那么可以确定相对与其他特征来分支,f0的熵下降肯定是最大的。此时H(X|f0)=0,从而信息增益I(X,f0)=H(X),但是这是不合理的。没有意义。那么问题出在哪里?
问题出在f0这个特征的属性值实在是太多了,属性值太多那么这个特征的熵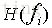
由此在C4.5中,分支的标准是信息增益率:
C4.5就是选择信息增益率最大的特征作为分支特征。
CART:基尼指数
在ID3,C4.5中,我们采用熵来衡量数据样本的不确定性(数据纯度越低),不确定性越大熵越大,不确定性越小熵越小。在这里我们用基尼值来衡量数据样本的不确定性。基尼值可以看成是熵的近似。
基尼值:
注: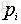
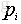
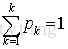
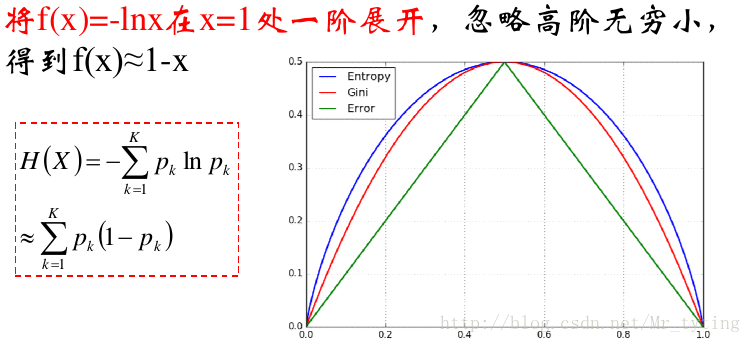
考察Gini系数的图像、熵、分类误差率三者 之间的关系
就是把这个基尼系数代替上面ID3中的熵来进行分支判断。
基尼指数:
同上面一样,在数据样本X中,特征f1的基尼指数的定义为:
CART同ID3类似,只不过这里选择使基尼指数最小的特征作为分支特征。
一个属性的信息增益(率)/gini指数越大,表明属性 对样本的熵减少的能力更强,这个属性使得数据由 不确定性变成确定性的能力越强。
防止过拟合
这里只总结两种最常用方法来防止过拟合:预剪枝,随机森林
预剪枝
首先来讲讲预剪枝,当我们对一个数据样本(或者是某一个节点,分支节点)进行划分时,首先得根据某一个标准,(如上面所说的ID3的信息增益,C4.5的信息增益率,CART的基尼指数)选出某一个特征进行划分,这里假设选出来的特征是特征F,那么是否应该进行这个划分呢?预剪枝就是要对划分前后的泛化性能进行估计。
在划分之前,对(该节点下,根节点或分支节点)数据样本进行标记,以其出现次数最多的那个类别作为所有样本的类别。然后将这个预测结果应用到验证集上,计算出验证集上精度为A1(正确分类的个数占总体个数的百分比)。
然后再以特征F进行样本划分,特征F的每一个属性值就是一个分支,每个分支的预测结果就是该分支下出现次数最多的类别。然后再应用到预测集上,计算其验证集上的精度A2。
比较划分前后的精度,如果A2>A1,那么允许以特征F对该节点进行分支,反正,禁止对该节点划分。
以上过程是一个递归的过程,在对每个节点进行划分时,不断的重复以上过程来判断是否允许进行分支。
预剪枝使得决策树的很多分支都没有“展开”,这不仅降低了过拟合的风险,还显著减少了决策树的训练时间和测试时间开销。但是另一方面,有些分支的当前划分虽然不能提高泛化能力,甚至可能导致泛化性能暂时下降,但在其基础上进行的后续划分却有可能导致性能显著提高,预剪枝基于“贪心”本质上禁止这些分支的展开,给预剪枝决策树带来欠拟合风险。
随机森林
随机森林请看我的另外一篇博文里面的总结机器学习–>集成学习–>GBDT,RandomForest
决策树连续值处理和回归预测
连续值处理
上面讨论总结的都是基于离散特征来生成决策树,那么如果有特征是连续值呢?这时候就应该对连续特征进行离散化。这正是C4.5决策树采用的算法。
上面介绍了,在离散特征中,我们以信息增益最大的特征来对数据样本进行划分,这里假定一个连续特征a,特征a有n个不同的取值,将这些值从小到大进行排序得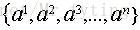
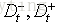
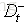
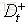
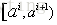
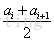
注:与离散特征不一样的是,若当前划分特征为连续特征,该连续特征依然课作为其后代节点的划分特征。
回归预测
上面都是以标签数据为离散值所做的决策树,那么当标签为连续值时,如何用决策树进行预测呢?
其实分类树和回归树的建立都是大同小异,只不过在选择分支特征的标准上不一样。在分类树中要么基于ID3,C4.5,或者基尼指数来进行划分,在回归树中我们以均方误差为标准进行分支,例如对于特征a,这里特征a不管是连续的还是离散的都可以,我们对特征a进行分支后,假设得到两个分支,就是将样本划分成两个部分A1,A2,我们分别计算A1对应标签集合的平均值作为A1部分的预测结果。A2对应的标签集合的平均值作为A2部分的预测结果。然后计算其均方误差:
连续特征的处理上面一样,只不过标准不再是最大信息增益而是最小MSE。
尝试以每个特征作为分支特征都做一次划分,然后计算其MSE,然后选择MSE最小的特征作为最终的分支特征。
显然回归树的深度越深,其叶子节点越多,那么预测结果越多样化,画出的图形越平滑。
多输出的决策树回归
我们上面说的样本个数都是形如:
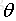
在多输出中,其Y可能是多维度的类似于:
即Y可能是k维的。
那么这个时候的均方误差MSE应该如此定义:
reg = DecisionTreeRegressor(criterion='mse', max_depth=deep)
dt = reg.fit(x, y)其回归预测的步骤和上面Y是一维的步骤大同小异。这样就可以利用决策树一次性的预测出多维度的y。在sklearn里面的随机森林已经实现这种多维度的回归预测。








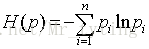
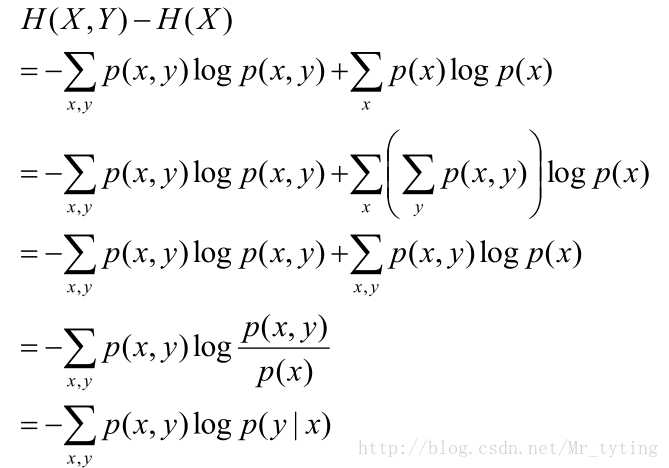
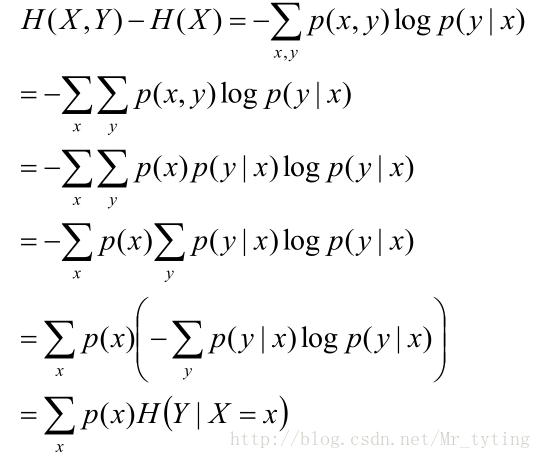
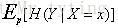
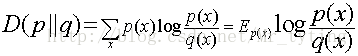
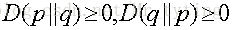
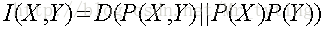
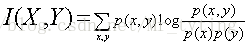
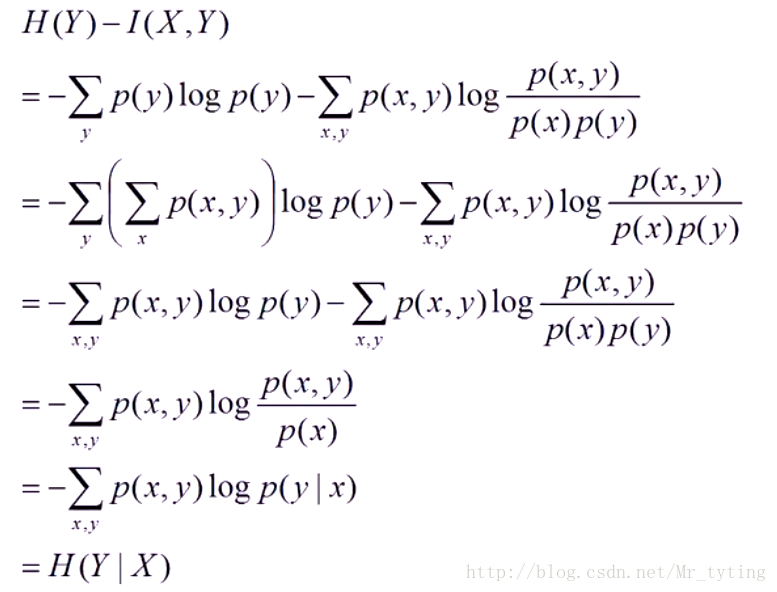
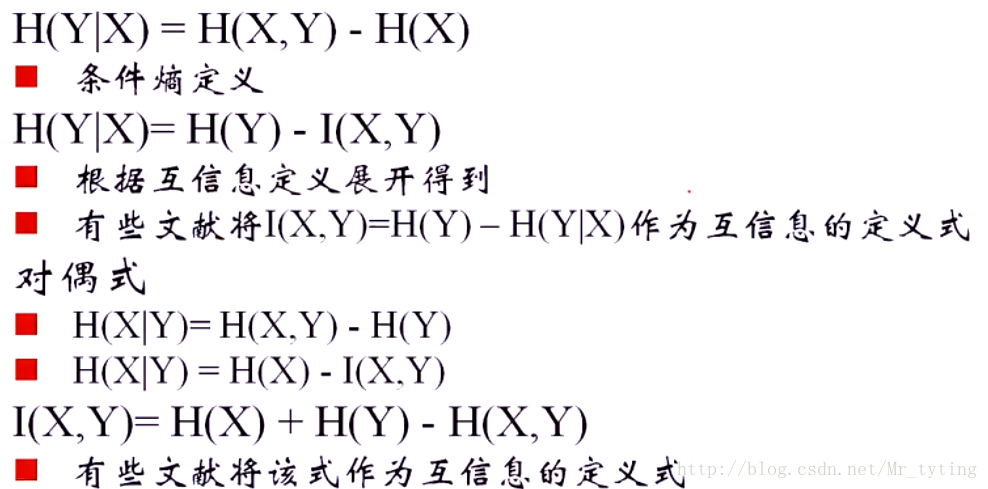

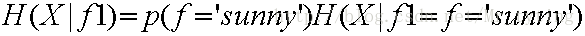
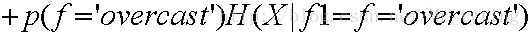
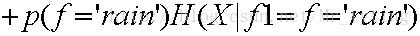
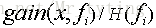
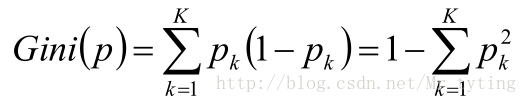
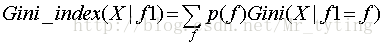
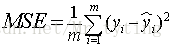
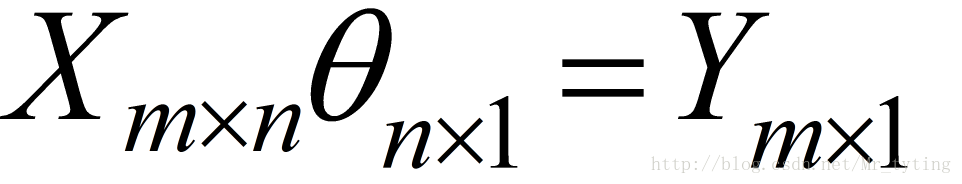
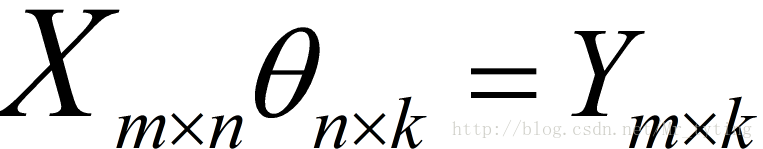
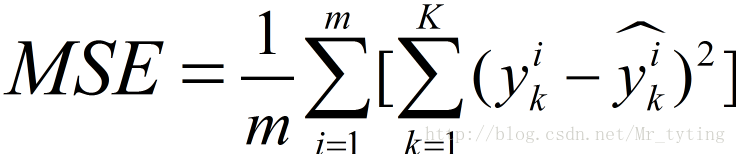














 5529
5529

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








