MulinB按:最近打算好好学习一下几种图像处理和计算机视觉中常用的 global optimization (或 energy minimization) 方法,这里总结一下学习心得。分为以下几篇:
1. Discrete Optimization: Graph Cuts and Belief Propagation
2. Quadratic Optimization: Poisson Equation and Laplacian Matrix (本篇)
3. Variational Methods for Optical Flow Estimation
2. Quadratic Optimization: Poisson Equation and Laplacian Matrix
Quadratic Optimization (Least Squares Minimization)在图像处理中的魅力要从SIGGRAPH 02和03年的两篇Gradient Domain Image Editing文章说起:Fattal的HDR Compression[1] 和Perez的Poisson Image Editing [2]。 其后,Levin的两篇文章Colorization [3]和Closed-Form Matting [4]更是将其魅力展现的淋漓尽致。而Farbman的基于Weighted Least Squares的WLS filter [5]也是在Edge-preserving Filter领域名声大噪。由于目标函数是quadratic, 这类问题的求解一般比较容易,大多都可以最终归结为求解一个大型稀疏线性方程组。而数值求解大型线性方程组是一个由来已久的问题,有着各种现成的solver,更是有着为以上这类问题量身定做的solver,见下文solver小节。
题外话:以色列的耶路撒冷希伯来大学(The Hebrew University of Jerusalem)的Lischinski教授貌似很偏爱这类方法,上面提到的这些文章大多有他的署名。
2.1 Problem I: Gradient Domain Image Editing
有心理学为证(见Poisson Image Editing [2]文章的introduction部分),对图像的gradient进行修改可以产生比较不容易感知到的artifacts,这使得很多图像编辑的工作可以放到gradient domain使得效果很逼真,比如下图的图像拼合例子(图例来自[2]):
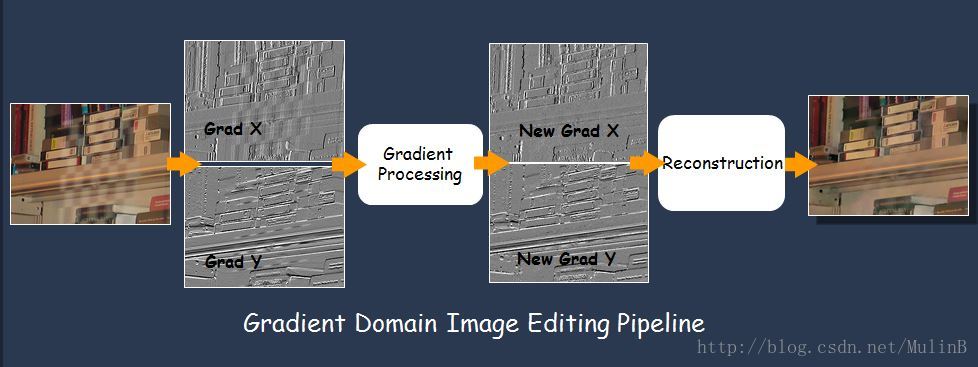
其实对gradient domain进行修改而获得逼真的编辑效果由来已久,最早见于1983年Burt-Adelson的Laplacian Pyramid [6]图像融合(这里有个简洁的中文介绍),这是题外话。在gradient domain进行图像编辑的pipeline一般如下(图例修改自ICCV 2007 Course -- Gradient Domain Manipulation Techniques,顺便赞一个,nice ppt!):
其中第一步的gradient processing根据不同的需求有具体的操作,比如HDR Compression里是将较大的gradient value进行削弱,而上面的图像拼合例子(Seamless Clone)则是将源图像的gradient拷贝到目标区域。而其中第二步中由gradient重建出新图像并非那么容易,因为经过编辑后的gradient一般是不可积分的,这时Quadratic Optimization粉墨登场。
假设待求图像为I,修改后的已知gradient是G,则通过Least Squares Minimization可以将问题formulate成如下(使得待求图像I的gradient在L2 norm下尽量接近G):
注意其中的约束条件,比如,在图像拼合例子中,非编辑区域的像素是已知的,在求解编辑区域的像素时,边界上的像素值是约束条件。上面的formulation是假设图像I是定义在x-y连续空间的函数,所以其实上述目标函数是关于I的functional(泛函,也就是“函数的函数”)。使用calculus of variation(变分法)中的Euler-Lagrange Equation (one unknown function, two variables)可以将其转化为一个非常经典的偏微分方程形式,这就是Poisson Equation:
注意其中G是已知的,I是未知的,Δ是Laplacian operator,div是divergence operator。当已知边界像素值时,该偏微分方程具有第一类边界条件(Dirichlet boundary condition),比如图像拼合;当处理整个图像时,该偏微分方程具有第二类边界条件(Neumann boundary condition),即已知边界导数值(设为0),比如HDR Compression。
上面的formulation是在x-y连续空间(像素坐标是连续的),而用于图像处理时,一般需要将其离散化(因为事实上像素坐标(x,y)是整数),上面相应的偏微分形式可以使用有限差分(finite difference)形式近似代替。具体来讲,离散化的discrete Laplacian operator如下,
而divergence operator中的一阶偏导可以用前向或者后向差分近似(由于G本身是由gradient得来,一般如果之前计算gradient使用前向差分,那么这里计算<








 本文介绍了图像处理中的全局优化技术,特别是二次优化(最小二乘法)在图像编辑中的应用,如Poisson图像编辑、颜色校正和闭合形式的羽化。通过最小化误差平方和,可以解决图像编辑中梯度域的重建问题,通常涉及求解大型稀疏线性方程组。文章还讨论了解决这些线性系统的直接法和迭代法,如Cholesky分解和共轭梯度法。
本文介绍了图像处理中的全局优化技术,特别是二次优化(最小二乘法)在图像编辑中的应用,如Poisson图像编辑、颜色校正和闭合形式的羽化。通过最小化误差平方和,可以解决图像编辑中梯度域的重建问题,通常涉及求解大型稀疏线性方程组。文章还讨论了解决这些线性系统的直接法和迭代法,如Cholesky分解和共轭梯度法。

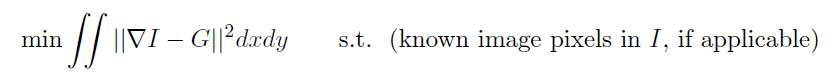
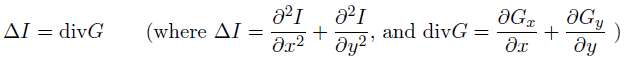
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 8811
8811

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








