线性代数学习笔记之二次型

C_TA说

已于 2024-12-20 22:48:34 修改

阅读量1.5k

点赞数 7

分类专栏： # 线性代数文章标签：线性代数学习笔记

于 2024-12-18 16:47:04 首次发布

本文链接：https://blog.csdn.net/My_Champion/article/details/144436375

版权

线性代数专栏收录该内容

7 篇文章

订阅专栏

1. 二次型的基本概念

（1）二次型的定义：含有 $n$ 个变量 $x_{1},x_{2},...x_{n}$ 的二次齐次函数，即：

$f(x_{1},x_{2},...x_{n}) = a_{11}x_{1}^{2}+...+a_{nn}x_{n}^{2}+2a_{12}x_{1}x_{2}+...+2a_{n-1,n}x_{n-1}x_{n}$ ，

称为二次型，简记 $f(x_{1},x_{2},...x_{n})$ 或 $f$ 。

备注：

①：若 $f(x_{1},x_{2},...x_{n})$ 为二次型，当包含 $n$ 个变量时，则称 $f(x_{1},x_{2},...x_{n})$ 为 $n$ 元二次型。

②：二次型可以只有平方项，也可以只有交叉项，也可以既有平方项又有交叉项。

③：此篇幅所说的对称矩阵皆为实对称矩阵。

（2）二次型的矩阵形式：

对二次型原型进行处理，可得：

$f(x_{1},x_{2},...,x_{n})=(x_{1},x_{2},...,x_{n})\begin{pmatrix} a_{11} &a_{12} &... &a_{1n} \\ a_{21} & a_{22} &... &a_{2n} \\ ...& ...& ... &... \\ a_{n1} &a_{n2} &... & a_{nn} \end{pmatrix}\begin{pmatrix} x_{1}\\ x_{2}\\ ...\\ x_{n} \end{pmatrix}$ .

简记： $f(x_{1},x_{2},...x_{n})=x^{T}Ax$ . $\Leftarrow$ 二次型的矩阵形式，其中： $x$ 是列向量，矩阵A是对称矩阵( $A^{T} = A$ )。

简要：任给一个二次型，就唯一确定一个对称矩阵；任给一个对称矩阵，就唯一确定一个二次型。

$\Rightarrow$ 二次型与对称矩阵之间存在一一对应关系。

$\Rightarrow$ 对称矩阵A就叫做二次型 $f$ 的矩阵，二次型 $f$ 就叫做对称矩阵A的二次型。

备注：

例1：已知二次型 $f(x_{1},x_{2},...x_{n})$ ，求解对称矩阵A。

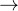
①：平方项的系数作为对称矩阵A的主对角线元素。 $kx_{i}^{2}$ $\rightarrow$ $k= a_{ii}$ 。

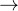
②：交叉项的系数除以2，放在变量角标的对应位置上。 $kx_{i}x_{j}$ $\rightarrow$ $\frac{k}{2}=a_{ij}$ 。

③：利用对称矩阵的对称性，进行填充其余位置。

例2：已知对称矩阵A，求解二次型 $f(x_{1},x_{2},...x_{n})$ 。

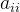
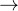
①：对称矩阵A的主对角线元素作为平方项的系数。 $a_{ii}$ $\rightarrow$ $a_{ii}x_{i}^{2}$ 。

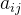
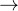
②：主对角线右上角的各元素乘以2，作为交叉项的系数。 $a_{ij}$ $\rightarrow$ $2a_{ij}x_{i}x_{j}$ 。

③：只取主对角线右上角或左下角的元素，不能上下都取。

列3：已知给定的函数 $f(x_{1},x_{2},...x_{n})=x^{T}Ax$ ，求解函数展开式形式。

①：若矩阵A不是对称矩阵，则采用对称化的方法先将矩阵A变为对称矩阵，然后再展开。

②：对称化方法：以主对角线为轴，轴线两侧相对应的元素，先做和，再除以2，得到对称矩阵。

例4：如何证明一个矩阵是二次型矩阵。

①：首先证明矩阵A是否可以写成二次型的矩阵形式 $x^{T}Ax$ 。

②：然后证明矩阵A是否是对称矩阵，即： $A^{T}=A$ 。

（3）二次型的秩：

二次型的秩就是对称矩阵A的秩，即 $r(f) = r(A)$ 。

（4）二次型的标准形的定义：若二次型中只含平方项(系数为任意实数)，不含交叉项，

即： $f(y_{1},y_{2},...y_{n}) = d_{1}y_{1}^{2}+d_{2}y_{2}^{2}+...+d_{n}y_{n}^{2}$ ，

把它称为二次型的一个标准形。

备注：

①：二次型的标准形的对称矩阵是对角矩阵，对角矩阵主对角线元素为各个平方项的系数。

②：二次型的标准形不唯一。

（5）二次型的惯性指数和符号差：

1）正惯性指数：在标准形中，正系数平方项的个数 $p$ ，称为正惯性指数。

2）负惯性指数：在标准形中，负系数平方项的个数 $q$ ，称为负惯性指数。

3）符号差：在标准形中，正惯性指数与负惯性指数的差 $p$ - $q$ ，称为符号差。

备注：

①：二次型的标准形中，二次型的秩就是非零系数平方项的个数，也是正惯性指数与负惯性指数的和 $p$ + $q$ 。

②：二次型的标准形中，二次型的矩阵A的正特征值个数与正惯性指数相等，负特征值个数与负惯性指数相等。

（6）二次型的规范形的定义：若二次型的标准形的平方项系数只能是1，-1，0这三个数，

即： $f(y_{1},y_{2},...y_{n}) = y_{1}^{2}+...+y_{p}^{2}- y_{p+1}^{2}-...-y_{p+q}^{2} +0y_{p+q+1}^{2}+...+0y_{n}^{2}$

则称为二次型的规范形。

备注：

①：在保证二次型的变量标号递增的前提下，1，-1，0这三个数出现的顺序不能变。

即： $y_{1}$ 系数为1的话， $y_{2}$ 只能是1或-1； $y_{1}$ 系数为-1的话， $y_{2}$ 系数只能是-1或0。

②：二次型的规范形的对称矩阵是对角矩阵，对角矩阵主对角线元素为1..1，-1...-1，0...。

③：二次型的规范形是唯一的。

④：根据规范形的定义可知，标准形的正负惯性指数一旦确认，那么规范形也就确定了。

2. 二次型的线性变换

（1）线性变换的定义：设有两组变量 $x_{1}$ ， $x_{2}$ ，... $x_{n}$ 和 $y_{1}$ ， $y_{2}$ ，... $y_{n}$ ，则下面的关系式：

$\left\{\begin{matrix} x_{1}=c_{11}y_{1}+c_{12}y_{2}+...+c_{1n}y_{n}\\ x_{2}=c_{21}y_{1}+c_{22}y_{2}+...+c_{2n}y_{n}\\ .........\\ x_{n}= c_{n1}y_{1}+c_{n2}y_{2}+...+c_{nn}y_{n}\\ \end{matrix}\right.$

就称为 $x_{1}$ ， $x_{2}$ ，... $x_{n}$ 到 $y_{1}$ ， $y_{2}$ ，... $y_{n}$ 的一个线性变换。

（2）线性变换的矩阵形式( $x=Cy$ )：

根据上述表达式进行整理可得：

$\begin{pmatrix} x_{1}\\ x_{2}\\ ...\\ x_{n} \end{pmatrix}=\begin{pmatrix} c_{11} & c_{12} & ...& c_{1n}\\ c_{21} & c_{22} & ...& c_{2n}\\ ...& ... & ...& ...\\ c_{n1} & c_{n2} & ...& c_{nn} \end{pmatrix}\begin{pmatrix} y_{1}\\ y_{2}\\ ...\\ y_{n} \end{pmatrix}$

简记为： $x=Cy$ 。其中矩阵C称为线性变换矩阵。

（3）线性变换重要知识点：

1）已知 $x=Cy$ 是 $x_{1}$ ， $x_{2}$ ，... $x_{n}$ 到 $y_{1}$ ， $y_{2}$ ，... $y_{n}$ 的一个线性变换，

①：若|C| ≠ 0，则称 $x=Cy$ 是可逆的线性变换，简称可逆变换。

②：若C是正交矩阵，则称 $x=Cy$ 是正交的线性变换，简称正交变换。

备注：目前涉及的线性变换至少是可逆的线性变换，即：|C| ≠ 0。

2）①： $(x=C_{1}y,y=C_{2}z)$ $\Leftrightarrow$ $x=C_{1}C_{2}z$ 。 $\leftarrow$ 这就是两次线性变换。

②： $(x=C_{1}y,y=C_{2}z)$ 都是可逆的线性变换 $\Leftrightarrow$ $x=C_{1}C_{2}z$ 是可逆的线性变换。

3）二次型经过可逆的线性变换，得到的仍是二次型，且秩不变。

证明：

①：设二次型为 $f(x_{1},x_{2},...x_{n})=x^{T}Ax$ ， $A^{T}=A$ ，可逆的线性变换为 $x=Cy$ ， $C$ 可逆。

②：由 $f(x_{1},x_{2},...x_{n})=x^{T}Ax$ ， $x=Cy$ 可得： $f(x_{1},x_{2},...x_{n})=x^{T}Ax=(Cy)^{T}ACy=y^{T}C^{T}ACy$ 。

③：另 $C^{T}AC = B$ ，则有 $f(x_{1},x_{2},...x_{n})=x^{T}Ax=y^{T}By$ 。 $\leftarrow$ 说明矩阵B满足二次型的矩阵形式。

④：对 $C^{T}AC = B$ 转置，又知 $A^{T}=A$ ，则有 $B^{T}=(C^{T}AC)^{T} =C^{T}A^{T}C=C^{T}AC=B$ 。 $\leftarrow$ 说明 $B^{T}=B$ 。

$\Rightarrow$ 二次型经过可逆的线性变换，得到的仍是二次型。

⑤： $r(B)=r(C^{T}AC)=r(A)$ 。 $\Leftarrow$ 存在可逆矩阵 $P,Q$ ，使得 $PAQ=B$ ，则 $r(A)=r(B)$ 。

$\Rightarrow$ 秩不变。

3. 矩阵的合同

（1）定义：

设矩阵A和矩阵B为 $n$ 阶矩阵，如果存在可逆矩阵C，使得 $C^{T}AC=B$ ，则称矩阵A和矩阵B是合同的，记作A $\simeq$ B。

（2）性质：

1）反身性：A $\simeq$ A. $\Leftarrow E^{T}AE =A$ .

2）交换性：A $\simeq$ B $\Leftrightarrow$ B $\simeq$ A.

3）传递性：A $\simeq$ B，B $\simeq$ C $\Leftrightarrow$ A $\simeq$ C.

4）若A $\simeq$ B，则r(A) = r(B)，A $\cong$ B.

5）若A $\simeq$ B，则 $A$ = $A^{T}$ $\Leftrightarrow$ $B$ = $B^{T}$ .

6）若A $\simeq$ B，则A与B的可逆性相同，若A，B都可逆时，则 $A^{-1}$ $\simeq$ $B^{-1}$ .

7）若A $\simeq$ B，则 $A^{T}$ $\simeq$ $B^{T}$ .

小贴士：

①：矩阵等价：矩阵A，B是同型矩阵，存在可逆矩阵P,Q，使得 $PAQ=B$ 。

②：矩阵相似：矩阵A，B都是 $n$ 阶矩阵，存在可逆矩阵P，使得 $P^{-1}AP=B$ 。

③：矩阵正交相似：矩阵A，B都是 $n$ 阶矩阵，存在正交矩阵P，使得 $P^{-1}AP=B$ 。

对于正交矩阵， $P^{-1}=P^{T}$ ，则有： $P^{T}AP=B$ 。

④：矩阵合同：矩阵A，B都是 $n$ 阶矩阵，存在可逆矩阵P，使得 $P^{T}AP=B$ 。

小贴士：二次型、线性变换、矩阵合同的关系

①：二次型 $x^{T}Ax$ ，经过可逆的线性变换 $x=Cy$ ，得到二次型 $y^{T}By$ ，其中 $B = C^{T}AC$ ，则矩阵A与矩阵B合同。

②：二次型 $x^{T}Ax$ ，经过正交的线性变换 $x=Qy$ ，得到二次型 $y^{T}By$ ，其中 $B = Q^{T}AQ= Q^{-1}AQ$ ，则矩阵A与矩阵B合同，

且正交相似。

4. 化二次型为标准形和规范形

（1）配方法：

1）针对二次型包含平方项的做法：

①：先配 $x_{1}$ ，把所有包含 $x_{1}$ 的项整合到一起，配完 $x_{1}$ 时，要将多余项反向修剪，其余项照抄。

②：再配 $x_{2}$ （配 $x_{2}$ 时不能再出现关于 $x_{1}$ 的项），按照配 $x_{1}$ 的方法，依此类推。

③：用 $y_{1}$ ， $y_{2}$ ，... $y_{n}$ 替换配好的平方项内部的式子，可得出对应的标准形。

④：先将标准形按照规范形的特性(1,-1,0)更改顺序，再用 $z_{1}$ ， $z_{2}$ ，... $z_{n}$ 替换标准形的平方项内部的式子，即可得出对应的规范形。

备注：

1. 针对上述③的替换方法可知，得出的标准形不唯一。

2. 求解③的线性变换时，要注意是 $x = Cy$ ，而不是 $y= Cx$ 。

2）针对二次型只包含交叉项的做法：

①：通过线性变换构造平方项。

②：再使用二次型包含平方项的做法求解。

备注：上述①线性变换一般取： $x_{1}=y_{1}-y_{2}$ ， $x_{2}=y_{1}+y_{2}$ ， $x_{3}=y_{3}$ ， $x_{4}=y_{4}$ ， $x_{5}=y_{5}$ ，依次类推。

（2）初等变换法：

解释说明：

①：根据（二次型经过可逆的线性变换，得到的仍是二次型）可得： $C^{T}AC=B$ 。

那么期望 $C^{T}AC=\Lambda$ ，则此时 $C,\Lambda$ 应该取何值？

②：因 $C$ 是可逆的，则有 $C=P_{1}P_{2}...P_{s}$ ，把 $C$ 带入 $C^{T}AC=\Lambda$ 可得：

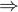
$(P_{1}P_{2}...P_{s})^{T}AP_{1}P_{2}...P_{s}=\Lambda$ $\Rightarrow$ $P_{s}^{T}...P_{2}^{T}P_{1}^{T}AP_{1}P_{2}...P_{s}=\Lambda$

③：将 $C=P_{1}P_{2}...P_{s}$ 两端同时乘以单位矩阵E可得： $EP_{1}P_{2}...P_{s}=C$

④：对比②和③结果可知：

第一步：对A和E做同样的初等列变换；

第二步：只对A做相应的初等行变换(相应就是指第一步对列做了哪个变换，第二步就对哪行做相同的变换)；

第三步：当对称矩阵A化成对角矩阵 $\Lambda$ 时，单位矩阵E化成的就是线性变换矩阵C。

备注：第一步和第二步配套使用，即列处理完，要进行相应的行处理。

⑤：获取对角矩阵 $\Lambda$ 后，继续进行④的处理，直至对角矩阵 $\Lambda$ 满足1...1，-1...-1,0...0，即可得出对应的规范形。

$eg1:\begin{pmatrix} A\\ E \end{pmatrix}=\begin{pmatrix} 1 & 1 &1 \\ 1 & 2&2 \\ 1& 2&1 \\ 1& 0&0 \\ 0 & 1 &0 \\ 0 & 0&1 \end{pmatrix} \rightarrow \begin{pmatrix} 1 & 0 &1 \\ 1 & 1&2 \\ 1& 1&1 \\ 1& -1&0 \\ 0 & 1 &0 \\ 0 & 0&1 \end{pmatrix}\rightarrow \begin{pmatrix} 1 & 0 &1 \\ 0 & 1&1 \\ 1& 1&1 \\ 1& -1&0 \\ 0 & 1 &0 \\ 0 & 0&1 \end{pmatrix}\rightarrow$ $\begin{pmatrix} 1 & 0 &0 \\ 0 & 1&1 \\ 1& 1&0 \\ 1& -1&-1 \\ 0 & 1 &0 \\ 0 & 0&1 \end{pmatrix}\rightarrow \begin{pmatrix} 1 & 0 &0 \\ 0 & 1&1 \\ 0& 1&0 \\ 1& -1&-1 \\ 0 & 1 &0 \\ 0 & 0&1 \end{pmatrix}$

$\rightarrow\begin{pmatrix} 1 & 0 &0 \\ 0 & 1&0 \\ 0& 1&-1 \\ 1& -1&0 \\ 0 & 1 &-1 \\ 0 & 0&1 \end{pmatrix}\rightarrow\begin{pmatrix} 1 & 0 &0 \\ 0 & 1&0 \\ 0& 0&-1 \\ 1& -1&0 \\ 0 & 1 &-1 \\ 0 & 0&1 \end{pmatrix}\Rightarrow \frac{\Lambda =\begin{pmatrix} 1 &0 &0 \\ 0& 1&0 \\ 0& 0 & -1 \end{pmatrix}}{C=\begin{pmatrix} 1& -1&0 \\ 0& 1& -1\\ 0& 0& 1 \end{pmatrix}}$

$eg2=\begin{pmatrix} 1& 0 &0 \\ 0 & -3&0 \\ 0 & 0 &1 \\ * & * & *\\ * &* & *\\ *& *&* \end{pmatrix}\overset{c2 * \frac{1}{\sqrt{3}}}{\rightarrow}\begin{pmatrix} 1& 0 &0 \\ 0 & \frac{-3}{\sqrt{3}}&0 \\ 0 & 0 &1 \\ * & * & *\\ * &* & *\\ *& *&* \end{pmatrix}\overset{r2 * \frac{1}{\sqrt{3}}}{\rightarrow}\begin{pmatrix} 1& 0 &0 \\ 0 &-1&0 \\ 0 & 0 &1 \\ * & * & *\\ * &* & *\\ *& *&* \end{pmatrix}\overset{c2\leftrightarrow c3}{\rightarrow}$ $\begin{pmatrix} 1& 0 &0 \\ 0 &0&-1 \\ 0 & 1 &0\\ * & * & *\\ * &* & *\\ *& *&* \end{pmatrix}\overset{r2\leftrightarrow r3}{\rightarrow}\begin{pmatrix} 1& 0 &0 \\ 0 & 1 &0\\ 0 &0&-1 \\ * & * & *\\ * &* & *\\ *& *&* \end{pmatrix}$

备注：

1. 任何二次型都可以通过可逆的线性变换化为标准形。

2. 任何二次型的矩阵都合同于对角矩阵。

（2）正交变换法：

解释说明：

因为二次型的矩阵为实对称矩阵，所以将二次型化为标准形或规范形，实际上就是将实对称矩阵正交对角化。

①：根据 $f(x_{1},x_{2},...x_{n})$ 获取实对称矩阵A。

②：采用矩阵的正交对角化方法可得：正交矩阵Q和对角矩阵Λ。

③：即求实对称矩阵A的特征值，就可得出二次型的标准形 $\lambda _{1}y_{1}^{2}+\lambda _{2}y_{2}^{2}+...+\lambda _{n}y_{n}^{2}$ 。

④：即求实对称矩阵A的特征向量并经过矩阵的正交对角化，就可得到正交变换 $x=Qy$ 。

⑤：先将标准形按照规范形的特性更改顺序，再用 $z_{1}$ ， $z_{2}$ ，... $z_{n}$ 替换标准形平方项内部式子，即可得出对应的规范形。

备注：

1. 任何二次型都可以通过正交变换化为标准形 $\lambda _{1}y_{1}^{2}+\lambda _{2}y_{2}^{2}+...+\lambda _{n}y_{n}^{2}$ ，其中 $\lambda _{1}$ , $\lambda _{2}$ ,... $\lambda _{n}$ 为 $n$ 阶实对称矩阵A的 $n$ 个特征值。

2. 若对称矩阵为实对称矩阵：二次型的矩阵A与B合同，则A与B的正特征值个数相等。 $\Leftarrow$ 惯性定理

3. 若对称矩阵为实对称矩阵：二次型的矩阵A与B合同，则A与B的正惯性指数相等。 $\Leftarrow$ 惯性定理

4. 若对称矩阵为实对称矩阵：二次型的矩阵A与B合同，则A与B具有相同的规范形。 $\Leftarrow$ 惯性定理

5. 二次型的有定性

（1）有定性的定义：设 $n$ 元二次型为 $f(x_{1},x_{2},...x_{n})=x^{T}Ax$ ( $A^{T}=A$ )，如果对于任意的非零列向量 $x$ ，

恒有 $f(x_{1},x_{2},...x_{n})=x^{T}Ax> 0$ ，则称 $f(x_{1},x_{2},...x_{n})=x^{T}Ax$ 为正定二次型。

恒有 $f(x_{1},x_{2},...x_{n})=x^{T}Ax< 0$ ，则称 $f(x_{1},x_{2},...x_{n})=x^{T}Ax$ 为负定二次型。

恒有 $f(x_{1},x_{2},...x_{n})=x^{T}Ax\geq 0$ ，则称 $f(x_{1},x_{2},...x_{n})=x^{T}Ax$ 为半正定二次型。

恒有 $f(x_{1},x_{2},...x_{n})=x^{T}Ax\leq 0$ ，则称 $f(x_{1},x_{2},...x_{n})=x^{T}Ax$ 为半负定二次型。

备注：

①：若 $n$ 元二次型 $f(x_{1},x_{2},...x_{n})=x^{T}Ax$ 的正负是确定的，则称为二次型是有定的。

②：若 $n$ 元二次型 $f(x_{1},x_{2},...x_{n})=x^{T}Ax$ 的正负不确定，则称为二次型是无定的。

（2）有定性的判别：

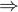
1） $n$ 元二次型的标准形 $f(x_{1},x_{2},...x_{n})=a_{1}x_{1}^{2}+a_{2}x_{2}^{2}+...+a_{n}x_{n}^{2}$ 是正定的 $\Leftrightarrow$ $a_{i}>0$ 。

证明：

①：取 $x = (1,0,0...0)$ ，若 $f$ 是正定的，则 $a_{1}> 0$ ，取 $x = (0,1,0...0)$ ，若 $f$ 是正定的，则 $a_{2}> 0$ ,

以此类推，取 $x = (0,0,0...1)$ ，若 $f$ 是正定的，则 $a_{n}> 0$ . $\Rightarrow a_{i}>0$

②：若 $a_{i}>0$ ，则 $a_{1}x_{1}^{2}+a_{2}x_{2}^{2}+...+a_{n}x_{n}^{2}\geq 0$ ，因 $x\neq 0$ ，则 $a_{1}x_{1}^{2}+a_{2}x_{2}^{2}+...+a_{n}x_{n}^{2}>0$ . $\Rightarrow$ $f$ 是正定的。

备注：若判定 $n$ 元二次型的标准形是正定的，需要保证平方项系数都是大于0的。

2）任何正定二次型经过可逆的线性变换，仍是正定二次型。

3） $n$ 元二次型 $f(x_{1},x_{2},...x_{n})=x^{T}Ax$ 是正定的

①： $\Leftrightarrow$ 它的标准形为 $d_{1}y_{1}^{2}+d_{2}y_{2}^{2}+...+d_{n}y_{n}^{2}$ ，其中 $d_{i}>0$ 。

②： $\Leftrightarrow$ 它的规范形为 $y_{1}^{2}+y_{2}^{2}+...+y_{n}^{2}$ ，其中系数全为1。

③： $\Leftrightarrow$ 它的正惯性指数为 $n$ 。

④： $\Leftrightarrow$ 对称矩阵A的所有的特征值都大于0(通过矩阵A 的正交对角化理解)。

⑤： $\Leftrightarrow$ A $\simeq$ E(通过二次型的规范形理解)。

⑥： $\Leftrightarrow$ 对称矩阵A的各阶顺序主子式全都大于0。

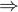
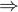
$eg:A = \begin{pmatrix} 2 & 1 & 0\\ 1& 1 & 0\\ 0& 0& 1 \end{pmatrix}\Rightarrow |2| \to \begin{vmatrix} 2 &1 \\ 1& 1 \end{vmatrix}\to\begin{vmatrix} 2 & 1 & 0\\ 1& 1 & 0\\ 0& 0& 1 \end{vmatrix}> 0$