可视化中的数学基础知识

一，坐标系

1.坐标系与坐标映射

浏览器的四个图形系统通用的坐标系分别为：

• HTML 采用的是窗口坐标系，以参考对象（参考对象通常是最接近图形元素的 position 非 static 的元素）的元素盒子左上角为坐标原点，x 轴向右，y 轴向下，坐标值对应像素值。
• SVG 采用的是视区盒子（viewBox）坐标系。这个坐标系在默认情况下，是以 svg 根元素左上角为坐标原点，x 轴向右，y 轴向下，svg 根元素右下角坐标为它的像素宽高值。如果我们设置了 viewBox 属性，那么 svg 根元素左上角为 viewBox 的前两个值，右下角为 viewBox 的后两个值。
• Canvas 采用的坐标系我们比较熟悉了，它默认以画布左上角为坐标原点，右下角坐标值为 Canvas 的画布宽高值。
• WebGL 的坐标系比较特殊，是一个三维坐标系。它默认以画布正中间为坐标原点，x 轴朝右，y 轴朝上，z 轴朝外，x 轴、y 轴在画布中范围是 -1 到 1。

共同点：但都是直角坐标系，它们都满足直角坐标系的特性：不管原点和轴的方向怎么变，用同样的方法绘制几何图形，它们的形状和相对位置都不变。

坐标转换： 正因为这四个坐标系都是直角坐标系，所以它们可以很方便地相互转化。其中，HTML、SVG 和 Canvas 都提供了 transform 的 API 能够帮助我们很方便地转换坐标系。而 WebGL 本身不提供 tranform 的 API，但我们可以在 shader 里做矩阵运算来实现坐标转换

2.Canvas实现坐标系转换

将其左上角的原点通过自带的transform和scaleAPI实现转换到画布中间，x轴为向右为正，y轴为先上为正。

这样做的目的是可以更方便、直观地计算出几个图形元素的坐标了，而不用先进行大量的计算在进行绘制。

二，向量

可视化呈现依赖于计算机图形学，而向量运算是整个计算机图形学的数学基础。

在向量运算中，除了加法表示移动点和绘制线段外，向量的点乘、叉乘运算也有特殊的意义

1.向量在图形学习中的理解

我们一般是用向量来表示一个点或者一个线段

二维向量其实就是一个包含了两个数值的数组，一个是 x 坐标值，一个是 y 坐标值。向量的维度等于“列表”的长度

一个向量包含有长度和方向信息。它的长度可以用向量的 x、y 的平方和的平方根来表示，如果用 JavaScript 来计算，就是：

v.length = function(){
    return  Math.hypot(this.x, this.y)//向量的长度，hypot() 返回欧几里德范数 sqrt(x*x + y*y)。
};  

它的方向可以用与 x 轴的夹角来表示，即：

v.dir = function() {  
    return Math.atan2(this.y, this.x);//向量的夹角
}
//在上面的代码里，Math.atan2 的取值范围是 -π到π，负数表示在 x 轴下方，正数表示在 x 轴上方。

最后，根据长度和方向的定义，我们还能推导出一组关系式：

v.x = v.length * Math.cos(v.dir);  x等于向量的长度*cos(向量的夹角)
v.y = v.length *  Math.sin(v.dir); y等于向量的长度*sin(向量的夹角)
//知道方向和长度就能求出向量的值（x,y）

这个推论意味着一个重要的事实：我们可以很简单地构造出一个绘图向量。也就是说，如果我们希望以点 (x0, y0) 为起点，沿着某个方向画一段长度为 length 的线段，我们只需要构造出如下的一个向量就可以了。

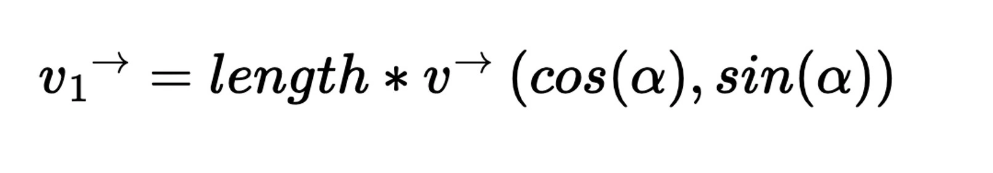
这里的α是与 x 轴的夹角，v 是一个单位向量（基向量），它的长度为 1。然后我们把向量 (x0, y0) 与这个向量 v1相加，得到的就是这条线段的终点。

2.向量加法

可以看成是在空间中的平移平行

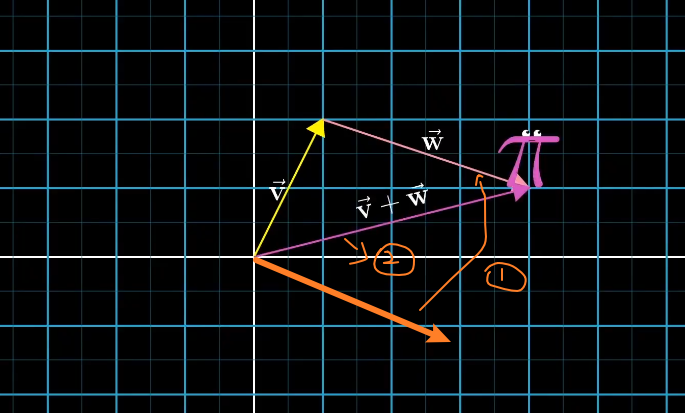
也可以看出数轴上加法的一种扩展（运算上）

3.向量数乘

• 可以看成，向量长度的数乘（倍数），这种拉伸和压缩，有时还会改变向量方式（正负）的现象，也叫向量的缩放scaling

• 倍数，也称为标量scalars

• 数字在向量中的主要作用就是缩放变量

4.向量点乘

[1]数学计算上的理解

//两个 N 维向量 a 和 b，a = [a1, a2, ...an]，b = [b1, b2, ...bn]
a•b = a1*b1 + a2*b2 + ... + an*bn

两种特殊情况：

• 第一种是，当 a、b 两个向量平行时，它们的夹角就是 0°，那么 a·b=|a|*|b|，用 JavaScript 代码表示就是：

  a.x * b.x + a.y * b.y === a.length * b.length；
  

• 第二种是，当 a、b 两个向量垂直时，它们的夹角就是 90°，那么 a·b=0，用 JavaScript 代码表示就是：

  a.x * b.x + a.y * b.y === 0;
  

[2]几何理解

投影为垂直投影

• 当向量w和向量v的方向相反时，它们的点积的值为负的
• 当向量w和向量v的方向大致相同时，它们的点积为正的
• 当向量w和向量v相互垂直时，意味着一个向量在另一个向量的投影为零向量，它们的点积为零

点积与顺序无关，也就是，谁投影到谁上都是相同的

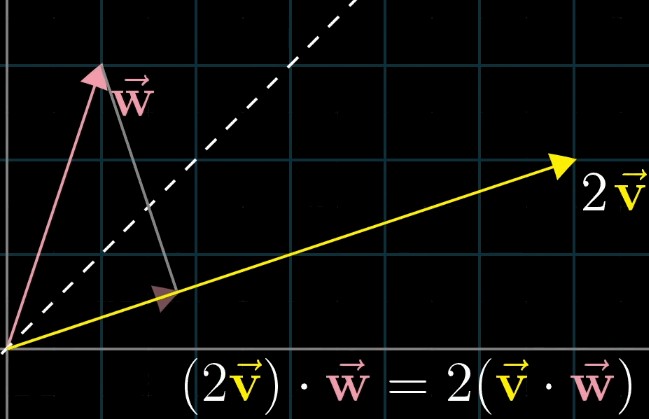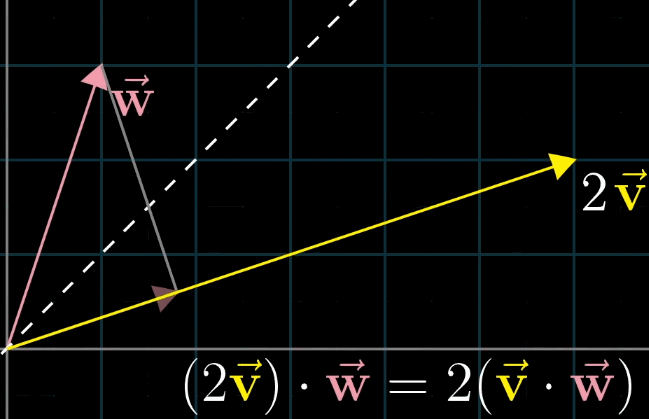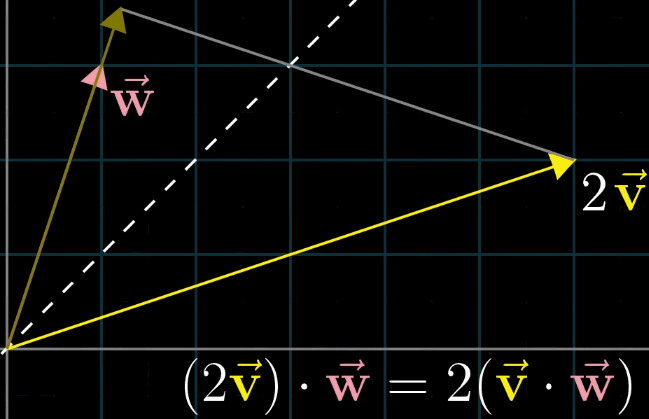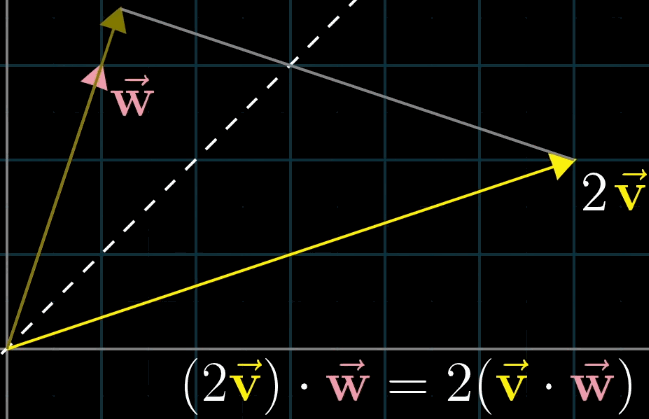
首先假设 向量v 和 向量w 长度相同，利用对称轴，两个向量互相的投影相等；

接下来如果你缩放其中一个到原来的两倍，对称性被破坏，但是缩放比例没变，最终乘法的结果也没变，一动图胜千言

我们有一个从二维空间到数轴的线性变换，它并不是由向量数值或点运算定义得到的。而是将通过空间投影到给定数轴上来定义得到的，但是因为这个变换是线性的，所以它必然 可以使用某个1x2的矩阵来描述，又因为1x2矩阵与二维向量相乘的计算过程和转置矩阵并求点积的计算过程相同，所以这个投影变换必然会与某个二维向量相关。

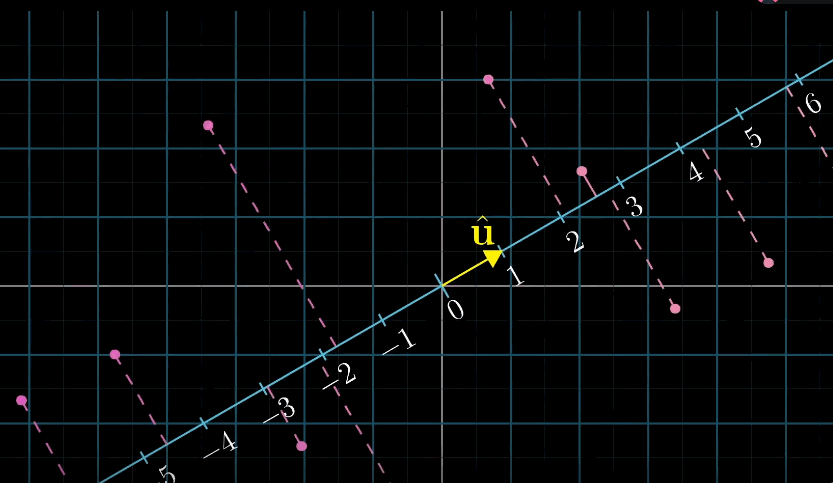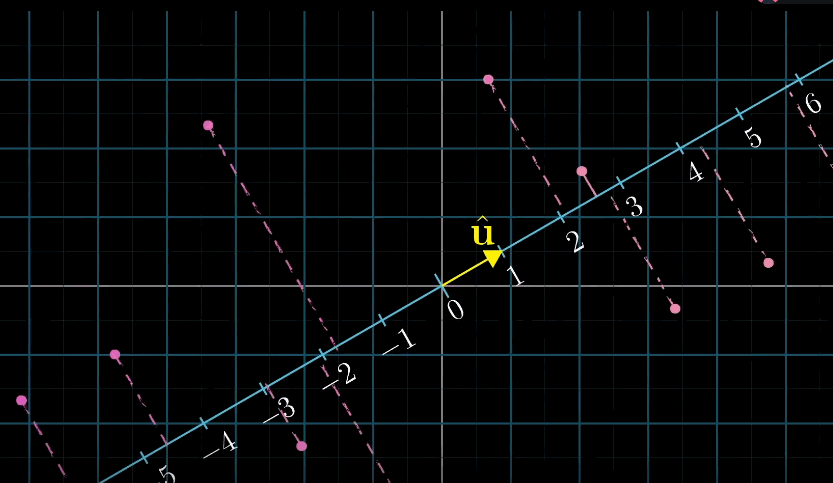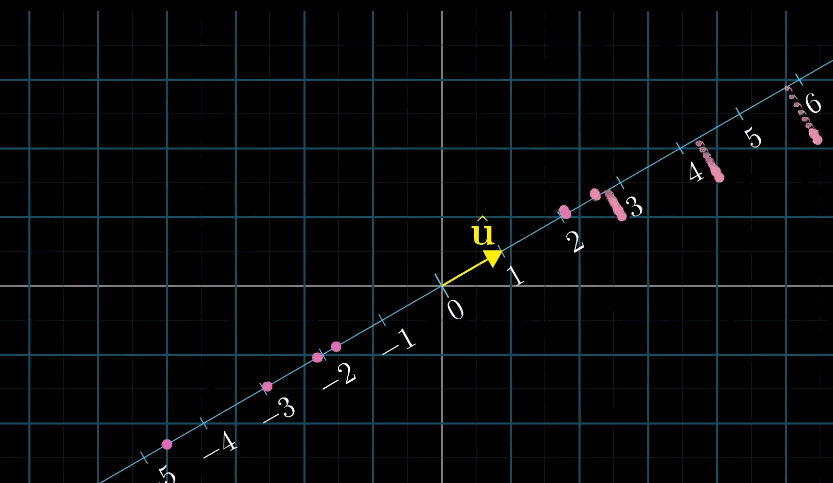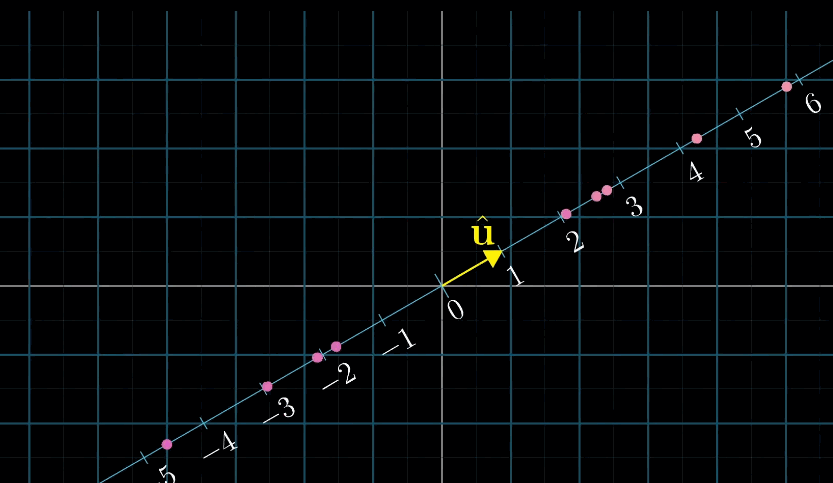
• 点积是理解投影的有力几何工具
• 方便检验两个向量的指向是否相同
• 更进一步，两个向量点乘，就是将其中一个向量转化为线性变换
• 向量仿佛是一个特定变换的概念性记号。对一般人类来说，想象空间中的向量比想象这个空间移动到数轴上更加容易

5.向量的叉乘

叉乘和点乘有两点不同：首先，向量叉乘运算的结果不是标量，而是一个向量，这个向量的长度为，叉乘向量的平行四边形的面积，这个平行四边形是向量 a 和向量 b 构成面积；

其次，两个向量的叉积与两个向量组成的坐标平面垂直

二维向量叉积的几何意义就是向量 a、b 组成的平行四边形的面积。

叉乘在数学上的计算：

假设，现在有两个三维向量 a(x1, y1, z1) 和 b(x2, y2, z2)，那么，a 与 b 的叉积可以表示为一个如下图的行列式：

//其中 i、j、k 分别是 x、y、z 轴的单位向量。我们把这个行列式展开，就能得到如下公式
a X b = [y1 * z2 - y2 * z1, - (x1 * z2 - x2 * z1), x1 * y2 - x2 * y1]

我们计算这个公式，得到的值还是一个三维向量，它的方向垂直于 a、b 所在平面。因此，我们刚才说的二维空间中，向量 a、b 的叉积方向就是垂直纸面朝向我们的。

确定叉积的方向：

右手系中向量叉乘的方向就是右手拇指的方向，那左手系中向量叉乘的方向自然就是左手拇指的方向了。

在了解了向量叉积的几何意义之后，我们通过向量叉积得到平行四边形面积，再除以底边长，就能得到点到向量所在直线的距离了

6.使用向量绘制曲线

先确定起始点和起始向量，然后通过旋转和向量加法来控制形状，就可以将曲线一段一段地绘制出来。但是它的缺点也很明显，就是数学上不太直观，需要复杂的换算才能精确确定图形的位置和大小。

Canvas2D 和 SVG 中都提供了画圆、椭圆、贝塞尔曲线的API，但是像WEBGL这种偏底层的则没有这些api了，需要自己封装。

原理：曲线是可以用折线来模拟的，当折线足够多时，折线图形便成为了曲线图形。

//绘制正边变型
function regularShape(edges = 3, x, y, step) {
  const ret = [];
  const delta = Math.PI * (1 - (edges - 2) / edges);
  let p = new Vector2D(x, y);
  const dir = new Vector2D(step, 0);
  ret.push(p);
  for(let i = 0; i < edges; i++) {
    p = p.copy().add(dir.rotate(delta));
    ret.push(p);
  }
  return ret;
}

draw(regularShape(3, 128, 128, 100));  // 绘制三角形
draw(regularShape(6, -64, 128, 50));  // 绘制六边形
draw(regularShape(11, -64, -64, 30));  // 绘制十一边形
draw(regularShape(60, 128, -64, 6));  // 绘制六十边形

三，参数方程

使用参数方程绘制曲线：通过封装函数来实现，使用参数方程能够避免向量绘制的缺点，因此是更常用的绘制方式。使用参数方程绘制曲线时，我们既可以使用有规律的曲线参数方程来绘制这些规则曲线，还可以使用二阶、三阶贝塞尔曲线来在起点和终点之间构造平滑曲线。

1.圆

圆的参数方程

图形绘制代码

const TAU_SEGMENTS = 60;
const TAU = Math.PI * 2;
function arc(x0, y0, radius, startAng = 0, endAng = Math.PI * 2) {
  const ang = Math.min(TAU, endAng - startAng);
  const ret = ang === TAU ? [] : [[x0, y0]];
  const segments = Math.round(TAU_SEGMENTS * ang / TAU);
  for(let i = 0; i <= segments; i++) {
    const x = x0 + radius * Math.cos(startAng + ang * i / segments); //方程
    const y = y0 + radius * Math.sin(startAng + ang * i / segments); //方程
    ret.push([x, y]);
  }
  return ret;
}

draw(arc(0, 0, 100));

2.椭圆

椭圆方程：

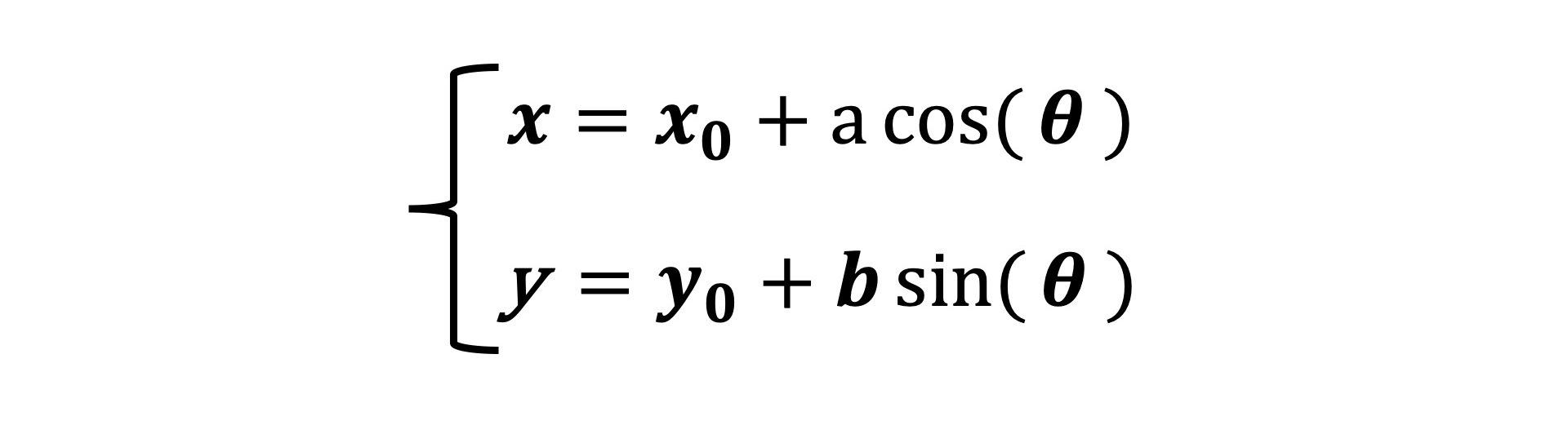
const TAU_SEGMENTS = 60;
const TAU = Math.PI * 2;
function ellipse(x0, y0, radiusX, radiusY, startAng = 0, endAng = Math.PI * 2) {
  const ang = Math.min(TAU, endAng - startAng);
  const ret = ang === TAU ? [] : [[x0, y0]];
  const segments = Math.round(TAU_SEGMENTS * ang / TAU);
  for(let i = 0; i <= segments; i++) {
    const x = x0 + radiusX * Math.cos(startAng + ang * i / segments);
    const y = y0 + radiusY * Math.sin(startAng + ang * i / segments);
    ret.push([x, y]);
  }
  return ret;
}

draw(ellipse(0, 0, 100, 50));

3.抛物线

抛物线方程：

const LINE_SEGMENTS = 60;
function parabola(x0, y0, p, min, max) {
  const ret = [];
  for(let i = 0; i <= LINE_SEGMENTS; i++) {
    const s = i / 60;
    const t = min * (1 - s) + max * s;
    const x = x0 + 2 * p * t ** 2;
    const y = y0 + 2 * p * t;
    ret.push([x, y]);
  }
  return ret;
}

draw(parabola(0, 0, 5.5, -10, 10));

4.常见曲线

如果我们为每一种曲线都分别对应实现一个函数，就会非常笨拙和繁琐。那为了方便，我们可以用函数式的编程思想，封装一个更简单的 JavaScript 参数方程绘图模块，以此来绘制出不同的曲线。这个绘图模块的使用过程主要分为三步。

第一步，我们实现一个叫做 parametric 的高阶函数，它的参数分别是 x、y 坐标和参数方程。

第二步，parametric 会返回一个函数，这个函数会接受几个参数，比如，start、end 这样表示参数方程中关键参数范围的参数，以及 seg 这样表示采样点个数的参数等等。在下面的代码中，当 seg 默认 100 时，就表示在 start、end 范围内采样 101（seg+1）个点，后续其他参数是作为常数传给参数方程的数据。

第三步，我们调用 parametric 返回的函数之后，它会返回一个对象。这个对象有两个属性：一个是 points，也就是它生成的顶点数据；另一个是 draw 方法，我们可以利用这个 draw 方法完成绘图。

// 根据点来绘制图形
function draw(points, context, {
  strokeStyle = 'black',
  fillStyle = null,
  close = false,
} = {}) {
  context.strokeStyle = strokeStyle;
  context.beginPath();
  context.moveTo(...points[0]);
  for(let i = 1; i < points.length; i++) {
    context.lineTo(...points[i]);
  }
  if(close) context.closePath();
  if(fillStyle) {
    context.fillStyle = fillStyle;
    context.fill();
  }
  context.stroke();
}

export function parametric(xFunc, yFunc) {
  return function (start, end, seg = 100, ...args) {
    const points = [];
    for(let i = 0; i <= seg; i++) {
      const p = i / seg;
      const t = start * (1 - p) + end * p;
      const x = xFunc(t, ...args); // 计算参数方程组的x
      const y = yFunc(t, ...args);  // 计算参数方程组的y
      points.push([x, y]);
    }
    return {
      draw: draw.bind(null, points),
      points,
    };
  };
}

利用绘图模块，我们就可以绘制出各种有趣的曲线了。比如，我们可以很方便地绘制出抛物线，代码如下：

// 抛物线参数方程
const para = parametric(
  t => 25 * t,
  t => 25 * t ** 2,
);

// 绘制抛物线
para(-5.5, 5.5).draw(ctx);

再比如，我们可以绘制出阿基米德螺旋线，代码如下：

const helical = parametric(
  (t, l) => l * t * Math.cos(t),
  (t, l) => l * t * Math.sin(t),
);

helical(0, 50, 500, 5).draw(ctx, {strokeStyle: 'blue'});

绘制星形线

const star = parametric(
  (t, l) => l * Math.cos(t) ** 3,
  (t, l) => l * Math.sin(t) ** 3,
);

star(0, Math.PI * 2, 50, 150).draw(ctx, {strokeStyle: 'red'});

[1]画贝塞尔曲线

前面我们说的这些曲线都比较常见，它们都是符合某种固定数学规律的曲线。但生活中还有很多不规则的图形，无法用上面这些规律的曲线去描述。那我们该如何去描述这些不规则图形呢？贝塞尔曲线（Bezier Curves）就是最常见的一种解决方式。

我们可以用 parametric 构建并绘制二阶贝塞尔曲线，代码如下所示：

const quadricBezier = parametric(
  (t, [{x: x0}, {x: x1}, {x: x2}]) => (1 - t) ** 2 * x0 + 2 * t * (1 - t) * x1 + t ** 2 * x2,
  (t, [{y: y0}, {y: y1}, {y: y2}]) => (1 - t) ** 2 * y0 + 2 * t * (1 - t) * y1 + t ** 2 * y2,
);

const p0 = new Vector2D(0, 0);
const p1 = new Vector2D(100, 0);
p1.rotate(0.75);
const p2 = new Vector2D(200, 0);
const count = 30;
for(let i = 0; i < count; i++) {
  // 绘制30条从圆心出发，旋转不同角度的二阶贝塞尔曲线
  p1.rotate(2 / count * Math.PI);
  p2.rotate(2 / count * Math.PI);
  quadricBezier(0, 1, 100, [
    p0,
    p1,
    p2,
  ]).draw(ctx);
}

在上面的代码中，我们绘制了 30 个二阶贝塞尔曲线，它们的起点都是 (0,0)，终点均匀分布在半径 200 的圆上，控制点均匀地分布在半径 100 的圆上。最终，实现的效果如下图所示

[2]贝塞尔曲线绘制Catmull–Rom

总的来说，贝塞尔曲线对于可视化，甚至整个计算机图形学都有着极其重要的意义。因为它能够针对一组确定的点，在其中构造平滑的曲线，这也让图形的实现有了更多的可能性。而且，贝塞尔曲线还可以用来构建 Catmull–Rom 曲线。Catmull–Rom 曲线也是一种常用的曲线，它可以平滑折线，我们在数据统计图表中经常会用到它。

四，多边形

在图形系统中，我们最终看到的丰富多彩的图像，都是由多边形构成的。换句话说，不论是 2D 图形还是 3D 图形，经过投影变换后，在屏幕上输出的都是多边形。

1.图形学中多边形的定义

多边形可以定义为由三条或三条以上的线段首尾连接构成的平面图形，其中，每条线段的端点就是多边形的顶点，线段就是多边形的边。

多边形又可以分为简单多边形和复杂多边形

如果一个多边形的每条边除了相邻的边以外，不和其他边相交，那它就是简单多边形，否则就是复杂多边形。

而简单多边形又分为凸多边形和凹多边形，我们主要是看简单多边形的内角来区分的。如果一个多边形中的每个内角都不超过 180°，那它就是凸多边形，否则就是凹多边形。

2.多边形的填充和边界判定

在图形系统中绘制多边形的时候，最常用的功能是填充多边形，也就是用一种颜色将多边形的内部填满。

除此之外，在可视化中用户经常要用鼠标与多边形进行交互，这就要涉及多边形的边界判定。

3.不同的图形系统如何填充多边形

不同的图形系统会用不同的方法来填充多边形。比如说，在 SVG 和 Canvas2D 中，就都内置了填充多边形的 API。在 SVG 中，我们可以直接给元素设置 fill 属性来填充，那在 Canvas2D 中，我们可以在绘图指令结束时调用 fill() 方法进行填充。

而在 WebGL 中，我们是用三角形图元来快速填充的。

[1]Canvas2D 填充多边形

Canvas2D 填充多边形可以总结为五步

第一步，构建多边形的顶点。这里我们直接构造 5 个顶点

[2]WebGL 填充多边形

在 WebGL 中，虽然没有提供自动填充多边形的方法，但是我们可以用三角形这种基本图元来快速地填充多边形。因此，在 WebGL 中填充多边形的第一步，就是将多边形分割成多个三角形。

这种将多边形分割成若干个三角形的操作，在图形学中叫做三角剖分（Triangulation）

对简单多边形尤其是凸多边形的三角剖分比较简单，而复杂多边形由于有边的相交和面积重叠区域，所以相对困难许多，因为那些算法会比较复杂涉及很多图形学的底层数学知识

这里，我们就直接利用 GitHub 上的一些成熟的库（常用的如Earcut、Tess2.js以及cdt2d），来对多边形进行三角剖分就可以了。

例如利用Earcut库来进行三角剖分

//上图的顶点数据
const vertices = [
  [-0.7, 0.5],
  [-0.4, 0.3],
  [-0.25, 0.71],
  [-0.1, 0.56],
  [-0.1, 0.13],
  [0.4, 0.21],
  [0, -0.6],
  [-0.3, -0.3],
  [-0.6, -0.3],
  [-0.45, 0.0],
];

首先，我们要对它进行三角剖分。使用 Earcut 库的操作很简单，我们直接调用它的 API 就可以完成对多边形的三角剖分，具体代码如下：

import {earcut} from '../common/lib/earcut.js';

const points = vertices.flat();
const triangles = earcut(points);

因为 Earcut 库只接受扁平化的定点数据，所以我们先用了数组的 flat 方法将顶点扁平化，然后将它传给 Earcut 进行三角剖分。这样返回的结果是一个数组，这个数组的值是顶点数据的 index，结果如下：

[1, 0, 9, 9, 8, 7, 7, 6, 5, 4, 3, 2, 2, 1, 9, 9, 7, 5, 4, 2, 9, 9, 5, 4]

这里的值，比如 1 表示 vertices 中下标为 1 的顶点，即点 (-0.4, 0.3)，每三个值可以构成一个三角形，所以 1、0、9 表示由 (-0.4, 0.3)、(-0.7, 0.5) 和 (-0.45, 0.0) 构成的三角形。

然后，我们将顶点和 index 下标数据都输入到缓冲区，通过 gl.drawElements 方法就可以把图形显示出来。具体的代码如下：

const position = new Float32Array(points);
const cells = new Uint16Array(triangles);

//将数据存到缓存区
const pointBuffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, pointBuffer);
gl.bufferData(gl.ARRAY_BUFFER, position, gl.STATIC_DRAW);

//从缓存区中读取数据
const vPosition = gl.getAttribLocation(program, 'position');
gl.vertexAttribPointer(vPosition, 2, gl.FLOAT, false, 0, 0);
gl.enableVertexAttribArray(vPosition);


const cellsBuffer = gl.createBuffer();
gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, cellsBuffer);
gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, cells, gl.STATIC_DRAW);


gl.clear(gl.COLOR_BUFFER_BIT);
gl.drawElements(gl.TRIANGLES, cells.length, gl.UNSIGNED_SHORT, 0);

被剖分为了8个三角形

实际上，WebGL 是对这个多边形三角剖分后的每个三角形分别进行填充的

上面为2D 图形的三角剖分。那针对 3D 模型，WebGL 在绘制的时候，也需要使用三角剖分，而 3D 的三角剖分又被称为网格化（Meshing）。

不过，因为 3D 模型比 2D 模型更加复杂，顶点的数量更多，所以针对复杂的 3D 模型，我们一般不在运行的时候进行三角剖分，而是通过设计工具把图形的三角剖分结果直接导出进行使用。也就是说，在 3D 渲染的时候，我们一般使用的模型数据都是已经经过三角剖分以后的顶点数据。

总的来说，无论是绘制 2D 还是 3D 图形，WebGL 都需要先把它们进行三角剖分，然后才能绘制。因此，三角剖分是 WebGL 绘图的基础。

4.不同图形系统判断点在多边形内部

Canvas和SVG图形系统都是自带有判断的api的

[1]Canvas2D判断点在多边形内部

首先，先用 Canvas2D 来绘制并填充这个多边形

然后，我们在 canvas 上添加 mousemove 事件，在事件中计算鼠标相对于 canvas 的位置，再将这个位置传给 isPointInPath 方法，isPointInPath 方法就会自动判断这个位置是否位于图形内部。代码如下：

const {left, top} = canvas.getBoundingClientRect();

canvas.addEventListener('mousemove', (evt) => {
  const {x, y} = evt;
  // 坐标转换
  const offsetX = x - left;
  const offsetY = y - top;

  ctx.clearRect(-256, -256, 512, 512);

  if(ctx.isPointInPath(offsetX, offsetY)) {
    draw(ctx, poitions, 'transparent', 'green');
  } else {
    draw(ctx, poitions, 'transparent', 'red');
  }
});

五，矩阵

在实际绘制的时候，我们经常需要在画布上绘制许多轮廓相同的图形，难道这也需要我们重复地去计算每个图形的顶点吗？当然不需要。我们只需要创建一个基本的几何轮廓，然后通过线性/非线性变换来改变几何图形的位置、形状、大小和角度。

1.线性变换

[1]几何直观理解

变换本质是“函数”的一种花哨的说法，它介绍内容，并输出对应的结果。

变换和函数又有所不同，因为使用变换是在以特定的方式来可视化这一输入——输出的关系

一种理解“向量函数”的方法是使用运动

例如一个变换接收一个向量并输出一个向量，我们可以想象这个输入向量移动到输出向量的位置

线性代数限制在一种特殊类型的变换上，称为“线性变换”，这种变换更容易理解

直观的说，如果变换具有以下两条性质，我们便可以称他说线性的

1. 直线在变换后仍然为直线，不能有所弯曲
2. 原点必须保持固定

示例：

保持网格平行且等距分布的变换

根据原点旋转

更多详见线性代数的本质文章

[2]常见的线性变换

旋转变换

几何理解：

例如将整个空间逆时针旋转90度，那么i帽便落在坐标（0，1）上，j帽落在坐标（-1，0）上，

如果想计算出任意向量在逆时针旋转90度后的位置，只需要把他和上面矩阵相乘即可

之前画树的旋转代码

class Vector2D {
  ...  
  rotate(rad) {
    const c = Math.cos(rad),
      s = Math.sin(rad);
    const [x, y] = this;

    this.x = x * c + y * -s;
    this.y = x * s + y * c;

    return this;
  }
}

假设向量 P 的长度为 r，角度是⍺，现在我们要将它逆时针旋转⍬角，此时新的向量P’的参数方程为：

然后，因为 rcos⍺、rsin⍺是向量 P 原始的坐标 x0、y0，所以，我们可以把坐标代入到上面的公式中，就会得到如下的公式：

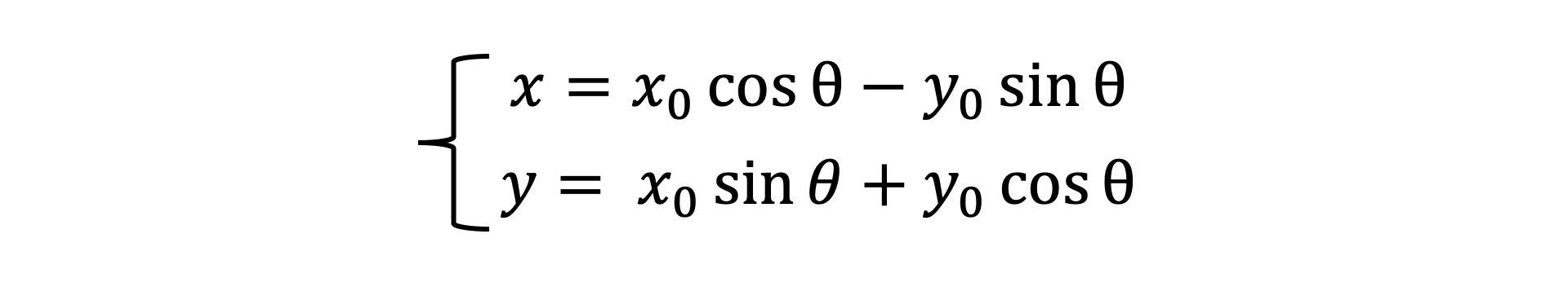
最后，我们再将它写成矩阵形式，就会得到一个旋转矩阵。（同时可以利用几何意义来理解：脑补）

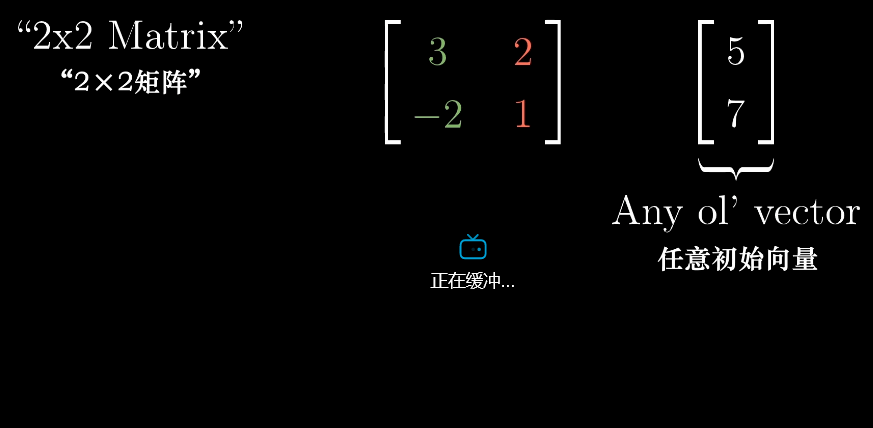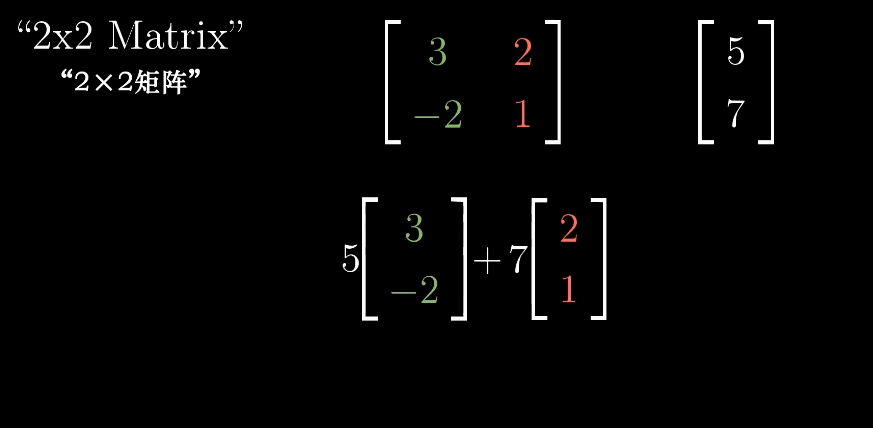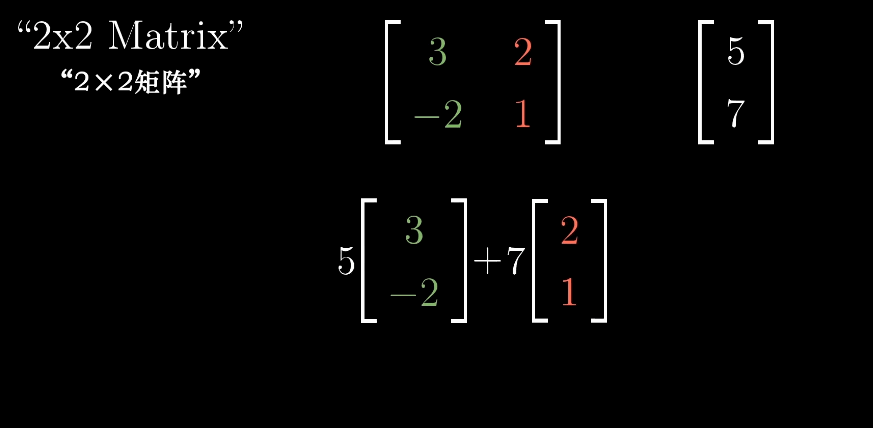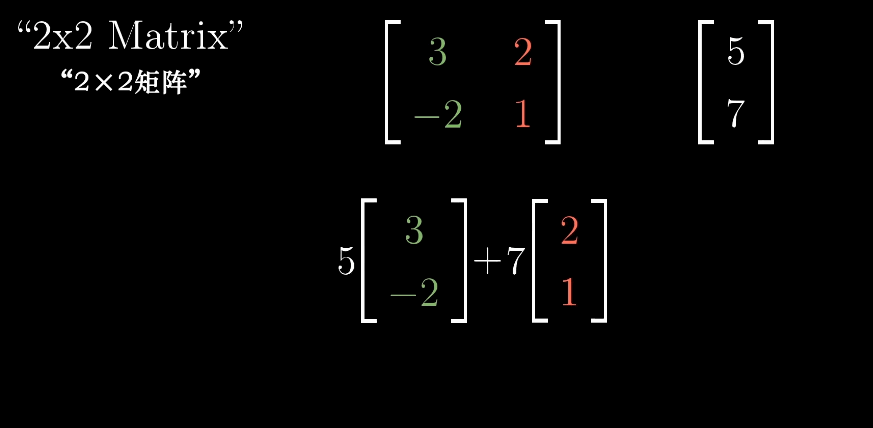
缩放变换

在几何意义中便是数乘（脑补）

缩放变换。缩放变换也很简单，我们可以直接让向量与标量（标量只有大小、没有方向）相乘。

几何理解

对于得到的这个公式，我们也可以把它写成矩阵形式。结果如下：

旋转和缩放都可以写成矩阵与向量相乘的形式。这种能写成矩阵与向量相乘形式的变换，就叫做线性变换。

线性变换除了可以满足仿射变换的 2 个性质之外，还有 2 个额外的性质：

• 线性变换不改变坐标原点（因为如果 x0、y0等于零，那么 x、y 肯定等于 0）

• 线性变换可以叠加，多个线性变换的叠加结果就是将线性变换的矩阵依次相乘，再与原始向量相乘

那根据线性变换的第 2 条性质，我们就能总结出一个通用的线性变换公式，即一个原始向量 P0经过 M1、M2、…Mn 次的线性变换之后得到最终的坐标 P。线性变化的叠加是一个非常重要的性质，它是我们对图形进行变换的基础，所以你一定要牢记线性变化的叠加性质。

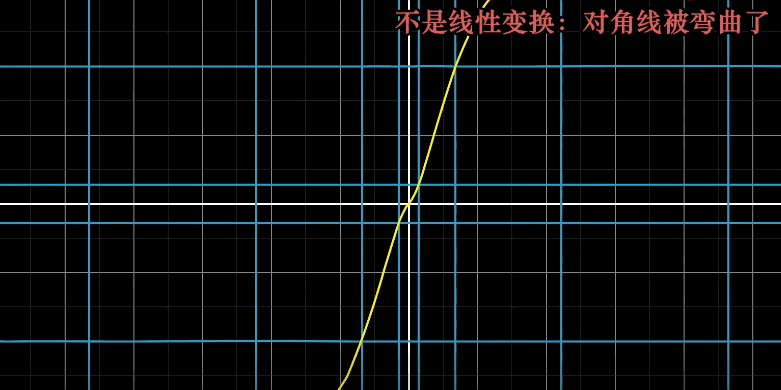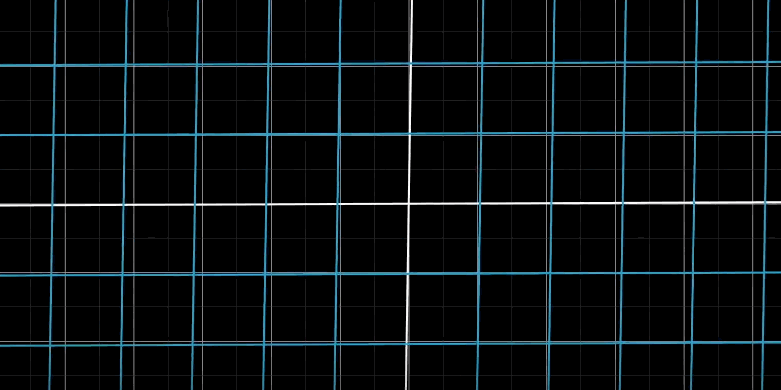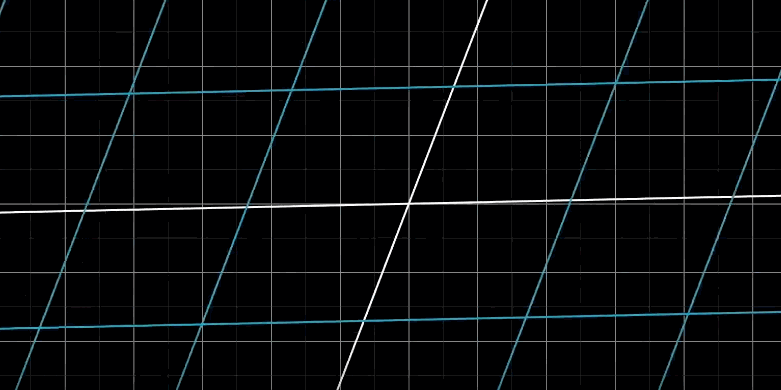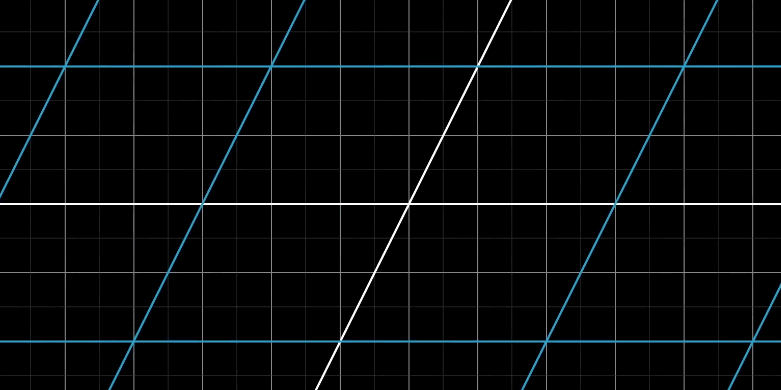
2.非线性变换

[1]几何直观理解

直线弯曲了，不是线性变换

这也不是线性变换，因为它的原点发送变化了，这也叫仿射变换

[2]仿射变换

仿射变换是拓扑学和图形学中一个非常重要的基础概念。利用它，我们才能在可视化应用中快速绘制出形态、位置、大小各异的众多几何图形，所以需要重点学习。

仿射变换简单来说就是“线性变换 + 平移”

仿射变换的性质

• 仿射变换前是直线段的，仿射变换后依然是直线段
• 对两条直线段 a 和 b 应用同样的仿射变换，变换前后线段长度比例保持不变

常见的仿射变换形式包括平移、旋转、缩放以及它们的组合。

向量的平移

其中，平移变换是最简单的仿射变换。如果我们想让向量 P(x0, y0) 沿着向量 Q(x1, y1) 平移，只要将 P 和 Q 相加就可以了。（也就是向量加法）

平移后向量p的坐标

小结

总的来说，向量的基本仿射变换分为平移、旋转与缩放，其中旋转与缩放属于线性变换，而平移不属于线性变换

基于此，我们可以得到仿射变换的一般表达式，如下图所示：

[3]仿射变换的公式优化

上面这个公式我们还可以改写成矩阵的形式，在改写的公式里，我们实际上是给线性空间增加了一个维度。换句话说，我们用高维度的线性变换表示了低维度的仿射变换！

这样，我们就将原本 n 维的坐标转换为了 n+1 维的坐标。这种 n+1 维坐标被称为齐次坐标，对应的矩阵就被称为齐次矩阵。

齐次坐标和齐次矩阵是可视化中非常常用的数学工具，它能让我们用线性变换来表示仿射变换。

这样一来，我们就能利用线性变换的叠加性质，来非常方便地进行各种复杂的仿射变换了。落实到共识上，就是把这些变换的矩阵相乘得到一个新的矩阵，再把它乘以原向量。我们在绘制几何图形的时候会经常用到它，所以你要记住这个公式。

[4]仿射变换应用举例：实现粒子动画

在粒子动画的实现过程中，我们通常需要在界面上快速改变一大批图形的大小、形状和位置，所以用图形的仿射变换来实现是一个很好的方法。

创建三角形

创建三角形一共可以分为两步，第一步，我们定义三角形的顶点并将数据送到缓冲区

const position = new Float32Array([
  -1, -1,
  0, 1,
  1, -1,
]);
//将点数据推到缓存区
const bufferId = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, bufferId);
gl.bufferData(gl.ARRAY_BUFFER, position, gl.STATIC_DRAW);
//缓存区数据读取到GPU
const vPosition = gl.getAttribLocation(program, 'position');
gl.vertexAttribPointer(vPosition, 2, gl.FLOAT, false, 0, 0);
gl.enableVertexAttribArray(vPosition);

第二步，我们实现一个创建随机三角形属性的函数。

function randomTriangles() {
  const u_color = [Math.random(), Math.random(), Math.random(), 1.0]; // 随机颜色
  const u_rotation = Math.random() * Math.PI; // 初始旋转角度
  const u_scale = Math.random() * 0.05 + 0.03; // 初始大小
  const u_time = 0;
  const u_duration = 3.0; // 持续3秒钟

  const rad = Math.random() * Math.PI * 2;
  const u_dir = [Math.cos(rad), Math.sin(rad)]; // 运动方向
  const startTime = performance.now();

  return {u_color, u_rotation, u_scale, u_time, u_duration, u_dir, startTime};
}

其中的参数包括颜色 u_color、初始旋转角度 u_rotation、初始大小 u_scale、初始时间 u_time、动画持续时间 u_diration、运动方向 u_dir 和创建时间 startTime。除了 startTime 之外的数据，我们都需要传给 shader 去处理。

设置 uniform 变量

attribute 变量是对应于顶点的。也就是说，几何图形有几个顶点就要提供几份 attribute 数据。并且，attribute 变量只能在顶点着色器中使用，如果要在片元着色器中使用，需要我们通过 varying 变量将它传给片元着色器才行

而 uniform 声明的变量不同，uniform 声明的变量和其他语言中的常量一样，我们赋给 uniform 变量的值在 shader 执行的过程中不可改变。而且一个变量的值是唯一的，不随顶点变化。uniform 变量既可以在顶点着色器中使用，也可以在片元着色器中使用。

在 WebGL 中，我们可以通过 gl.uniformXXX(loc, u_color); 的方法将数据传给 shader 的 uniform 变量。其中，XXX 是我们随着数据类型不同取得不同的名字。

gl.uniform1f 传入一个浮点数，对应的 uniform 变量的类型为 float

gl.uniform4f 传入四个浮点数，对应的 uniform 变量类型为 float[4]

gl.uniform3fv 传入一个三维向量，对应的 uniform 变量类型为 vec3

gl.uniformMatrix4fv 传入一个 4x4 的矩阵，对应的 uniform 变量类型为 mat4

接下来将随机三角形信息传给shader里的uniform变量

function setUniforms(gl, {u_color, u_rotation, u_scale, u_time, u_duration, u_dir}) {
  // gl.getUniformLocation 拿到uniform变量的指针
  let loc = gl.getUniformLocation(program, 'u_color');
  // 将数据传给 unfirom 变量的地址
  gl.uniform4fv(loc, u_color);

  loc = gl.getUniformLocation(program, 'u_rotation');
  gl.uniform1f(loc, u_rotation);

  loc = gl.getUniformLocation(program, 'u_scale');
  gl.uniform1f(loc, u_scale);

  loc = gl.getUniformLocation(program, 'u_time');
  gl.uniform1f(loc, u_time);

  loc = gl.getUniformLocation(program, 'u_duration');
  gl.uniform1f(loc, u_duration);

  loc = gl.getUniformLocation(program, 'u_dir');
  gl.uniform2fv(loc, u_dir);
}

用requestAnimationFrame实现动画

然后，我们使用 requestAnimationFrame 实现动画。具体的方法就是，我们在 update 方法中每次新建数个随机三角形，然后依次修改所有三角形的 u_time 属性，通过 setUniforms 方法将修改的属性更新到 shader 变量中。这样，我们就可以在 shader 中读取变量的值进行处理了。代码如下：

let triangles = [];

function update() {
  for(let i = 0; i < 5 * Math.random(); i++) {
    triangles.push(randomTriangles());
  }
  gl.clear(gl.COLOR_BUFFER_BIT);
  // 对每个三角形重新设置u_time
  triangles.forEach((triangle) => {
    triangle.u_time = (performance.now() - triangle.startTime) / 1000;
    setUniforms(gl, triangle);
    gl.drawArrays(gl.TRIANGLES, 0, position.length / 2);
  });
  // 移除已经结束动画的三角形
  triangles = triangles.filter((triangle) => {
    return triangle.u_time <= triangle.u_duration;
  });
  requestAnimationFrame(update);
}

requestAnimationFrame(update);

我们再回过头来看最终要实现的效果。你会发现，所有的三角形，都是由小变大朝着特定的方向旋转。那想要实现这个效果，我们就需要用到前面讲过的仿射变换，在顶点着色器中进行矩阵运算。

在这一步中，顶点着色器中的 glsl 代码最关键

attribute vec2 position;

uniform float u_rotation;
uniform float u_time;
uniform float u_duration;
uniform float u_scale;
uniform vec2 u_dir;

varying float vP;

void main() {
  float p = min(1.0, u_time / u_duration);
  float rad = u_rotation + 3.14 * 10.0 * p;
  float scale = u_scale * p * (2.0 - p);
  vec2 offset = 2.0 * u_dir * p * p;
  mat3 translateMatrix = mat3(
    1.0, 0.0, 0.0,
    0.0, 1.0, 0.0,
    offset.x, offset.y, 1.0
  );
  mat3 rotateMatrix = mat3(
    cos(rad), sin(rad), 0.0,
    -sin(rad), cos(rad), 0.0,
    0.0, 0.0, 1.0
  );
  mat3 scaleMatrix = mat3(
    scale, 0.0, 0.0,
    0.0, scale, 0.0,
    0.0, 0.0, 1.0
  );
  gl_PointSize = 1.0;
  vec3 pos = translateMatrix * rotateMatrix * scaleMatrix * vec3(position, 1.0);
  gl_Position = vec4(pos, 1.0);
  vP = p;
}

我们定义的 p 是当前动画进度，它的值是 u_time / u_duration，取值区间从 0 到 1。rad 是旋转角度，它的值是初始角度 u_rotation 加上 10π，表示在动画过程中它会绕自身旋转 5 周

其次，scale 是缩放比例，它的值是初始缩放比例乘以一个系数，这个系数是 p * (2.0 - p)，在我们后面讨论动画的时候你会知道，p * (2.0 - p) 是一个缓动函数，在这里我们只需要知道，它的作用是让 scale 的变化量随着时间推移逐渐减小就可以了。

最后，offset 是一个二维向量，它是初始值 u_dir 与 2.0 * p * p 的乘积，因为 u_dir 是个单位向量，这里的 2.0 表示它的最大移动距离为 2，p * p 也是一个缓动函数，作用是让位移的变化量随着时间增加而增大

定义完这些参数以后，我们得到三个齐次矩阵：translateMatrix 是偏移矩阵，rotateMatrix 是旋转矩阵，scaleMatrix 是缩放矩阵。我们将 pos 的值设置为这三个矩阵与 position 的乘积，这样就完成对顶点的线性变换，呈现出来的效果也就是三角形会向着特定的方向旋转、移动和缩放。

在片元着色器中着色

最后，我们在片元着色器中对这些三角形着色。我们将p也就是动画进度，从顶点着色器通过变量varying vP传给片元着色器，然后在片元着色器中让alpha值随着vP值变化，这样就能同时实现粒子的淡出效果了。

 precision mediump float;
  uniform vec4 u_color;
  varying float vP;

  void main()
  {
    gl_FragColor.xyz = u_color.xyz;
    gl_FragColor.a = (1.0 - vP) * u_color.a;
  }  

[5]CSS 的仿射变换

CSS 中的 transform 是一个很强大的属性，它的作用其实也是对元素进行仿射变换。

参考：

https://time.geekbang.org/column/intro/100053801?tab=catalog

https://www.3blue1brown.com/

https://www.bilibili.com/video/av6731067/?p=4

https://www.bilibili.com/video/BV1ib411t7YR?spm_id_from=333.337.search-card.all.click