Vellum —— 简介

挨代码

已于 2023-12-08 11:07:07 修改

阅读量1.5k

点赞数 15

分类专栏： # Vellum Houdini 文章标签： Houdini

于 2023-11-22 11:15:21 首次发布

本文链接：https://blog.csdn.net/NapoleonCoder/article/details/134413731

版权

Houdini 同时被 2 个专栏收录

119 篇文章

订阅专栏

Vellum

8 篇文章

订阅专栏

一，介绍

Vellum是一个解算模拟框架，使用更高级的PBD（XPBD，extended position based dynamics），是2nd Order Integration（传统的PBD使用的是1nd Order Integration），不像PBD子步和迭代次数影响刚性（迭代越多越硬）；由于Vellum Solver需对约束重复计算，为提高效率并行计算，引入Graph Color技术；Grain是使用PBD来模拟沙子或颗粒物的；

可被用于创建许多不同的东西，包括cloth、hair、softbodies、balloons、及grains；基于位置方法的主要优势，是其可控、稳定、快速生成可信结果；GPU友好对于并行约束解算，特别是使用graph color（Breaking Frequency会re-color）；

Constraint Iteration约束迭代，对于高刚性和高精度使用更高的约束迭代，提高子步效果更好但也更贵；Collision Iteration碰撞迭代，关联到detangle节点，在约束迭代间穿插执行；Smooth Iteration平滑迭代，默认约束迭代使用Gauss-Seidel方法快速收敛，对于不可能的配置（如无限刚性和0.5倍的restlength）等无法完全收敛的则使用Jacobi方法更慢的收敛来分散错误；

每个vellum类型均可相互交互，即可直接将各个类型的发射源合并（merge）起来，还可使用POP Force，POP Stream等；通常cloth使用三角面；

几种类型的柔体：

Cloth + Pressure，vellum configure balloon
Cloth + Structs，vellum configure struct softbody
Distance along edges + Tetrahedral volume
Tet Conform + Tetrahedral Stretch，vellum configure Tetrahedral softbody

对布线不均的模型，应remesh使对象均匀布线，以为后续解算，最后在用解算的对象驱动原模型；

注，按住J连接其中一个，三个输入/输出会自动一起连接；

二，原理

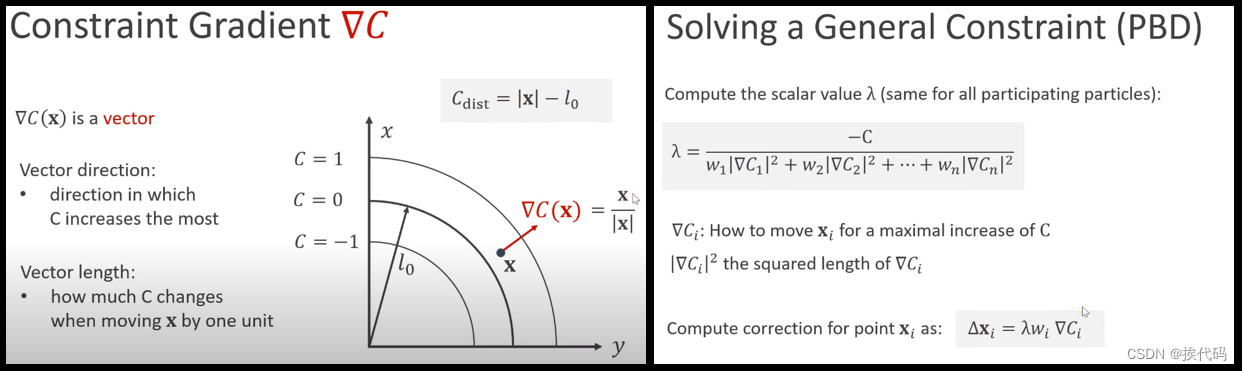
本质上是点（有碰撞半径的球）及约束组成，PBD是一个动态系统，试图一个点一个点地relax约束和碰撞，只有再足够高的迭代次数下才会产生合理的结果；

有三种类型的约束：Distance/Length/Stretch 保持点间的距离（可认为是线性弹簧），Rotational/Bend 保持面间的角度（可认为是旋转弹簧），Volume 保持几何体的体积（tetrahedron）；在实际应用中，可以是其中一种或多种的组合；

三，PBD算法

循环所有粒子，根据力及速度，计算新位置 $X_{i}$ ；
循环所有约束，修正新位置 $X_{i}$ ；
循环所有粒子，根据最终的位置和起始位置，更新速度 $V_{i}$

迭代iteration和子步sub-steps

【文献导读】XPBD: Position-Based Simulation of Compliant Constrained Dynamics_beidou111的博客-CSDN博客

【物理模拟】PBD算法详解-CSDN博客

手动实现PBD的拉伸

参考： Implementing A Position Based Cloth Solver From Scratch – Entagma

// Verlet Integration
vector cur_P = @P;
vector old_P = v@old_P;
vector force = v@force;

@P = 2*@P - old_P + force * pow(@TimeInc,2);

@old_P = cur_P;

//satisfy constraints
int constraints[] = pointprims(1, @ptnum);

vector displacement = set(0,0,0);
float weight = 0;

foreach(int con; constraints){
    int con_pts[] = primpoints(1, con);
    vector posa = point(0, 'P', con_pts[0]);
    vector posb = point(0, 'P', con_pts[1]);
    
    vector delta = posa - posb;
    float delta_len = length(delta);
    float restlength = prim(1, 'restlength', con);    
    float error = (restlength - delta_len) * 0.5;
    
    float dir = 1;
    if(con_pts[0] != @ptnum)
        dir = -1;
        
    displacement += normalize(delta) * error * dir;
    weight += 1.0;    
}

@P += displacement/weight;