1.简介
之前一直以为对BN是了解的,直到看了RepVGG文章中有一个结构重参数化部分,需要将BN算子融合到卷积算子中时,我才发现对BN的了解远远不够,所以现在来重新了解一下BN的整个计算流程。
我们可以发现,现在的网络模型中,基于卷积的神经网络99%都会用到BN,Transformer主要是LN,由此可见BN在整个网络结构中的重要性,几乎每经过一个卷积层后面都会跟着一个BN和激活函数层,那为什么要这样设计呢?对于这个问题的回答我觉得这篇文章写得非常好BN层的学习(意义、效果、训练测试的区别、数学公式推导、反向传播公式解释证明)_呆呆象呆呆的博客-CSDN博客_bn层公式
在神经网络训练开始前,都要对输入数据做一个归一化处理,那么具体为什么需要归一化呢?归一化后有什么好处呢?原因在于:
从训练和测试的角度来说:神经网络学习过程本质就是为了学习数据分布,一旦训练数据与测试数据的分布不同,那么网络的泛化能力也大大降低;
从训练中不同的batch来说:一旦每批训练数据的分布各不相同(batch 梯度下降),那么网络就要在每次迭代都去学习适应不同的分布,这样将会大大降低网络的训练速度,这也正是为什么我们需要对数据都要做一个归一化预处理的原因。
从网络结构敏感性来说:想要让输入尽可能的在权重和偏移作用下能输出一个使得激活层比较敏感的值,也就是说这个输出值最好能处在一个不是非常大的值,这也就是归一化的原因之一
对于网络深度来说1:对于深度网络的训练是一个复杂的过程,只要网络的前面几层发生微小的改变,那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变,那么这一层网络就需要去适应学习这个新的数据分布,所以如果训练过程中,训练数据的分布一直在发生变化,那么将会影响网络的训练速度。
对于网络深度来说2:网络在训练过程中,参数就要发生更新,除了输入层的数据外(因为输入层数据,我们已经人为的为每个样本归一化),后面网络每一层的输入数据分布是一直在发生变化的(因为前面一层的参数已经变化,相对于之前的结果已经变化了,属于不同的分布了),因为在训练的时候,前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例:网络的第二层输入,是由第一层的参数和input计算得到的,而第一层的参数在整个训练过程中一直在变化,因此必然会引起后面每一层输入数据分布的改变。我们把网络中间层在训练过程中,数据分布的改变称之为:“Internal Covariate Shift”。Paper所提出的算法,就是要解决在训练过程中,中间层数据分布发生改变的情况,于是就有了Batch Normalization,这个牛逼算法的诞生。
2.BN的数学表达式
就像激活函数层、卷积层、全连接层、池化层一样,在前面我们提到网络除了输出层外,其它层因为低层网络在训练的时候更新了参数,而引起后面层输入数据分布的变化。这个时候我们可能就会想,如果在每一层输入的时候,再加个预处理操作那该有多好啊,比如网络第三层输入数据X3(X3表示网络第三层的输入数据)把它归一化至:均值0、方差为1,然后再输入第三层计算,这样我们就可以解决前面所提到的“Internal Covariate Shift”的问题了。
而事实上,paper的算法本质原理就是这样:在网络的每一层输入的时候,又插入了一个归一化层,也就是先做一个归一化处理,然后再进入网络的下一层。不过文献归一化层,可不像我们想象的那么简单,BN是一个可学习、有参数的网络层。
2.1引入了可学习的参数来进行变换重构
BN引入了可学习参数γ、β,针对归一化后的值进行再一次的变换重构,这就是算法的关键之处:
![]()
每一层、每个通道都会有一个γ、β参数。

这样我们就可以通过网络自身的学习γ、β参数,来重构出原始网络所要学习的特征分布,BN层中只有γ、β参数是可学习的参数,均值和方差都是通过输入来计算得到的。

3.BN的应用
BN层在训练和测试的过程中是不一样的。训练时输入的每个batch的均值和方差都是不一样的,γ和β参数也是不断在更新的。测试时所有参数都是固定不变的,不论输入的是多少,其中的均值、方差、γ和β参数都是不变的。
训练的时候会记录训练集中每一个mini-batch的均值和标准差 ,然后用来推测出测试集中应该用于归一化测试集输入数据的均值μ,标准差σ。
1)对于均值来说直接计算所有mini-batch的记录的本次batch均值μ的平均值
2)对于标准偏差采用每个mini-batch标准差σ的无偏估计
以此推断出来的均值和标准差来作为测试样本所需要的均值、标准差。最后测试阶段的均值μ 和标准差σ计算公式如下:
测试时,BN的计算公式为:

![]() 偏置参数b经过BN层后其实是没有用的,最后也会被均值归一化,当然BN层后面还有个β参数作为偏置项,所以b这个参数就可以不用了。因此最后把BN层+激活函数层就变成了:
偏置参数b经过BN层后其实是没有用的,最后也会被均值归一化,当然BN层后面还有个β参数作为偏置项,所以b这个参数就可以不用了。因此最后把BN层+激活函数层就变成了:![]() 。注意:假如输入是3个通道,就是在通道的维度上进行bn,所以会有3个γ,β参数。
。注意:假如输入是3个通道,就是在通道的维度上进行bn,所以会有3个γ,β参数。
4.BN的反向传播
BN的反向传播与普通的全连接网络差不多,都是通过链式法则来求解,只不过这里的公式稍微多一点,就是依靠前面的这四个公式:

通过链式法则就能够求解出以下6个偏导:
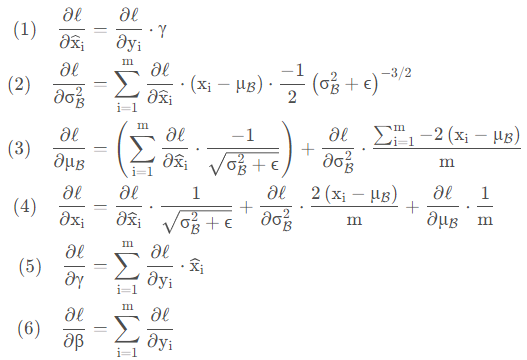
5.总结
如果以上的你懂看明白的话,BN你就理解的差不多了。BN层就是用在激活函数前,用来使上一层的输出,分布在均值为0,方差为1的情况下,也就是对下一层的输入做归一化的操作,这样就能够使它经过激活函数时能够有一定的梯度,从而避免值太大而进入饱和区,梯度就非常小了,不利于梯度下降。并且除了均值和方差,BN层还有自己的学习参数γ和β,网络通过学习来得到想要的数据分布,参数γ和β在训练中通过反向传播中的γ与β求得梯度,从而不断改变每个通道的γ和β参数。最终训练完后,利用所有batch的均值和方差再求出均值和方差,γ和β参数不再变化。通过这四个参数最终确定BN层的输出。
以上就是关于BN的所有内容了,谢谢观看,希望能帮助到你们。

























 605
605

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








