切线空间切向量计算

这一次主要是对切线空间和法线贴图相关知识的个人理解和分享。

首先我们考虑一个三角形，要为这个三角形内的每一个像素都给定一个法线向量 ，这个三角形是一个平面，有一个平面法向量，我们可以修改这个向量去定义每个像素的法向量，例如每个像素上向某个轴偏移一个值，向另一个轴偏移一个值。这两个轴最好都垂直于该平面法线 但问题是， 那另外两个轴如何确定呢，这是一个常见的三维问题，给定一个轴，另外两个轴有无限种可能。

针对上述情况，比较简单的方式就是利用纹理坐标来确定另外两个轴的方向，下面是一些理解 ：

1.有一个向量，该向量指向（uv坐标的）U值在三角形上增加的方向，那么它在模型空间坐标系中的坐标将是多少
2.模型空间X，Y，Z轴坐标相对于UV坐标的变化率。也就是说 切线（Tangent）向量实际上是模型空间坐标相对于U值分量的变化率，而副切线（Bitangent）向量则是模型空间坐标相对于V值分量的变化率
3.可以假设在tb平面上贴一张平面图，t->u,b->v,我们当前的点，则是对应uv图上的某一个点，所以可以理解为：在这个点将uv图展开，我们的tb方向就是此时的uv方向，对应的纹理的点也很明显

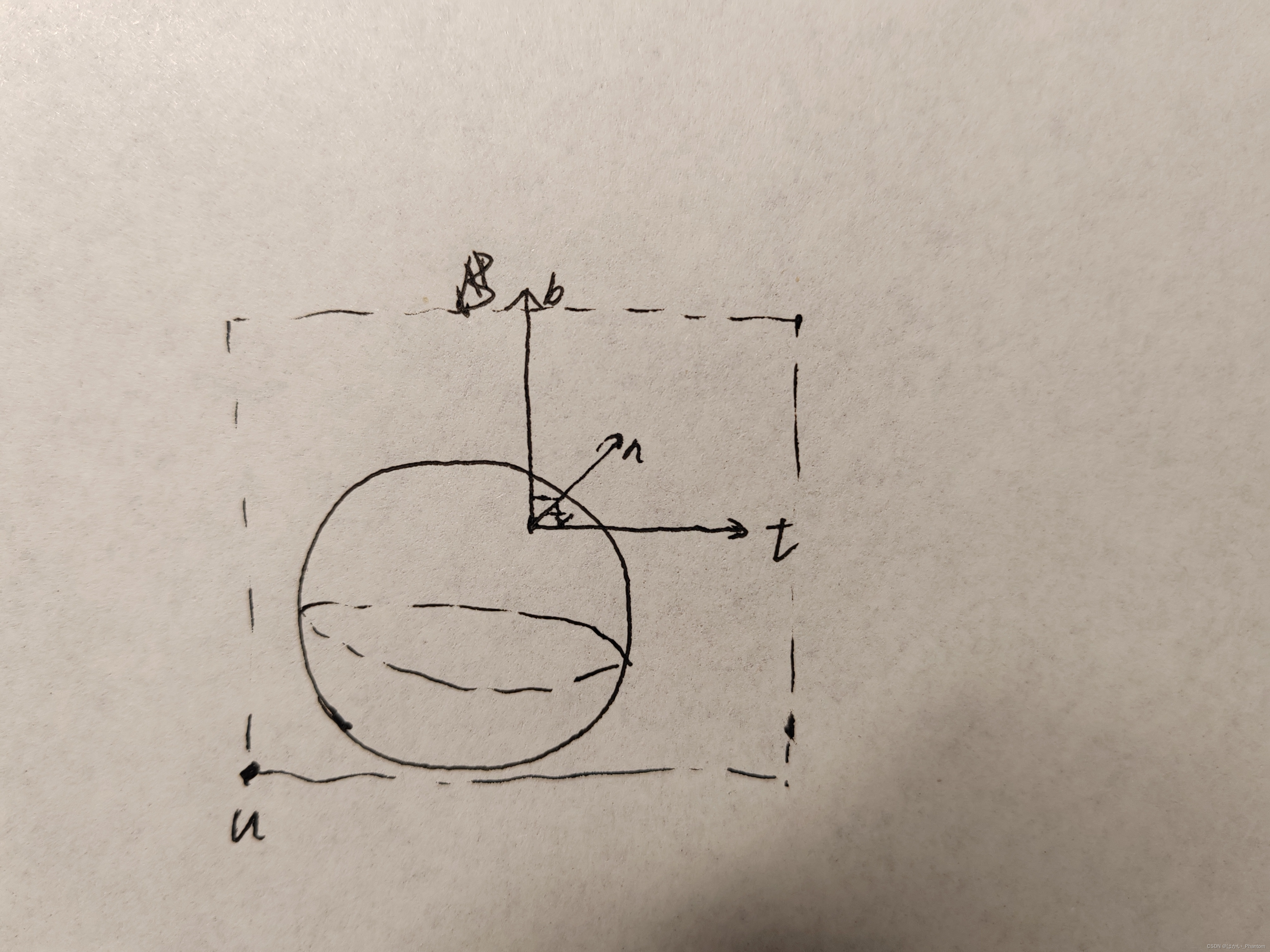
所以现在的问题是怎么样求得t和b的向量，这即是最近一直困扰我的问题，将二维映射到三维。
具体的解决思路如下：
我们的目的是求得tb的向量，可以假设有一个三角形在切线空间的tb平面uv图上，如下图，可以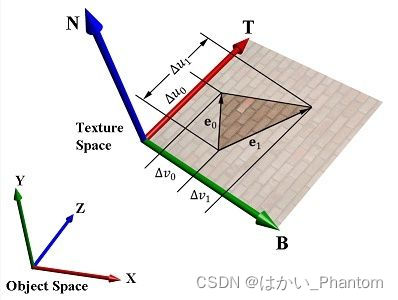
进行如下的计算:

如上图：t可以分为(tx,ty,tz),说明此时t的表示是在模型空间中的表示！！