《机器学习》实验四：利用SVM模型实现判断病人是否属于糖尿病

UestcXiye

已于 2023-02-21 09:41:39 修改

阅读量1.5k

点赞数

分类专栏：机器学习文章标签：机器学习支持向量机人工智能

于 2022-11-22 18:35:52 首次发布

本文链接：https://blog.csdn.net/ProgramNovice/article/details/127987709

版权

机器学习专栏收录该内容

11 篇文章

订阅专栏

本实验运用支持向量机(SVM)模型对糖尿病患者数据进行分类分析。采用sklearn库进行数据预处理、训练及测试，最终模型准确率达到78.87%，验证了SVM在医疗诊断中的有效性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

《机器学习》实验四：利用SVM模型实现判断病人是否属于糖尿病

《机器学习》实验四：利用SVM模型实现判断病人是否属于糖尿病

《机器学习》实验四：利用SVM模型实现判断病人是否属于糖尿病

实验目的

掌握支持向量机的基本原理；
了解机器学习库sklearn。

实验原理

支持向量机
支持向量机（Support Vector Machine, SVM）是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面，可以将问题化为一个求解凸二次规划的问题。具体来说就是在线性可分时，在原空间寻找两类样本的最优分类超平面。在线性不可分时，加入松弛变量并通过使用非线性映射将低维度输入空间的样本映射到高维度空间使其变为线性可分，这样就可以在该特征空间中寻找最优分类超平面。与逻辑回归和神经网络相比，SVM可以通过核方法（Kernel Method）进行非线性分类，是常见的核学习（Kernel Learning）方法之一，在学习复杂的非线性方程时提供了一种更为清晰，更加强大的方式。
在分类问题中给定输入数据和学习目标：
$X={X_1,X_2,…,X_n }$
$y={y_1,y_2,…,y_n }$
其中，输入数据的每个样本都包含多个特征并由此构成特征空间： $X_i=[x_1,x_2,…,x_n]∈χ$ ，而学习目标为二元变量 $y∈{-1,1}$ ，表示负类和正类。
若输入数据所在的特征空间存在作为决策边界的超平面：
$w^T X+b=0$
并将学习目标按正类和负类分开，并使任意样本的点到平面距离大于等于1：
$y_i (w^T X_i+b)≥1$
则称该分类问题具有线性可分性，参数w和b分别为超平面的法向量和截距。
如图1所示，满足该条件的决策边界实际上构造了2个平行的超平面作为间隔边界以判别样本的分类：
$w^T X_i+b≥+1⟹y_i=+1$
$w^T X_i+b≤-1⟹y_i=-1$
所有在上间隔边界上方的样本属于正类，在下间隔边界下方的样本属于负类。两个间隔边界的距离d=2/‖w‖ 被定义为边距，位于间隔边界上的正类和负类样本为支持向量。

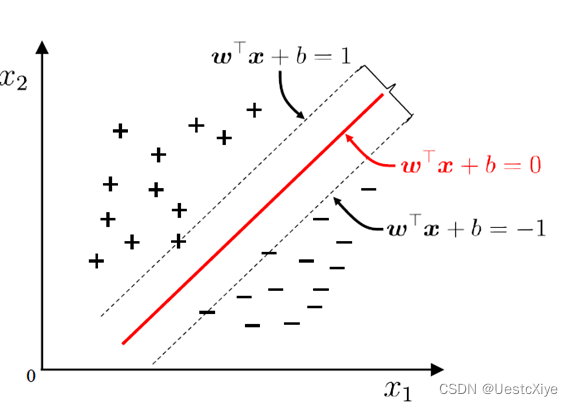
在这里插入图片描述

图1 支持向量机线性分类

机器学习库sklearn
Scikit-learn（以前称为scikits.learn，也称为sklearn）是针对Python 编程语言的免费软件机器学习库。它具有各种分类，回归和聚类算法，包括支持向量机，随机森林，梯度提升，k均值和DBSCAN，并且旨在与Python数值科学库NumPy和SciPy联合使用。

实验内容与要求

数据预处理；
数据标准化处理；
训练SVM模型；
绘制图像。

实验器材（设备、元器件）

处理器：Intel® Core™ i5-8300H CPU @ 2.30GHz
Python 3.9.0
matplotlib 3.4.0
sklearn 0.0
xlrd 1.2.0

实验步骤

数据预处理
给定的训练集和测试集是data文件，先把它们改为xlsx文件。设计一个LoadData函数，输入为diabetes_train.xlsx和diabetes_test.xlsx的文件路径，再调用Python第三方库——xlrd，将当中的数据转换为列表x_train、y_train、x_test、y_test，最后返回这四个列表。代码如下：

def LoadData(trainpath, testpath):
    file_train_path = trainpath
    file_train_xlsx = xd.open_workbook(file_train_path)
    file_train_sheet = file_train_xlsx.sheet_by_name('Sheet1')
    x_train = []
    y_train = []
    for row in range(file_train_sheet.nrows):
        x_data = []
        for col in range(file_train_sheet.ncols):
            if col < file_train_sheet.ncols - 1:
                x_data.append(file_train_sheet.cell_value(row, col))
            else:
                if file_train_sheet.cell_value(row, col) == 'tested_negative':
                    y_train.append(0)
                else:
                    y_train.append(1)
        x_train.append(list(x_data))

    file_test_path = testpath
    file_test_xlsx = xd.open_workbook(file_test_path)
    file_test_sheet = file_test_xlsx.sheet_by_name('Sheet1')
    x_test = []
    y_test = []
    for row in range(file_test_sheet.nrows):
        x_data = []
        for col in range(file_test_sheet.ncols):
            if col < file_test_sheet.ncols - 1:
                x_data.append(file_test_sheet.cell_value(row, col))
            else:
                if file_test_sheet.cell_value(row, col) == 'tested_negative':
                    y_test.append(0)
                else:
                    y_test.append(1)

        x_test.append(list(x_data))

    # print(x_train)
    # print(y_train)
    # print(x_test)
    # print(y_test)
    return x_train, y_train, x_test, y_test

数据标准化处理
在将训练集和测试集导入SVM模型之前，要对训练集和测试集的数据进行归一化处理。代码如下：

# 分别初始化对特征值和目标值的标准化器
ss_x = StandardScaler()
ss_y = StandardScaler()
# 训练数据都是数值型，所以要标准化处理
x_train = ss_x.fit_transform(x_train)
x_test = ss_x.fit_transform(x_test)
# 目标数据也是数值型，所以也要标准化处理
y_train = ss_y.fit_transform(np.array(y_train).reshape(-1, 1))
y_test = ss_y.fit_transform(np.array(y_test).reshape(-1, 1))

训练SVM模型
使用LinearSVC分类训练，参数均未设置，默认为初始值。代码如下：

# 使用LinearSVC分类训练
linear_svc = LinearSVC()
linear_svc.fit(x_train, y_train.astype('int'))
linear_svc_predict = linear_svc.predict(x_test)

绘制图像
在run.py中绘制支持向量机回归预测图像。代码如下：

# 绘图
l1, = plt.plot(y_test, color='b', linewidth=2)
l2, = plt.plot(linear_svc_predict, color='r', linewidth=2)
plt.legend([l1, l2], ['y_test', 'linear_svc_predict'], loc=2)
plt.savefig('支持向量机回归预测.jpg')
plt.show()

实验结果
编写好代码后，运行run.py。
运行结果如图2所示。

在这里插入图片描述

图2 运行结果

支持向量机回归预测如图3所示。其中，蓝色折线是测试集的标签，红色折线是预测标签。

在这里插入图片描述

图3支持向量机回归预测

在本次实验中，使用线性SVM分类器LinearSVC进行分类训练，测试集的准确率为0.788659793814433，预测成功率在50%以上，实验成功。

心得体会

本实验利用SVM模型实现判断病人是否属于糖尿病，使用了机器学习库sklearn中的线性SVM分类器LinearSVC进行分类训练，测试集的准确率为0.788659793814433，达到预期目标。通过此次实验，很好地掌握了支持向量机的基本原理，熟悉了Python第三方库——sklearn、matplotlib和xlrd的使用。