半导体器件与物理篇2 载流子输运现象

迁移率mibility

迁移率的定义：用来描述载流子在单位电场下运动快慢的物理量

电子迁移率的表达式：${\mu }_n=\frac{q{\tau }_c}{m_n}$
空穴迁移率的表达式：${\mu }_p=\frac{q{\tau }_c}{m_p}$
两个迁移率有相同的变化方式，就是在同一温度下，迁移率随杂质浓度的增加而减少。电子迁移率往往高于空穴迁移率。
定义的话，大家先捏着鼻子记忆一下。想进入这个领域，就得把前人的东西记住一些。

由能量均分理论能得到电子的动能为$\frac{1}{2}{m}_n{v}_{th}^2$
$m_n$为电子的有效质量，$v_{th}$为平均热运动速度。

室温(300K)下的$v_{th}$，在硅和砷化镓中，约为$10^{-7}c{m}^{-3}$

##载流子漂移
电子与各种散射中心碰撞，经过足够长的时间，净位移为0。
碰撞间平均的距离叫平均自由程$l$，典型值为$10^{-5}cm$
碰撞间平均的时间叫平均自由时间${\tau }_c$，典型值为1ps，也就是$10^{-12}$s
平均自由时间取倒数得到单位时间内发生碰撞的次数$\frac{1}{{\tau }_c}$：
$\frac{1}{{\tau }_c}=\frac{1}{{\tau }_{c,晶格}}+\frac{1}{{\tau }_{c,杂质}}$
$\frac{1}{{\tau }_{c,晶格}}$是单位时间电子与晶格碰撞的次数，$\frac{1}{{\tau }_{c,杂质}}$是单位时间内电子与杂质碰撞的次数
由于q和m相同，所以可以对单位时间内发生碰撞的次数进行化简，得到迁移率的关系：$\frac{1}{\mu }=\frac{1}{{\mu }_l}+\frac{1}{{\mu }_i}$

电子是不安分的，在没有电场力等其他作用时，电子会因为热运动等一直不断地与各种散射中心碰撞。施加电场$E$后，电子会沿电场反向加速（因为电子带负电）。
漂移电流：在外加电场的作用下，载流子运输产生的电流就叫做漂移电流。
施加电场$E$后，电子会沿电场反向加速，此时获得的加速分量为漂移速度。

以电子为例，由动量定理（质量乘以速度=力乘以施加的时间）得到：$v_n{m}_n=-q{\tau }_{c}E$
对上式进行变换，可以得到$v_n$的表达式：$v_n=\frac{-q{\tau }_{c}E}{m_n}$
大家都知道时间乘以速度等于路程，所以由漂移速度可以得到漂移运动。
漂移运动的定义：漂移运动是在外电场作用下载流子的定向运动。
由$\mu =\frac{q\tau }{m}$可以得到电子漂移速度：$v_n=-{\mu }_{n}E$
空穴漂移速度：$v_p={\mu }_{p}E$

散射机制

首先，让我们回顾一下上一章的这个公式。

$\frac{1}{{\tau }_c}=\frac{1}{{\tau }_{c,晶格}}+\frac{1}{{\tau }_{c,杂质}}$
$\frac{1}{{\tau }_{c,晶格}}$，是单位时间电子与晶格碰撞的次数，$\frac{1}{{\tau }_{c,杂质}}$是单位时间内电子与杂质碰撞的次数

可以看到，电子会和晶格、杂质原子相碰撞。想象一下打保龄球，电子与晶格、杂质原子的碰撞有点类似于这个。
由引用的公式可以得到，散射机制会通过这个公式的右侧，从而影响公式的左侧变量，也就是${\tau }_c$。间接地，散射机制就会影响到迁移率$\mu$

散射机制主要有两种，分别是晶格散射lattice scattering和杂质散射impurity scattering

晶格散射lattice scattering

晶格散射的产生原因是晶格原子的热运动。
就像美国的两党一样，一党式微，另一党就如日中天。

那么，晶格散射什么时候占据主导地位呢？
晶格散射主导的区间：高温、低掺杂的时候。原因是温度越高，热振动越强。
晶格散射对迁移率的影响：迁移率随温度上升而降低。定量的表达则是${\mu }_L$随$T_{-3/2}$而下降。这里的${\mu }_L$中的$L$来自于"Lattice scattering"中的L

杂质散射

杂质散射的产生原因：带电载流子经过电离杂质引起的（受电离杂质周围的力影响）
杂质散射主导的区间：低温、高掺杂时
杂质散射随温度的变化：温度升高而该散射的有效性降低。
杂质散射对迁移率的影响：在同一温度下，迁移率随杂质浓度的上升而降低。定量的描述是${\mu }_I$随$\frac{T_{\frac{3}{2}}}{N_T}$而改变（$N_T$为总杂志浓度）

注意一个很重要的知识点，这将在下一道例题中加以使用：
杂志散射时，对于低浓度的杂质，几乎所有位于浅能级的施主杂质(doner,提供电子的杂质)和受主杂质(acceptor,提供空穴的杂质)都全部电离，因此可以得到$杂质浓度=载流子浓度$

电阻率

什么是电阻率呢？你只要知道，电阻率越大，他就越会拖电子的后退，不让他移动。

半导体的电导率表达式为：$\sigma =\frac{J}{E}=q(n{\mu }_n+p{\mu }_p)$
电阻率$\rho$为电导率$\sigma$的倒数：$\rho =\frac{1}{\sigma }=\frac{1}{q(n{\mu }_n+p{\mu }_p)}$

一般情况下，我们可以想像在半导体内部，电场一直沿着负梯度拉着电子；而电阻不断阻碍电子被拉走。

当一电场E施加于半导体上，每一个电子将会在电场中受到一个-qE的力，这个力等于电子电势能的负梯度，即：$-qE=-\frac{d{E}_C}{dx}$

已知在外加电压的作用下，各能级会呈现如下的变化：

由于导带底部$E_C$相当于电子的电势能，对电势能梯度而言，可用与$E_C$平行的本征费米能级$E_i$的梯度来代替，即：$E=\frac{1}{q}\frac{d{E}_C}{dx}=\frac{1}{q}\frac{d{E}_i}{dx}$
引入静电势，其负梯度等于电场，即:$E=-\frac{d\psi }{dx}$
因此有$\psi =-\frac{E_i}{q}$

电阻率的推导过程

电阻率的获得可并不简单，它涉及很多其他概念的普及。
我们跟随前人的思路，了解一下电阻率的推导过程。且为了简化，仅考虑漂移作用，也就是运用至此为止本章所学习的知识点。

推导过程：
1.电子电流密度等于总电流与横截面积之比，定量描述为：$J_n=\frac{I_n}{A}$
电子电流密度还等于单位面积上所有电子的电荷与速度之积：${\sum }_{i=1}^n(-q)\cdot v_i$
累加是不容易计算的，我们用一个平均速度来代替累加，并用$n$表示该单位面积下的电子总数：$-qn{v}_n$
上式中存在负号，是因为电子的速度方向和电流方向相反。
电子的定向速度是因为由电场力的作用，可以得到电子的平均速度$v_n$与迁移率${\mu }_n$、电场强度$E$的关系:$v_n=-{\mu }_{n}E$
上式中存在负号，是因为n为电子，所以是电子的受力方向与e相反
将$v_n=\mu E$代入$J_n=-qn{v}_n$得到：$J_n=qn{\mu }_{n}E$
2.空穴$J_p$的推导同理。
获取后于$J_n$合并，得到：$J=J_n+J_p=(qn{\mu }_n+qp{\mu }_p)E$
3.电导率$\sigma$就是材料在单位电场$E$下对电子运动的促进能力，也就是说电导率$\sigma$越大，总电流密度$J$越大。$\sigma =\frac{J}{E}=q(n{\mu }_n+p{\mu }_p)$
电阻率$\rho$为电导率$\sigma$的倒数：$\rho =\frac{1}{\sigma }$
4.一般而言，对于不同的非本征半导体，我们只抓住主要矛盾。也就是说在掺杂的非本征半导体中，我们在其电导率$\sigma$的表达式中仅保留其中占主导作用的一项，可能是空穴，也可能是电子

四探针法

四探针法的计算公式为：$\rho =\frac{V}{I}\cdot W\cdot CF$
电压测量值$V$，电流测量值$I$，半导体厚度$W$，校正系数$CF$

在以上变量中，只有校正系数$CF$的含义不明确。但你也不必惊慌，他可以由另外两个可以直接观测到的变量进行估算。它们分别是样品直径$d$和探针间距$s$（PS：四探针的最左侧和最右侧距离为$3s$）

当$\frac{d}{s}>20$时，$CF$-约为4.54

霍尔效应

霍尔效应的定义：当电场力$Eq$与洛伦兹力$q{v}_x{B}_z$相同时半导体内部达到平衡，并在半导体的y方向上产生一电势差$V_H$。该现象为霍尔效应，所以霍尔效应本质是一个现象，上一句这么一大串都是对这个现象的修饰。
霍尔效应的意义：

求霍尔系数的表达式

用一块以空穴为多数载流子的半导体为例，求霍尔系数$R_H$：

求霍尔系数$R_H$就是在半导体材料其他条件都相同的情况下,衡量其产生电场的能力。
既然要保证其他条件相同，就需要采用控制变量法。

那么，控制哪些变量呢？
已知电场发生在$y$方向上，那么我们一般控制$x$方向上的电流速度$v_x$(这里用电流密度$J$来代替表示)和$z$方向上的磁场强度$B_z$。
由此，我们求得电场强度$E_y$的表达式后，将电流密度$J$和磁场强度$B_z$去除，就可以判断一块半导体材料在电流密度相同、磁场相同的情况下在$y$方向上产生电势差$V_H$或电场$E_y$的能力

1.已知空穴电流密度$J_p=qp{\mu }_{p}E=qp{v}_p$
$v_p$是众多空穴漂移的平均速度
将上式转化为平均速度$v_p$的表达式得到：$v_p={\mu }_{p}E=\frac{J_p}{qp}$
2.由于空穴沿x方向运动，故$v_x=v_p$
代入$q{E}_y=q{v}_x{B}_z$得$E_y=v_p{B}_z$
在将平均速度$v_p$的表达式代入上式得到：$E_y=\frac{J_p}{qp}{B}_z$
3.去掉电场强度$E_y$表达式中的电流密度和磁场强度$B_z$，相当于是取出$\frac{1}{qp}$，得到$R_H=\frac{1}{qp}$
这里注意一下，如果我们用一块以电子为多数载流子的半导体为例，那么其霍尔系数为$R_H=-\frac{1}{qn}$。即p型半导体的霍尔系数为正，n型半导体的霍尔系数为负。

如此，我们就求得了$y$方向上的霍尔电压$V_H$和电场强度与哪些变量有关。
但是各位实际思考一下，对于一块已知的半导体材料来说，是它的电场强度$E_y$或者上下y方向上的电势差$V_H$难求，还是它内部的电载流子密度$p$或$n$难求？
显然是后者，因此求霍尔系数$R$只不过是开胃菜罢了，我们真正需要的是使用电势差或电场强度等变量求得载流子密度

利用霍尔效应求载流子浓度

1.由$E_y=\frac{J_p}{qp}{B}_z$得$p=\frac{1}{q{R}_H}=\frac{J_p{B}_z}{q{E}_y}$
2.已知匀强电场内，电势差等于电场乘以距离：$E_y=\frac{V_H}{W}$
电势差$V_H$;电场强度$E_y$;半导体材料在y方向的宽度W
3.电流密度$J$并不好求，但是电流$I$很好求,并且半导体材料的截面积$A$也很好求。因此，我们使用电流大小和截面积来代替电流密度$J_p=\frac{I}{A}$
4.综合第2.3步，最终可以求得载流子浓度为（n型、p型共用）：$p==\frac{J_p{B}_z}{q{E}_y}=\frac{\frac{I}{A}{B}_Z}{q\frac{V_H}{W}}=\frac{I{B}_{z}W}{q{V}_{H}A}$

扩散电流diffusion current

扩散电流的定义：在半导体中，载流子浓度在空间上有变化时，倾向于从高浓度区域移到向低浓度区域，因而产生的电流为扩散电流

扩散电流的计算公式包括电子扩散电流密度：$J_n=-qF=q{D}_n\frac{dn}{dx}$
和空穴扩散电流密度：$J_p=qF=q{D}_p\frac{dp}{dx}$
净电子流$F$，也称为载流子的净速率，其计算方式：电子浓度大处扩散的速度与电子浓度小处扩散的速度在电子浓度中间处的差；$扩散系数D_n=热平衡下电子的平均运动速度v_{th}\cdot 平均自由程l$

爱因斯坦关系式：$\frac{D_n}{kT}=\frac{{\mu }_n}{q}$

爱因斯坦关系式的意义是将描述半导体中载流子的扩散与漂移运动特征的两个重要常数联系了起来，即将扩散系数和迁移率联系了起来。
将爱因斯坦关系式转化为扩散系数的表达式，可以得到：$D_n=\frac{kT}{q}{\mu }_n$

电流的真实运动方式

我们在上文中探讨了电子或空穴，分别做漂移运动和扩散运动时产生的电流密度。
可现实中往往是扩散与漂移同时进行的。
我们先来辨析一下漂移运动和扩散运动。

就源动力的而言，漂移运动的源动力来自于电场$E$，它是被电场牵引所产生的载流子的运动；扩散运动的源动力则来自于浓度梯度$\frac{dn}{dx}$

先普及一点，不同材料对于源动力的利用能力，即是表达式中乘在源动力变量之前的各个系数。

那么漂移运动中载流子对电场的利用能力，是用迁移率$\sigma$来表示的；而扩散运动中载流子对浓度梯度的利用能力，则是用扩散系数$D_n$来表示

而总的电流密度$J_{cond}$都与电荷量有关，因此我们需要牢记一个电子的带电量$q=1.6\cdot 10^{-19}C$

根据以上的分析，我们得到电子的电流密度的表达式$J_n=q{\mu }_{n}E+q{D}_n\frac{dn}{dx}$

空穴的电流密度表达式：$J_n=q{\mu }_{p}E-q{D}_p\frac{dp}{dx}$
两者相结合，得到在低电场状态下总电流密度的表达式：$J_{cond}=J_n+J_p=q{\mu }_{n}E+q{D}_n\frac{dn}{dx}+q{\mu }_{p}E-q{D}_p\frac{dp}{dx}$
以上表达式仅适用于低电场状态下
若处于高电场状态，${\mu }_{n}E$和${\mu }_{p}E$应该使用饱和速度$v_s$代替

非平衡状态nonequilibrium situation

非平衡状态的态的定义：有过剩载流子引入半导体中，使$p\cdot n>n_i^2$
如何引入这些过剩载流子的呢？通过载流子注入(carrier injection)。

载流子注入：引入过剩载流子的过程，如光激发等
任何事物都不希望保持不稳定的状态。放在高空中的花瓶有向下掉落的趋势，劳累了一天的上班族有回到床上休息的趋势，半导体中过剩的载流子也有回归平衡的趋势。
而这个平衡就是$p\cdot n>n_i^2$

那么如何从非平衡状态逐步回归到平衡状态呢？
答案是，通过复合！

复合

复合的定义：一个电子从导带向下跃迁至价带，一个电子-空穴对消失的过程
复合的分类：

分类方式	复合类型
按过程释放能量	辐射负荷：能量以光子形式辐射出去的复合过程。
–	非辐射复合：能量以晶格产生热而消耗掉的负荷过程。
按有无复合中心	直接复合：带自带间进行的符合。
–	间接复合：通过禁带复合中心进行的符合。

直接复合direct recombination

直接复合是在不改变动量$p$的情况下，电子从跃迁到导带的状态回归到价带中
有复合的前提是有产生，所以我们先来探讨一下载流子的产生。

载流子产生的定义：热平衡状态下的直接带隙半导体中，热能使一个价电子向上跃迁至导带，而在价带中产生一个空穴的过程（也就是同时有一对电子和空穴发生了能带的跃迁）。

我们一般用产生速率$G_{th}$定量描述载流子的产生。$G_{th}$中的G是“generate”的意思，而th是“thermal equilibrium热平衡”的意思。
产生速率$G_{th}$的定义：半导体中每立方厘米每秒产生的电子-空穴对数目

了解了基本概念以后，让我们分析一下直接复合的整个过程。

直接复合的过程

1.首先，一块半导体在所有实验开始前，都是处于平衡状态的。
在热平衡状态时，$热平衡时的载流子产生速率G_{th}=热平衡时的复合速率R_{th}$
复合的定义：一个电子从导带向下跃迁至价带，一个电子-空穴对小时的过程。
复合速率$R_{th}$中的R表示“recomposite”，正比于导带中电子浓度$n$与价带中空穴浓度$p$(PS:导带中的电子，和价带中的空穴都是具有一定能量的载流子了)，其数学表达式为：$R_{th}=\beta n_{n0}{p}_{n0}$
$\beta$为比例系数；$n_{n0}$指热平衡"0"时n型半导体中的电子浓度n，也就是多子浓度；$p_{n0}$指热平衡"0"时n型半导体中的空穴浓度p，也就是少子浓度
2.此时进行载流子注入。载流子注入后变为非平衡状态。
非平衡状态时，复合速率依旧是由半导体中的多子与少子浓度决定，只不过两个浓度不再是平衡状态的浓度：$R=\beta np$
而非平衡状态下载流子产生速率则由两部分组成：$G=G_L+G_{th}$
$G_L$中的L是“light光”的意思，因此$G_L$是光激发产生的电子-空穴对。
当然，如果是不只有光激发的时候，$G_L$就不足以代表载流子的产生速率。此时我们会用新的变量来表示产生速率，也就是净复合率$U$：$U=G_L+...=G-G_{th}$
净复合率$U$是将平衡时的载流子产生速率$G_{th}$从总体载流子产生速率$G$的表达式中去除的载流子产生速率。
对空穴而言，净复合率正比于过剩载流子的浓度。因此通过复杂的计算过程（过程略）可以得到其另一个表达式：$U=\frac{p_n-p_{n0}}{{\tau }_p}$
$p_{n0}$中的“0”指热平衡状态。

${\tau }_p$为"过剩的少子寿命(life time)"，其表达式为：${\tau }_p=\frac{q}{\beta n_{n0}}$

由“过剩的少子寿命”的表达式可以看出，它只与多子在热平衡时的浓度$n_{n0}$有关。因此只要在热平衡时测得$n_{n0}$，便可以用来辅助计算非平衡状态的各个参数。

净复合率的大小是被半导体材料本身所决定的，但载流子浓度却是在它从非平衡走向平衡的过程中时刻都在变化的。

现实中我们求解的思路就是用简单的、不变的量去求解复杂的、变化的量。
因此我们往往通过净负荷率来计算载流子浓度。

求解半导体中少子的浓度，所利用的公式为：$p_n=p_{n0}+{\tau }_{p}U$
当半导体只受光激发作用时，可以得到载流子的浓度与光激发产生的电子空穴对之间的关系：$p_n=p_{n0}+{\tau }_p{G}_L$

间接复合

间接符复合的定义：通过中间能态(即复合中心)而发生的各种跃迁。你可以想象成：电子无法一步踏到所要跃迁的能态，所以在中间去踩了一下垫脚石，帮助他进行跃迁。

间接复合按过程分类，包括：电子俘获，电子发射，空穴俘获，空穴发射。电子俘获:导带中的电子被禁带中的中性复合中心俘获；电子发射:复合中心上的电子跃迁回导带；空穴俘获:价带中的空穴被带负电的复合中心俘获；空穴发射:复合中心向价带发射了一个空穴。

一般也用复合率$U$来描述复合速度的大小，和间接复合的各种复合过程。

以n型半导体为例，间接复合中复合率的表达式：$U=v_{th}\cdot \frac{{\sigma }_n{\sigma }_p{N}_t(p_n{n}_n-n_i^2)}{{\sigma }_p[p_n+n_{i}exp(\frac{E_i-E_t}{kT})]+{\sigma }_n[n_n+n_{i}exp(\frac{E_t-E_i}{kT})]}$

我们可以看到，上面这个表达式相当地复杂。
如何拆解呢？

1.首先，我们先了解这些变量各自的含义，然后再分析它们组合起来，各自表示什么含义。

变量含义	符号表示
载流子热运动速度	$v_{th}$
电子俘获截面	${\sigma }_n$
空穴俘获截面	${\sigma }_p$
半导体中复合中心的浓度	$N_t$
复合中心的能级位置	$E_t$
本征费米能级	$E_i$

2.理解式子时，我们要明确一点，复合率本质上是速率。
因此，我们将它与平衡时载流子的热运动速率进行比较。

右边的一大串分式$\frac{{\sigma }_n{\sigma }_p{N}_t(p_n{n}_n-n_i^2)}{{\sigma }_p[p_n+n_{i}exp(\frac{E_i-E_t}{kT}]+{\sigma }_n[n_n+n_{i}exp(\frac{E_t-E_i}{kT})]}$只不过是在求间接复合（也就是对于间接带隙半导体的不平衡状态）的情况下，载流子进行复合的速率相比于平衡时单纯的热运动速率增长了多大的比例。

3.我们来看分子${\sigma }_n{\sigma }_p{N}_t(p_n{n}_n-n_i^2)$
我们以一个班级的同学将教室中的多余椅子搬到室外，这样一个情境来打比方。比如说教室只有20个座位，但是却有50张椅子，因此这20个同学就需要把30张椅子搬出去。

复合中心浓度$N_t$就相当于班级里的同学人数20。人数越多，则搬椅子的速度也就越快。

但椅子不是立刻就可以搬走的，它需要每个同学去找到对应的椅子，然后再搬。而电子俘获截面${\sigma }_n$和空穴俘获截面${\sigma }_p$的乘积越大，则每个学生找到自己要搬的椅子就越快。因此，电子复合截面与空穴复合截面两者的乘积${\sigma }_n\cdot {\sigma }_p$越大，则多子和少子就越容易被负荷中心所捕获，然后进行复合。（其实电子俘获截面我也没比喻得很透彻，粗略地看一下吧）

4.多子、少子浓度之积与本征载流子浓度的平方之差$p_n{n}_n-n_i^2$，可以理解成总共需要搬多少张椅子。在这个例子中，就是30张椅子。

当教室有30张椅子的时候，大家都很容易找到椅子再搬出去，因此，所有的同学都被动员了起来。但是当教室中只有10张椅子的时候，就有一半的同学找不到需要搬的椅子，就会闲下来，速度就自然降低了。

5.如果分子这部分已经理解了，那么接下来我们来看分母${\sigma }_p[p_n+n_{i}exp(\frac{E_i-E_t}{kT}]+{\sigma }_n[n_n+n_{i}exp(\frac{E_t-E_i}{kT})]$

同样以班级同学搬椅子为例。在复合率的表达式中位于分母，就意味着其中的各项参数越大，搬椅子就越慢。

可以看出，分母是一个关于复合中心能级位置$E_t$的表达式。复合中心能级位置与本征费米能级的差值越大，则分母的两项中的某一项就会显得非常大。
你可以理解成能级位置的大小与椅子的重量地位相同。椅子越重，则搬的越慢。

这个式子太复杂了，因此我们通过约算，用过剩的少子寿命${\tau }_p$来表示复合率，得到：$U\approx \frac{p_n-p_n}{{\tau }_p}$
此时的过剩少子寿命${\tau }_p$由复合中心的能级位置$E_t$决定

表面复合

表面复合的定义：通过半导体表面态进行的复合现象

表面复合规律的定义：在表面上，单位面积及单位时间内载流子复合的总数可以沿用间接复合中复合率的表达式：$U=v_{th}\cdot \frac{{\sigma }_n{\sigma }_p{N}_t(p_n{n}_n-n_i^2)}{{\sigma }_p[p_n+n_{i}exp(\frac{E_i-E_t}{kT})]+{\sigma }_n[n_n+n_{i}exp(\frac{E_t-E_i}{kT})]}$

表面复合的产生原因：由表面悬挂键产生表面态的能态，这将增加在表面的复合率。

表面符合率的运算依旧太过复杂。在小注入状态，且在表面电子浓度等于本体内多子浓度时，可以简化得到：$U\approx v_{th}{\sigma }_p{N}_{st}(p_s-p_{n0})$
表面区域复合中心的浓度$N_{st}$来源于复合中心浓度$N_t$，添加的"s"指表面区域（surface）

由于$v_{th}{\sigma }_p{N}_{st}$的单位为$cm\cdot s^{-1}$，所以我们引入小注入表面复合速度这个变量，符号表示为$S_{lr}$:$S_{lr}=v_{th}{\sigma }_p{N}_{st}$

表面复合的作用：表面复合将导致受光照时，半导体侧表面具有较低载流子浓度。
这个较低的载流子浓度到底会有多低呢？此时的表面载流子浓度大概趋近于热平衡值。
降低的这部分载入子浓度的梯度，就产生了表面复合电流的扩散电流密度。

可以看到，最后我强调了一下小注入，是因为当载流子浓度变得越来越高时，会出现其他特别的现象，其中一个就是俄歇过程。

俄歇过程

俄歇过程的定义：俄歇复合过程时电子-空穴复合时将动量或能量转移给第三个粒子的过程。俄歇过程是一种三粒子效应，过程涉及电子、空穴和另外一个吸收能量的载流子。
俄歇过程的定量描述：$R_{Aug}=B{n}^{2}p或B{p}^{2}n$
式中的$B$受温度影响较大

连续性方程

连续性方程式的定义：描述半导体中漂移、扩散、复合同时发生的总体效应方程

连续方程式的定量描述：$\frac{\partial n}{\partial t}Adx=[\frac{J_n(x)A}{-q}-\frac{J_n(x+dx)A}{-q}]+(G_n-R_n)Adx$
$\frac{\partial n}{\partial t}Adx$表示宽$dx$,截面积为$A$的小长方块中电子增加的速率；
$\frac{J_n(x)A}{-q}$为x处流入小长方块的电子数目，电荷量q前的符号，是因为电子带负电；
$\frac{J_n(x+dx)A}{-q}$为$(x+dx)$处流出小长方块的电子数目；
小长方块内电子产生的速率$G_{n}Adx$；
小长方块内电子空穴对的复合率$R_{n}Adx$

对上面这个复杂公式进行化简约分，得到电子的基本连续性方程：$\frac{\partial n}{\partial t}=\frac{1}{q}\cdot \frac{\partial J_n}{\partial x}+(G_n-R_n)$
空穴的基本连续性方程为：$\frac{\partial p}{\partial t}=\frac{1}{q}\cdot \frac{\partial J_p}{\partial x}+(G_p-R_p)$
由电子和空穴的基本连续性方程，可以知道：在这样一个极薄（宽为$dx$的半导体方块中，其载流子浓度增加的速率等于电流密度增加的速率与电荷的商，再加上产生速率和复合速率之差

计算“电流密度与电荷的商”的目的可以理解为是为了去除载流子电荷量的影响，直接观察载流子在导体内的移动数量。

如果说"电流密度与电荷的商"是半导体中已有的、由于外加电场影响所增加的载流子；那么产生速率和复合速率之差，则是除电压以外，诸如光激发等其他激发形式所增加的那部分载流子浓度。

将$\{\begin{array}{l}{J}_n=q{\mu }_{n}nE+q{D}_n\frac{dn}{dx}\\ J_p=q{\mu }_{p}pE-q{D}_p\frac{dp}{dx}\\ U=\frac{p_n-p_{n0}}{{\tau }_p}\end{array}$代入入基本连续性方程，可以得到在一维的小注入情形下少子的连续性方程：图片:

泊松方程式

泊松方程式的定量描述：$\frac{dE}{dx}=\frac{{\rho }_s}{{\epsilon }_s}$
表面介电常数${\epsilon }_s$；
空间电荷密度${\rho }_s$的定义：带电载流子浓度和电离杂质浓度的代数和。并且以空穴浓度和施主浓度为正，电子浓度和受主浓度为负
空间电荷密度:${\rho }_s=q(p-n+N_D^{+}-N_A^{-})$
由空间内和密度的表达式可以知道，载流子的浓度需要与其对应的提供者——施主和受主杂质浓度相减。因此在正常情况下，在空间电荷密度应该为0

从高中物理中，我们可以知道：如果在均匀电场中，两极板之间的距离x乘以均匀的电场强度E，可以得到电势$\psi$。相反地，如果对电势作关于距离的微分，则也可以得到电场强度。

利用大学中学到的微积分，可以同样得到这一点。因此，我们将电场强度和电势差的微积分关系，和空间电荷密度的表达式${\rho }_s=q(p-n+N_D^{+}-N_A^{-}$代入，可以得到更加完整的泊松方程式：$\frac{d^2\psi }{d{x}^2}=\frac{dE}{dx}=\frac{{\rho }_s}{{\epsilon }_s}=\frac{q(p-n+N_D^{+}-N_A^{-})}{{\epsilon }_s}$

单边稳态注入

单边稳态注入时，令N型半导体边界处的少子（即空穴）的浓度为$p_n(x=0)=p(0)$
N型半导体往内延伸至大约为无限深度的位置，得到少子的浓度为$p_n(x\to \propto )=p_{n0}$
当x在0到正无穷之间时，根据三要素公式，少子的浓度表达式为：$p_n(x)=p_n(x\to \propto )+[p_n(x=0)-p_n(x\to \propto )]exp(-\frac{x}{L_p})$
对上式进行简化，得到：
$p_n(x)=p_{n0}+[p(0)-p_{n0}]exp(-\frac{x}{L_p})$
其中$L_p$为扩散长度。$L_p=\sqrt{扩散系数D_p\cdot 过剩少子寿命{\tau }_p}$

热电子发射过程

热电子发射过程，也称为热离化发射过程。对n型半导体而言，其产生条件为：电子能量超过电子亲和势$qx$，即当一个电子的能量超过qx时，它就可以被热离化发射至真空能级。

电子亲和势$qx$的定义：导带底边缘与真空能级的能量差
功率(函)数$q{\varphi }_s$的定义：本征费米能级$E_i$与真空能级的能量差

知道这两个定义之后，如何计算有多少电子可以热离化呢？

由热离化发射过程的定义可以知道，我们要计算可以热离化的电子浓度，相当于计算能量高于电子亲和势的电子浓度。

由此得到热离化电子的浓度为：$n_{th}={\int }_{qx}^{\propto }n(E)dE=N_c\cdot exp[-\frac{q(x+v_n)}{kT}]$
导带有效态密度$N_c$;导带底$E_c$与本征费米能级$E_i$的差值$V_n$，本质上是一个电势差。

隧穿过程

隧穿过程的定义：势垒高$q{V}_0$等于电子亲和势$qx$。当两个隔离的半导体距离$d$足够小时，一边的电子即使能量小于势垒高，也能完成跨势垒($q{V}_0$)输运，并移到另一边的过程。

强电场效应

强电场效应的现象（假设平均自由时间${\tau }_c$与$E$无关）：电场强度$E$较低时，漂移速度$v_n,v_p$也较低，电场强度与漂移速度近似呈线性关系；电场强度$E$渐渐增加时，漂移速度也增加。当漂移速度趋近于热速度时，漂移速度与电场强度将不再成近似线性关系，增速趋缓；电场强度继续增大，漂移速度趋近于饱和速度$v_s$。

我们对强电场效应的现象做定量的描述，可以得到漂移速度$v_n或v_p$和电场强度$E$、饱和速度$v_s$之间的近似关系：$v_n,v_p=[\frac{v_s}{1+(E_0+E{)}^y}{]}^{\frac{1}{y}}$
硅材料在温度为300k时的饱和速度$v_s=10^{7}cm\cdot s^{-1}$

电子的常数$E_0$为：$E_0=7\cdot 10^{3}V\cdot c{m}^{-1}$
空穴的常数$E_0$为：$E_0=2\cdot 10^{4}V\cdot c{m}^{-1}$
电子的常数$y=2$
空穴的常数$y=1$

GaAs的强电场效应

GaAs的强电场效应一般应用于微波转移器件，其现象为：两种载流子的漂移速度$v_n,v_p$先随电场强度$E$增加，达到极大值后反而逐渐下降的现象。

强电场效应产生的原因：GaAs的能带结构允许电子从高迁移率$\mu$的“谷”跃迁至低迁移率但能量较高的临近“谷”中。

谷的定义：能带图中，能量极小值点或最小值点。

雪崩过程

雪崩过程的条件：有足够强的电场，使电子在晶格碰撞前获得极大动能。

雪崩过程的现象：从强电场中，电子获得极大动能；大动能的电子在晶格碰撞中使被碰撞原子或分子的键断裂，因而产生新的电子-空穴对；产生的电子-空穴对不断重复“获得动能、晶格碰撞、键断裂、生成电子-空穴对”的过程，这样的一种现象。雪崩现象将导致p-n结的结击穿。

电离率ionization rate

电离率的定义：一个电子经过单位距离所产生的电子-空穴对数目，称为电子的电离率${\alpha }_n$；同样，${\alpha }_p$为空穴的电离率。
硅在大于$3\times 10^{5}V/cm$的电场下，砷化镓在大于$4\times 10^{5}V/cm$的电场下，由雪崩过程造成的电子-空穴对产生速率G为：$G_A=\frac{1}{q}({\alpha }_n|J_n|+{\alpha }_p|J_p|)$
其中$J_n,J_p$分别为电子及空穴电流密度。此表示法可使用于器件工作在雪崩
情况下的连续性方程式

习题

例1:计算在300K下，一迁移率为$1000c{m}^2/(V\cdot s)$的电子的平均自由时间和平均自由程。设$m_n=0.26m_0$
需要用到的公式包括1.迁移率的计算公式$\frac{{\mu }_n}{q}=\frac{{\tau }_c}{m_n}$ 2.能量均分理论得到的电子动能表达式$\frac{1}{2}{m}_n{v}_{th}^2=\frac{3}{2}kT$
3.平均自由程的计算式$l_{th}=v_{th}\ast {\tau }_c$ 4.$m_0=0.91\times 10^{-30}$ 5.$q=1.6\times 10^9$ 5.室温$kt=0.026eV，kt/q=0.026V$

例2:一n型硅晶掺入每立方厘米$10^{1}6$个磷原子，求其在室温下的电阻率。

需要使用到的公式包括1.浅掺杂能级下的完全电离 2.电导率公式$\sigma =\frac{J}{E}=q(n{\mu }_n+p{\mu }_p)$ 3.电导率与电阻率的关系式

例3:一硅晶样品掺入每立方厘米$10^{16}$个磷原子，若样品的$W=500\mu m,A=2.5\times 10^{-3}c{m}^2,I=1mA,B_Z=10^{-4}Wb/c{m}^2$，求其霍耳电压。
需要用到的公式包括：1.n型半导体霍尔系数的表达式$R_H=-\frac{1}{np}$ 2.霍尔电压的计算公式$E_y=\frac{V_H}{W}$；$p==\frac{J_p{B}_z}{q{E}_y}=\frac{\frac{I}{A}{B}_Z}{q\frac{V_H}{W}}=\frac{I{B}_{z}W}{q{V}_{H}A}$

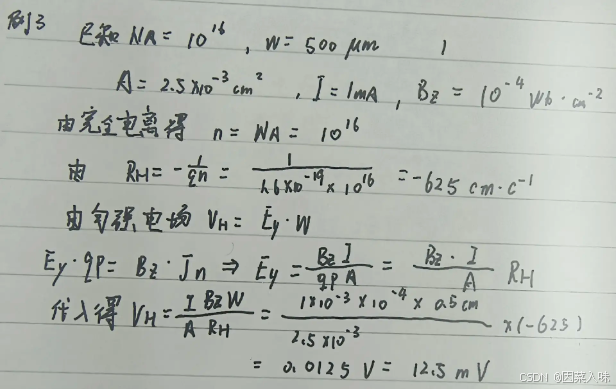
例4:假设T=300K， 一个n型半导体中，电子浓度在0.1cm的距离中从$1\times 10^{18}c{m}^{-3}$至$7\times 10^{17}c{m}^3$作线性变化，计算扩散电流密度。假设电子扩散系数D_n=22.5cm^2/s。
需要用到的公式包括：1.扩散电流密度的计算公式电子扩散电流密度：$J_n=-qF=q{D}_n\frac{dn}{dx}$；总电流密度$J_n=q{\mu }_{n}E+q{D}_n\frac{dn}{dx}$

例5:室温下少数载流子(空穴)于某一点注入一个均匀的n型半导体中，施加一个50V/cm的电场于其样品上，且电场在100us内将这些少数载流子移动了1cm。求少数载流子的漂移速率及扩散系数。
需要用到的公式包括1.漂移速度与路程、时间的关系 2.迁移率的计算式 3.爱因斯坦关系式$\frac{D_n}{kT}=\frac{{\mu }_n}{q}$

例6:光照射在一个$n_{n0}=10^{14}c{m}^{-3}$的砷化镓样品.上，且每微秒产生电子-空穴对$10^{13}/c{m}^3$。若${\tau }_n={\tau }_p=2{\mu }_s$， 求少数载流子浓度的变化。
需要用到的公式包括1.本征半导体浓度与其他半导体浓度的关系式 2.复合过程中少子浓度的计算式$p_n=p_{n0}+{\tau }_{p}U$ 3.对硅$n_i=9.65\times 10^{9}c{m}^{-3}$

例8:一n型硅，具有电子亲和力$qx=4.05eV$及$q{V}_n=0.2eV$，计算出室温下被热离化发射的电子浓度$n_{th}$。假如我们将等效的qx降至0.6eV，$n_{th}$为多少?
需要用到的公式包括1.热离化电子浓度的计算式 2.对硅$Nc=2.86\times 10^{19}c{m}^{-3}$