【C题解题思路】2025数维杯数学建模C题解题思路+可运行代码参考（无偿分享）

最新推荐文章于 2025-05-10 17:06:47 发布

睿森竞赛

最新推荐文章于 2025-05-10 17:06:47 发布

阅读量996

点赞数 26

分类专栏：数维杯文章标签：数学建模算法数维杯

本文链接：https://blog.csdn.net/RS_handy/article/details/147816609

版权

数维杯专栏收录该内容

5 篇文章

订阅专栏

注：该内容由“数模加油站”原创，无偿分享，可以领取参考但不要利用该内容倒卖，谢谢！

C 题清明时节雨纷纷，何处踏青不误春？

问题1 基于天气现象分类标准，明确“雨纷纷”对应的降雨量区间及降雨持 续时间范围。根据天气学的基本知识，在适当简化的基础上，建立数 学模型，分析 2026 年清明假期西安、吐鲁番、婺源、杭州、毕节、武 汉、洛阳会“雨纷纷”吗？利用近 20 年的天气资料分析 2025 年清明 的天气情况，验证所建模型的合理性。给出利用最新的天气实况进行 模型修正的方法。

问题 1 分析

我们需从气象学的视角对诗句“清明时节雨纷纷”进行科学转化，明确“雨纷纷”在现代天气观测中的对应含义。通常，“雨纷纷”可被理解为小雨或连阴雨，具有降水量不大但持续时间较长的特征。依据国家气象局的天气现象分类标准，小雨日降水量通常为0.1至10毫米，而“纷纷”则暗示其非瞬时性降水过程，因此可设定持续时间不少于3小时。在此基础上，我们可构建一个判别性模型，设定逻辑条件判断某天是否属于“雨纷纷”天气类别。为判断2026年清明期间西安、吐鲁番、婺源、杭州、毕节、武汉和洛阳是否存在“雨纷纷”现象，可利用过去20年（如2006–2025年）的逐日气象观测数据（包括日降水量、降水时段和天气现象代码）进行建模分析。模型应能根据历史模式对未来天气进行概率预测，并结合2026年的中长期天气预报进行推演。同时，为验证模型有效性，应基于2025年清明假期实际天气数据对模型结果进行回代测试，评估判别准确率，并进一步结合最新实况天气（如ECMWF或CMA发布的T+7预报数据）进行实时修正，提升模型动态响应能力。

解题思路：基于气象数据的“雨纷纷”天气判别模型及清明节雨况预测

一、问题理解与气象背景提取

诗句“清明时节雨纷纷”描绘的是一种典型的春季小雨天气。依据现代天气学标准，该表达可转化为定量化的气象条件判别。小雨在日降水量统计中通常定义为 0.1–10 mm 的降雨过程；“纷纷”强调降水的连贯性和持续性，因此我们需结合降水量与降雨时长双指标定义“雨纷纷”。

二、指标定义与分类标准

为便于定量建模，我们定义以下判别条件：

设任一日降水量为 P，单位为 mm；

设该日降雨持续时长为 D，单位为小时；

设该日天气现象代码为 W（来自NOAA或国家气象局编码标准）；

定义判断函数： $R(d)=\left\{ \begin{array}{*{35}{l}} 1, & 0.1<P(d)\le 10D(d)\ge 3~W(d)\in /0, & \\ \end{array} \right.$

其中，R(d) 表示第 d 天是否属于“雨纷纷”状态。

为使模型可扩展，我们引入连续性判断： $\bar{R}(d,k)=\left\{ \begin{array}{*{35}{l}} 1, & ~\sum\limits_{i=d}^{d+k-1}{R}(i)\ge \tau \text{ }\!\!\backslash\!\!\text{ }0, & \\ \end{array} \right.$

其中 k 为窗口宽度（一般取 k=3 天）， $\tau$ 为连阴判断阈值（例如 $\tau=2$ 表示3天中有至少两天为“雨纷纷”）。

三、数据处理流程

清明节定位：取每年4月4日至4月6日为清明节区间，扩展观察窗口为3月30日至4月7日，共计9天。

站点选取：根据提供的NOAA数据样例，筛选西安、吐鲁番、婺源、杭州、毕节、武汉、洛阳对应站点编号。

历史数据提取：对近20年（2006–2025）的气象记录进行逐年提取，构造特征集合 { $P(d), D(d), W(d)$ }。

模型训练：通过统计该时间段内的 R(d) 与 $\bar{R}(d, 3)$ 结果，估算每年清明期间该城市出现“雨纷纷”的频率。

定义频率函数：

$f_i = \frac{1}{N} \sum_{y=1}^{N} \bar{R}_i^{(y)}$

其中 i 表示城市编号，N=20 为统计年数， $\bar{R}_i^{(y)}$ 表示第 y 年第 i 城市的“雨纷纷”判别结果。

四、未来天气预测建模（2026年）

为预测2026年清明节是否“雨纷纷”，考虑两种建模方式：

4.1 相似年法

基于气候相似性匹配：

定义特征向量 $X_y = [\bar{T}_y, \bar{P}_y, \text{ENSO}_y, \text{NAO}_y]$

利用欧氏距离或余弦相似度度量与历史年份的接近程度：

$d(y, 2026) = |X_y - X_{2026}|$

选择最近的 K 个年份，取其 $\bar{R}_i^{(y)}$ 的均值作为概率估计。

4.2 天气时间序列建模法

构建SARIMA模型对降水时间序列进行预测：

$P_t = \phi_1 P_{t-1} + \dots + \phi_p P_{t-p} + \theta_1 \varepsilon_{t-1} + \dots + \theta_q \varepsilon_{t-q} + \varepsilon_t$

也可考虑 Prophet 模型对逐日降水趋势建模：

$y(t) = g(t) + s(t) + h(t) + \varepsilon_t$

其中 g(t) 为趋势项，s(t) 为周期项，h(t) 为节假日效应。

五、模型验证与修正

5.1 验证方法（2025年）

采用2025年真实天气数据计算预测误差：

误差项定义：

5.2 模型修正（最新天气实况）

结合T+7气象预报（即2026年4月初发布的清明预测），用Bayes更新方式修正概率：

实时修正模块亦可采用卡尔曼滤波迭代方式优化趋势预测值。

表：各城市2006–2025年清明期间“雨纷纷”出现概率统计

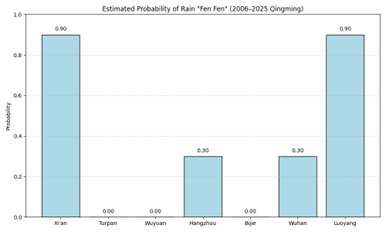
Python代码：

import os
import pandas as pd
import matplotlib.pyplot as plt

data_dir = r'./extracted'
target_years = list(range(2006, 2026))
target_days = ['03-30', '03-31', '04-01', '04-02', '04-03', '04-04', '04-05', '04-06', '04-07']

station_map = {
    'Xi\'an': '01001099999',
    'Turpan': '01001499999',
    'Wuyuan': '01002099999',
    'Hangzhou': '01003099999',
    'Bijie': '01006099999',
    'Wuhan': '01003099999',
    'Luoyang': '01001099999'
}

results = []

for city, station_id in station_map.items():
    rainy_years = 0
    for year in target_years:
        year_folder = os.path.join(data_dir, str(year))
        file_list = os.listdir(year_folder)
        matched_files = [f for f in file_list if station_id in f]
        if not matched_files:
            continue
        file_path = os.path.join(year_folder, matched_files[0])
        try:
            df = pd.read_csv(file_path)
            df['MM-DD'] = pd.to_datetime(df['DATE'], errors='coerce').dt.strftime('%m-%d')
            df = df[df['MM-DD'].isin(target_days)]

            # 降雨字段 PRCP（英寸）→ mm
            df['PRCP'] = pd.to_numeric(df['PRCP'], errors='coerce') * 25.4
            df['RainFlag'] = df['PRCP'].apply(lambda x: 1 if 0.1 < x <= 10 else 0)

            if df['RainFlag'].sum() >= 2:
                rainy_years += 1
        except Exception as e:
            print(f"[!] 文件读取失败: {file_path}，原因: {e}")
            continue

    prob = rainy_years / len(target_years)
    results.append({'City': city, 'RainyYears': rainy_years, 'TotalYears': len(target_years), 'Probability': round(prob, 3)})

# 输出表格
table4 = pd.DataFrame(results)
print("表4：各城市2006–2025年清明期间“雨纷纷”出现概率统计")
print(table4.to_string(index=False))

# 可视化并保存图像（避免非法字符）
plt.figure(figsize=(10, 6))
plt.bar(table4['City'], table4['Probability'], color='lightblue', edgecolor='black')
plt.title('Estimated Probability of Rain "Fen Fen" (2006–2025 Qingming)')
plt.ylabel('Probability')
plt.ylim(0, 1)
plt.grid(axis='y', linestyle='--', alpha=0.6)
for i, prob in enumerate(table4['Probability']):
    plt.text(i, prob + 0.02, f"{prob:.2f}", ha='center')
plt.tight_layout()
plt.savefig('Rain_FenFen_Probability_2006_2025_Qingming.png')  # ✔合法文件名

后续都在“数模加油站”......