误差模型
来源:
- 零飘随机游走
- 三轴不绝对垂直
- 白噪声
- 三轴测量灵敏度不一
坐标系建立
加速度计:
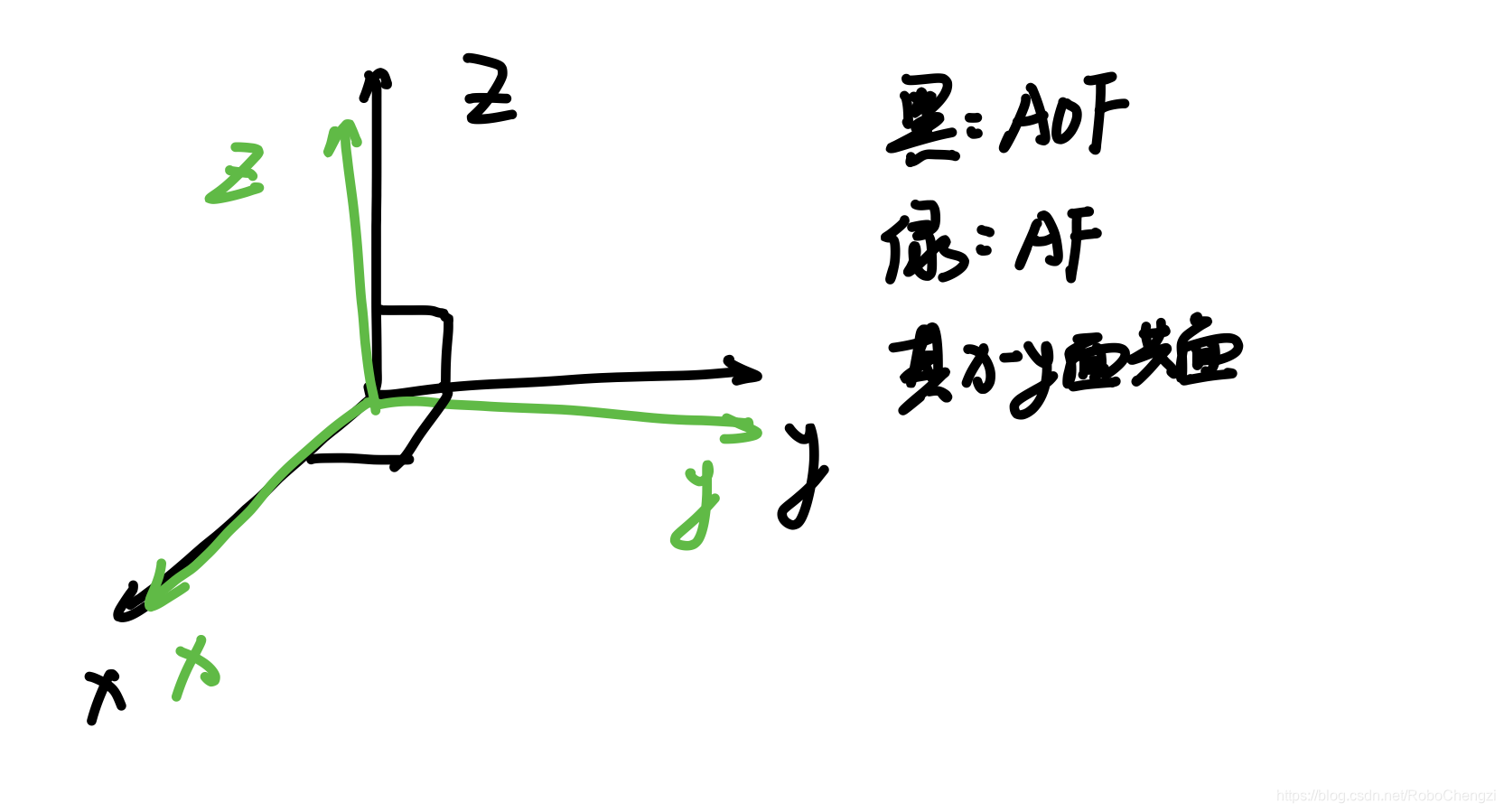
- 原始传感器坐标:AF(不正交)
- 正交传感器坐标:AOF
AOF确定规则
- x轴AOF和AF相同
- y轴AOF在AF的x,y构成的平面内
- z轴为x,y叉乘
陀螺仪:
- 原始传感器坐标:GF(不正交)
- 正交传感器坐标:GOF
载体坐标系:BF=AOF
误差模型确定
三轴不垂直
对于小角度的不垂直,可采用如下的表达(参考文献18)
s
B
=
T
s
S
T
=
[
1
−
β
y
z
β
z
y
β
x
z
1
−
β
z
x
−
β
x
y
β
y
x
1
]
s^{B} = Ts^{S} \\ T=\left[\begin{array}{c c c} 1 & -\beta_{yz} &\beta_{zy}\\ \beta_{xz} & 1 &-\beta_{zx}\\ -\beta_{xy}& \beta_{yx} &1\\ \end{array}\right]
sB=TsST=⎣⎡1βxz−βxy−βyz1βyxβzy−βzx1⎦⎤
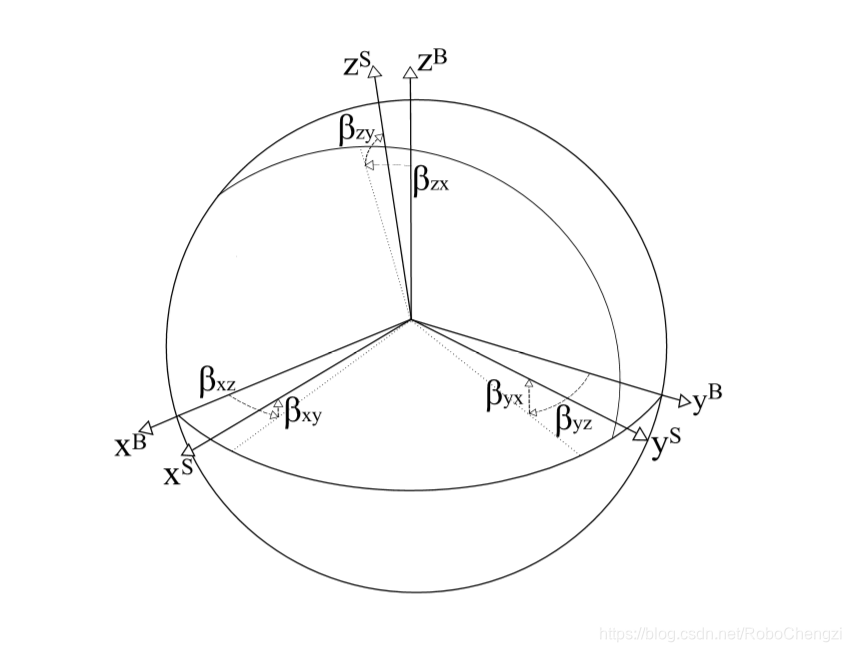
其中S坐标系为非正交坐标系,B坐标系为正交坐标系,而T中各参数如图为轴间角度偏差。
尺度误差
由于敏感度不一致,实际值和真实值的比例。
K
=
[
s
x
0
0
0
s
y
0
0
0
s
z
]
K = \left[\begin{array}{c c c} s_x & 0 &0\\ 0 & s_y &0\\ 0& 0 & s_z\\ \end{array}\right]
K=⎣⎡sx000sy000sz⎦⎤
零偏
b = [ b x b y b z ] b=\left[\begin{array}{c } b_x \\ b_y \\ b_z \\ \end{array}\right] b=⎣⎡bxbybz⎦⎤
最终的误差模型
加速度计:
a
O
=
T
a
K
a
(
a
S
+
b
a
+
v
a
)
a^O = T^aK^a(a^S+b^a+v^a)
aO=TaKa(aS+ba+va)
陀螺仪:
g
O
=
T
g
K
g
(
g
S
+
b
g
+
v
g
)
g^O = T^gK^g(g^S+b^g+v^g)
gO=TgKg(gS+bg+vg)
其中
v
a
,
v
g
v^a,v^g
va,vg为高斯白噪声。
矫正算法原理
先估计加速度计的参数,再用矫正好的加速度计去估计陀螺仪的参数
加速度计
需要估计的参数:
θ
a
c
c
=
[
α
y
z
α
z
y
α
z
x
s
x
a
s
y
a
s
z
a
b
x
a
b
y
a
b
z
a
]
\theta^{acc}=\left[\begin{array}{c} \alpha_{yz} & \alpha_{zy} & \alpha_{zx} & s_x^a & s_y^a & s_z^a & b_x^a & b_y^a & b_z^a \end{array}\right]
θacc=[αyzαzyαzxsxasyaszabxabyabza]
注意:由于载体坐标系(BF)和加速度计的正交系(AOF)重合,
α
x
y
,
α
y
x
,
α
x
z
=
=
0
\alpha_{xy},\alpha_{yx},\alpha_{xz}==0
αxy,αyx,αxz==0,因此参数要少一些。
主要思路 :
利用重力的模长不变,利用最小二乘法估计参数使得每次静止时的重力模长都尽量接近真实重力大小。
误差函数:
L
(
θ
a
c
c
)
=
∑
k
−
1
M
(
∣
∣
g
∣
∣
2
−
∣
∣
h
(
a
k
s
,
θ
a
c
c
)
∣
∣
2
)
2
L(\theta^{acc}) = \sum_{k-1}^{M}(||g||^2-||h(a_k^s,\theta^{acc})||^2)^2
L(θacc)=k−1∑M(∣∣g∣∣2−∣∣h(aks,θacc)∣∣2)2
其中
g
g
g为重力加速度,
a
k
s
a_k^s
aks为直接测量的加速度计值,
θ
a
c
c
\theta^{acc}
θacc为待估计的参数,函数
h
(
a
k
s
,
θ
a
c
c
)
=
T
a
K
a
(
a
S
+
b
a
)
h(a_k^s,\theta^{acc})= T^aK^a(a^S+b^a)
h(aks,θacc)=TaKa(aS+ba)
然后非线性最小二乘求解参数,如LM算法。
陀螺仪
需要估计的参数:
θ
g
y
r
o
=
[
γ
y
z
γ
z
y
γ
x
z
γ
z
x
γ
x
y
γ
y
x
s
x
a
s
y
a
s
z
a
]
\theta^{gyro}=\left[\begin{array}{c} \gamma_{yz} & \gamma_{zy} & \gamma_{xz} & \gamma_{zx} & \gamma_{xy} & \gamma_{yx} &s_x^a & s_y^a & s_z^a \end{array}\right]
θgyro=[γyzγzyγxzγzxγxyγyxsxasyasza]
注意:没有估计bias
主要思路 :
利用重力方向不变。初始状态时记录重力方向后旋转一定角度后静止,采用陀螺仪积分计算预估旋转后的重力方向,此外采用加速度计计算真实的重力方向。采用非线性最小二乘的方法不断的优化参数,使得二者差值最小。
误差函数:
L
(
θ
g
y
r
o
)
=
∑
k
=
2
M
(
u
a
,
k
−
u
g
,
k
)
2
L(\theta^{gyro}) = \sum_{k=2}^{M}(u_{a,k}-u_{g,k})^2
L(θgyro)=k=2∑M(ua,k−ug,k)2
其中
u
a
,
k
,
u
g
,
k
u_{a,k},u_{g,k}
ua,k,ug,k分别为陀螺仪预估重力方向与加速度计实测方向。
矫正算法流程
静止检测
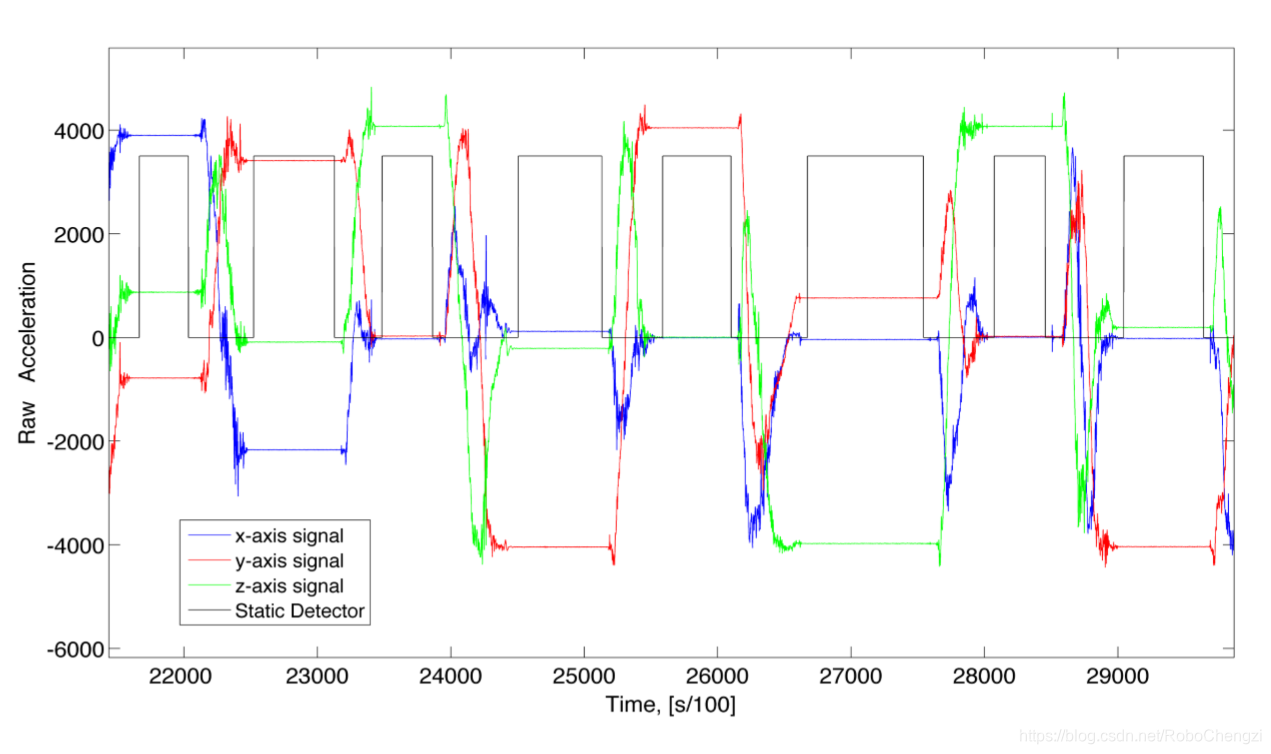
检测加速度计在前2s内的方差,若方差小于一定值则认为是静止的,黑线部分是静止标志位,其判断函数为:
s
(
t
)
=
[
v
a
r
(
a
x
t
)
]
2
+
[
v
a
r
(
a
y
t
)
]
2
+
[
v
a
r
(
a
z
t
)
]
2
s(t) = \sqrt{[var(a_x^t)]^2+[var(a_y^t)]^2+[var(a_z^t)]^2}
s(t)=[var(axt)]2+[var(ayt)]2+[var(azt)]2
龙格-库塔积分
四元数积分的一种方法,精度要比直接加要高一些,论文中采用的是四阶龙格-库达积分,可详细去看相关文章。
艾伦方差
初始时静止一段时间计算艾伦方差,具体计算论文未详细说明,主要就是得到了对bias及其方差的估计。
算法操作流程
首先静止 T w a i t T_{wait} Twait时间,估计艾伦方差。然后选择一定角度后静止,不断重复这一过程,进行约36~50次,以保证参数的可观,并保证每次静止时间在1-4s。最后调用算法进行矫正。























 2869
2869











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








