一、背景
人们已经发现,将神经网络和微分方程结合起来是可能的。
首先介绍一种开创性的神经常微分方程(神经ODE)研究工作:考虑图1(a)中的一般架构,是学习近似的神经网络,其中h(t)是层(或时间)t上的隐藏向量。因此,神经网络由ODE系统描述,每个ODE系统描述一个隐藏元素的动态。
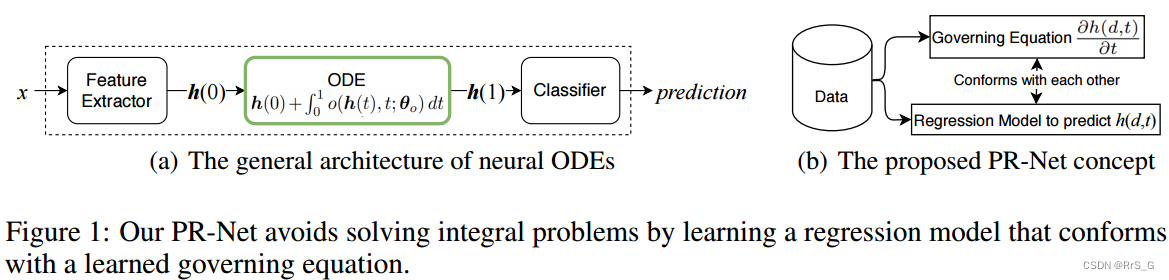
虽然神经ode有许多首选特征,但它们也有以下限制:(1)、神经ode可以将t解释为连续变量,我们可以在任意层(或时间)l有隐藏向量 ,其中
是一个以
为参数的神经网络。(2)、神经ode有时比其他传统的神经网络设计具有更少的参数。(3)、神经ode的前向传递推断在解决积分问题时可能会花费很长时间。为了提高推断时间,已经提出了多种对策,但解决积分问题是不可避免的。
为了解决这一局限性,本文提出了偏微分方程(PDE)-正则化神经网络(PR-Net)的概念,以直接学习一个隐藏元素,表示层(或时间)t∈[0,T]和维数d∈R^m的h(d, t)。在一般情况下,PDE由(1)t = 0时的初始条件。(2)空间域R^m的边界位置的边界条件。(3)描述的控制方程。因此,从数据中学习偏微分方程可以简化为一个预测满足初始/边界条件和控制方程的h(d, t)的回归问题。
在训练PR-Net时,h(0)是由早期的特征提取层提供的,这与神经ode相同。然而,对于下游的机器学习任务,一个合适的控制方程是未知的。因此,本文提出训练一个回归模型,同时预测h(d, t)及其控制方程(见图1(b)),而神经ode只直接学习控制方程(即)。这种方法的主要优点是,我们可以消除解决积分问题的必要性;在神经ode中,我们只学习一个控制方程,解决积分问题是必须的。
与以前的方法相比,本文的方法有不同的功能,同时解决连续变量t的正问题和反问题。由于这种独特的特性,该方法可以应用于下游通用机器学习任务,我们没有先验知识在控制方程,比如图像分类。我们的网络PR-NET有以下特点:(1)、PR-Net训练一个回归模型,输出标量元素h(d, t)(不解决任何积分问题),我们可以把d和t都考虑为连续变量。因此,可以在任意维数和层数上构造灵活的隐藏向量。(2)、PR-Net不用解决积分问题,而神经ode需要解决积分问题。(3)、通过学习控制方程,我们可以对PR-Net的整体行为进行规范化。实验表明,这大大提高了模型的鲁棒性。
二、偏微分方程
首先在介绍一般情况下偏微分方程的正问题和反问题(见表1)。

2.1、一般情况下偏微分方程的正问题
正问题即给定初始条件,边界条件
和控制方程g的情况下寻找解
,其中空间域:
,时间域:
,
是空间域的边界位置。控制方程通常是如下形式:
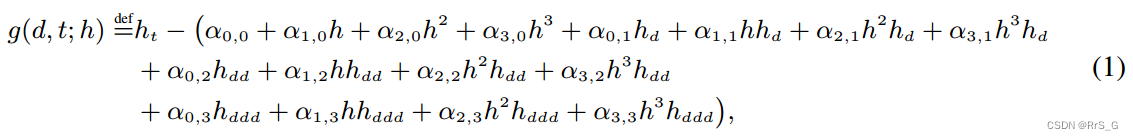
其中g(d, t; h) = 0。
接下来就是用一个神经网络近似解
。
2.2、一般情况下偏微分方程反问题
反问题即在给定初始条件,解函数
的条件下寻找控制方程。它通过以下损失学习等式(1)中的
:
三、PR-net
本文工作的目标是用PDE替换ode系统(参见图[1(a))。假设一个特定于目标任务的PDE先验已知,给定特征提取器从样本x中提取的初始条件h(0),可以通过2.1节描述的方法求解正向问题。然而,一个特定于目标任务的PDE通常是不已知的,因此,控制方程应该通过解决反问题被学习。但是,通常情况下解函数h(d, t)也不是已知的。因此,假设控制方程包含最常见的偏导数项,即等式(1),然后提出交替求解正反问题:固定控制方程g(更准确的说是)去训练θ,固定θ去训练
。
3.1、解决正问题
本文通过2.1节中的方法设置如下:(1)、添加一个特定任务的损失,即对于图像分类的交叉熵损失。(2)、通过初始条件h(0)参数化神经网络f。(3)、去除边界条件。设f(h(0),d,t;θ)是在初始条件h(0)变化的情况下近似h(d, t)的神经网络。
该框架的关键好处是,对于f,可以通过查询h(d,t)提取任何隐藏元素,定义H是一组(d, t)对,我们构造隐藏向量将用于下游任务(如下图)。

用如下损失训练θ:
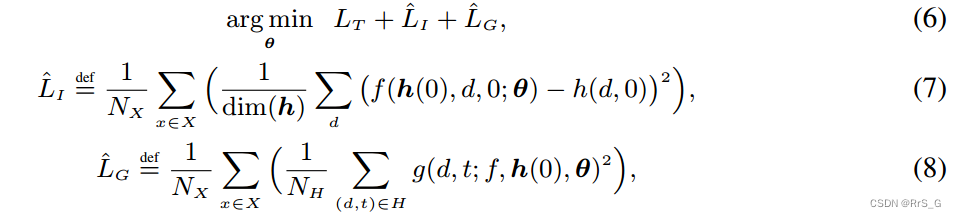
其中是特定任务的损失,X是训练集,
是训练样本的数量,
是
中元素的数量,即
。
通过用H中的(d, t)查询f(h(0),d,t;θ)去构造,有一点需要注意的是,为了更好地构造
,甚至可以对H中的对进行如下训练:
,因此,可以从不同的维度和层数收集
的元素。只使用
训练H,因为
最后会被送入分类器,应该可以很好地完成下游的任务。特征提取器和分类器也只用
进行训练。
3.2、解决反问题
固定θ后,通过如下损失优化:
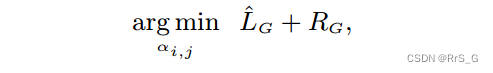
其中,最小化
的和,根据Occam’s razor得到一个稀疏控制方程,因为在许多偏微分方程中,它们的控制方程是稀疏的。这种优化使我们能够在许多可能的控制方程中选择最稀疏的解。因此,在许多情况下,我们的正则化逆问题是唯一解的。
3.3、训练算法
整体训练算法如图3所示。我们交替训练θ,(d,t)∈H,以及。
如果神经网络f是解析的或等价的一致Lipschitz连续的,那么训练θ的正问题就成为一个适定问题(即其解总是存在且唯一),许多神经网络算子是解析的,例如,softplus、全连接、指数等。因此,在这种神经网络的温和条件下,可以满足良好的适定性。
由于稀疏性的要求,反问题在许多情况下也可以唯一地解决。
因此,本文提出的训练算法可以收敛到一个合作均衡,注意θ,(d,t)∈H,以及协同使
最小。因此,本文提出的训练方法可以看作是一个合作博弈,如定理所示。

训练过程结束后,不再需要(因为θ此时已经符合学习到的控制方程),可以在测试时丢弃。
对于复杂的下游任务,应该提前完成训练(算法第5行)。然后,仔细更新PDE参数(第6行),其他训练程序紧随其后。算法1中的序列在本文的实验中产生了最好的结果。但是,对于其他数据集或下游任务,这个序列可以改变。





















 511
511











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








