【信号与系统】如何理解公式：r(t)=e(t)﹡h(t)

对于公式

首先我们需要知道它成立的前提条件是系统为线性时不变（LTI）系统

而对于LTI系统，它满足线性（叠加性、均匀性），时不变特性以及微分特性

1.线性：系统输入E1对应输出R1，输入E2对应输出R2；信号C1E1+C2E2输入系统后得到的输出为C1R1+C2R2

2.时不变特性：系统输入 E(t) 对应输出 R(t)，信号 E(t-t₀) 输入系统后得到的输出为 R(t-t₀)

3.微分特性：系统输入E对应输出R，信号E⁽ⁿ⁾输入系统后得到的输出为R⁽ⁿ⁾

---

对于卷积这种运算，它满足一条性质：任何信号和冲激信号相卷得到的都是该信号本身，即：

也即：

证明：

任意信号 f(t) 都可写成无数个矩形脉冲信号叠加的形式，而矩形脉冲可以用阶跃信号表示：例如 u(t) -u(t-T) 就表示一个宽度为T的矩形脉冲

故有如下等式：

令∆τ→0，即得：

得证。

---

由于系统输入单位冲激信号 δ(t) 时响应为 h(t)，根据LTI系统的特性有如下对应输入—输出关系

激励e(t)	响应r(t)
δ(t)	h(t)
δ(t-τ)	h(t-τ)
e(τ)∙δ(t-τ)	e(τ)∙h(t-τ)
∫ [e(τ)∙δ(t-τ)] dτ	∫ [e(τ)∙h(t-τ)] dτ

由于e(t)可表示为如下形式：

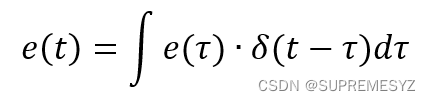
故输出r(t)为：

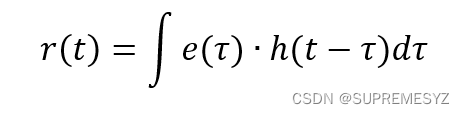
也即：